ММФ лекции / Матем.-3
.doc
КОНЕЧНОЗНАЧНЫЕ СИНГУЛЯРНЫЕ ФУНКЦИИ
Функция Хевисайда
При изучении распространения сигнала по проводам Оливер Хевисайд в конце XIX века ввел функцию включения
 (3.1)
(3.1)

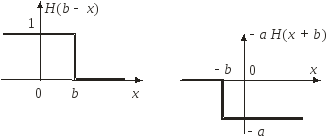
На
рисунках
![]() включается в точке
включается в точке
![]() ,
где
,
где
![]() .
При
.
При
![]() функция
функция
![]() ,
при
,
при
![]() функция
функция
![]() .
.
Из рисунков получаем
![]() .
(3.2)
.
(3.2)
Из нормировки дельта-функции следует
 ,
,
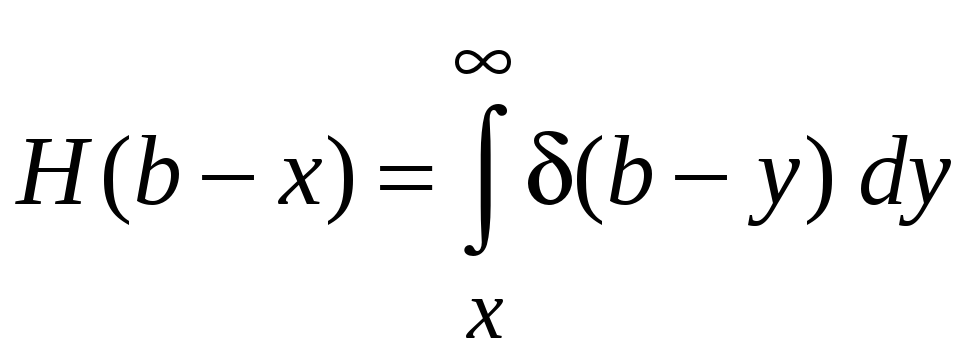 ,
,
тогда
![]() ,
,
![]() ,
(3.3)
,
(3.3)
где использовано дифференцирование интеграла по пределу
если
 ,
то
,
то
![]() ;
;
если
 ,
то
,
то
![]() .
.
Функция включения позволяет расширить пределы интегрирования. Из определения (3.1) получаем
 ,
,
 .
(3.4)
.
(3.4)
Свертку находим с учетом (3.4)
 .
(3.4а)
.
(3.4а)
В
(3.4а) меняем знак аргумента функции
![]() и используем (3.4)
и используем (3.4)
 .
(3.4б)
.
(3.4б)
Дифференцируем (3.4а) и (3.4б)
![]() ,
,
![]() .
(3.5)
.
(3.5)
Функция знака аргумента
От лат. sīgnum – «знак»
 (3.11)
(3.11)

Свойства
Функция нечетная
![]() ,
,
![]() .
(3.12)
.
(3.12)
Выполняется
![]() ,
,
кроме
точки
![]() .
.
Связь с функцией Хевисайда и дельта-функцией
Графически получаем
![]() ,
(3.13)
,
(3.13)
откуда
![]() .
(3.13а)
.
(3.13а)
Графически находим
![]() ,
(3.13б)
,
(3.13б)
тогда с учетом (3.3)
![]() ,
,
![]() ,
,
получаем
![]() .
(3.14)
.
(3.14)
Фурье-образ
Используем (1.1)
 ,
,
где
для сходимости интегралов при
![]() введено
введено
![]() ,
,
![]() .
.
Используем
 ,
,
 ,
,
получаем фурье-образ функции знака
![]() .
(3.19)
.
(3.19)
Из (3.19) и (3.13), (2.35) в виде
![]() ,
,
![]() ,
,
получаем фурье-образ функции Хевисайда
![]() .
(3.20)
.
(3.20)
Используем теорему Фурье о парах функций:
если
![]() ,
,
то
![]() .
.
С учетом (3.19) полагаем
![]() ,
,
![]() ,
,
тогда
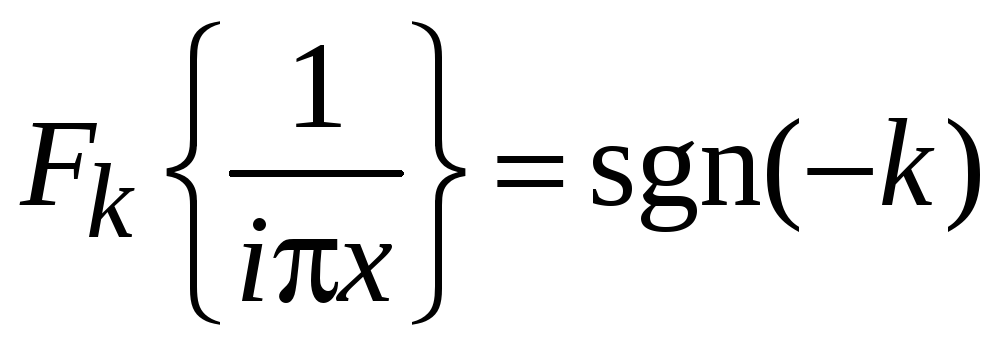 .
.
Используем (3.12) и (3.13а)
![]() ,
,
![]() ,
,
получаем
 .
(3.21)
.
(3.21)
Прямоугольная функция
Прямоугольная
функция
![]() симметричная, имеет единичную ширину
и высоту. Скачок функции на единицу
происходит при
симметричная, имеет единичную ширину
и высоту. Скачок функции на единицу
происходит при
![]() :
:
 (3.27)
(3.27)

Произвольная прямоугольная функция
 .
.
Докажем, что функция симметрична относительно точки c, как показано на рисунке, имеет ширину b и высоту h.

Координату
оси симметрии
![]() находим из условия на аргумент функции
находим из условия на аргумент функции
![]() ,
,
получаем
![]() .
.
Координаты
точек скачка
![]() находим из условий на аргумент функции
находим из условий на аргумент функции
 ,
,
получаем
![]() .
.
Ширина функции
![]() .
.
Свойства
Функция четная
![]() ,
,
имеет значения 0 или 1, тогда
![]() ,
,
![]() ,
,
![]() (3.28)
(3.28)
Связи с другими функциями
Используя графики функций, самостоятельно доказать:
 ,
,
 ,
,
 .
.
Из
 ,
,
![]()
получаем
 .
(3.29)
.
(3.29)
Выполняется
 .
.
Доказательство
Сравниваем
положения точек скачка функций. Для
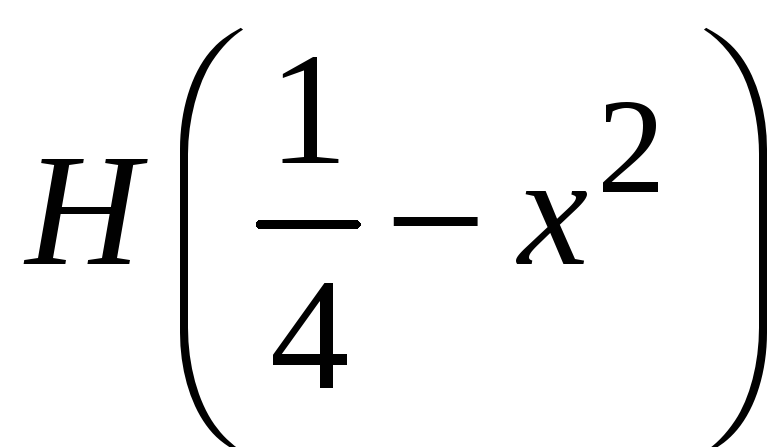 находим
находим
![]() ,
,
![]() .
.
Результат
совпадает со скачками
![]() .
При
.
При
![]() обе функции равны единице. При
обе функции равны единице. При
![]() обе функции
равны нулю.
обе функции
равны нулю.
Фурье-образ
Используем (1.1) и (3.27)
 ,
,
получаем
![]() .
(3.31)
.
(3.31)
Доказать самостоятельно
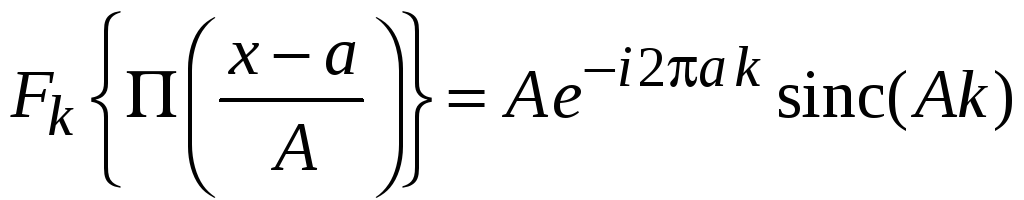 ,
(3.32)
,
(3.32)
 .
(3.33)
.
(3.33)
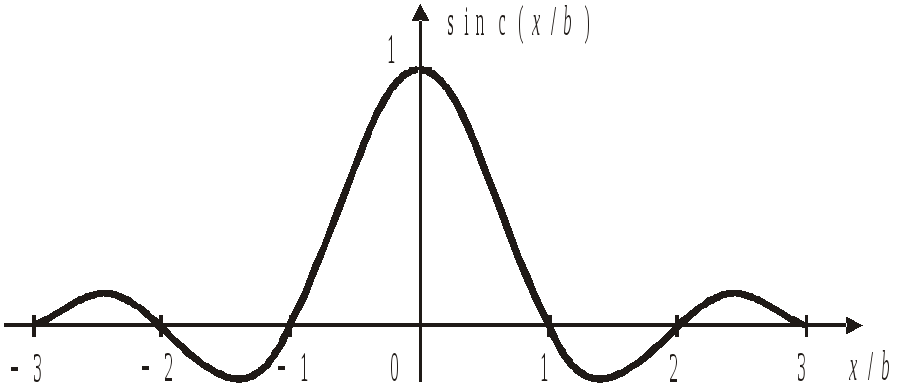
функция sinc
Название от термина «синус»
![]() .
(3.35)
.
(3.35)
Согласно (3.31) является Фурье-образом прямоугольной функции
![]() .
.
Оптическое
преобразование Фурье, осуществляемое
тонкой линзой, как описано на первой
лекции, применяем к функции
![]() .
Она моделирует щель шириной 1, через
которую идет световая волна, как показано
на рисунке. Функция
.
Она моделирует щель шириной 1, через
которую идет световая волна, как показано
на рисунке. Функция
![]() описывает амплитуду дифрагированной
по Фраунгоферу волны на щели единичной
ширины.
описывает амплитуду дифрагированной
по Фраунгоферу волны на щели единичной
ширины.

Амплитуда дифракция на щели
Для
щели шириной
![]() получаем
получаем
![]() ,
(3.35а)
,
(3.35а)
Чем шире щель, тем ближе к началу координат нули ее спектра, и наоборот, в соответствии с теоремой Фурье о частотной полосе.
Функция четная
![]() .
.
Нули функции при
![]()
Выполняется
![]() ,
,
![]()
Из (3.35) с учетом «замечательного предела» получаем
![]() .
(3.36)
.
(3.36)
Числовой расчет дает положения и величины экстремумов
-
|x|
0
1,43
2,46
3,47

1
–0,22
0,13
–0,09
Фурье-образ
Спектр
![]() является прямоугольной функцией, равной
единице в полосе
является прямоугольной функцией, равной
единице в полосе
![]() и нулю вне
этой полосы
и нулю вне
этой полосы
![]() .
(3.41а)
.
(3.41а)
Доказательство
Используем теорему Фурье о парах функций:
если
![]() ,
,
то
![]() .
.
Полагаем
![]() ,
,
используя (3.31)
![]() ,
,
берем
![]() .
.
Учитываем
![]() ,
,
и получаем (3.41а).
Доказать самостоятельно
 .
(3.41б)
.
(3.41б)
При
![]() из (3.41б) следует, что функция
из (3.41б) следует, что функция
![]() имеет
спектр
равный единице в полосе
имеет
спектр
равный единице в полосе
![]() ,
и нулевой
вне этой полосы.
,
и нулевой
вне этой полосы.
Из
(3.41б) при
![]() получаем
получаем
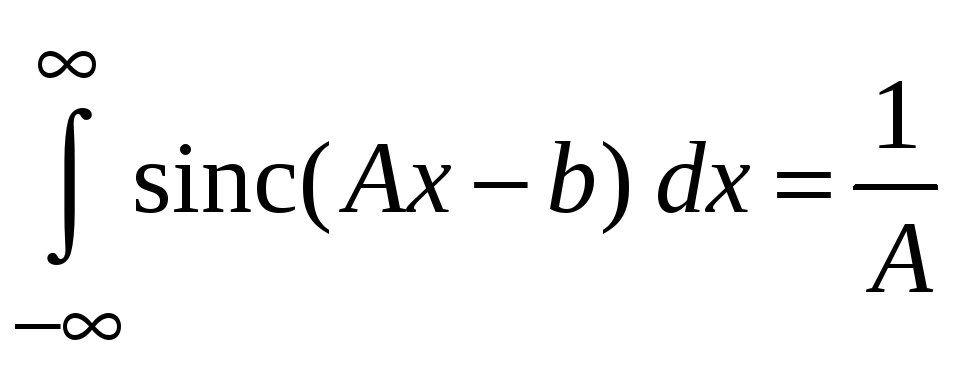 ,
,
 .
(3.38)
.
(3.38)
Площадь
под кривой
![]() равна единице.
равна единице.
Из (3.32)
 ,
,
при
![]() находим
находим
 .
(3.37)
.
(3.37)
Усреднение функции
Среднее
![]() по интервалу Т
около точки x
равно сумме значений функции в указанном
интервале, деленное на ширину интервала:
по интервалу Т
около точки x
равно сумме значений функции в указанном
интервале, деленное на ширину интервала:
 .
(3.42)
.
(3.42)
Выражаем (3.42) через прямоугольную функцию. Используем (3.27)

находим

Получена
прямоугольная функция величиной 1 в
интервале шириной T
с центром в точке a.
Вне этого интервала функция равна нулю.
При
![]() получаем интервал интегрирования в
(3.42), тогда
получаем интервал интегрирования в
(3.42), тогда
 .
.
Последний интеграл является сверткой, тогда
 .
(3.42а)
.
(3.42а)
Усреднение функции по интервалу шириной Т является сверткой функции с прямоугольной функцией шириной Т.
Фурье-образ усредненной функции
При
усреднении функции по интервалу Т ее
Фурье-образ модулируется функцией
![]()
![]() .
(3.42б)
.
(3.42б)
Чем
меньше интервал усреднения, тем сильнее
меняется спектр при удалении от точки
![]() .
.
Доказательство
Используем (3.42а)
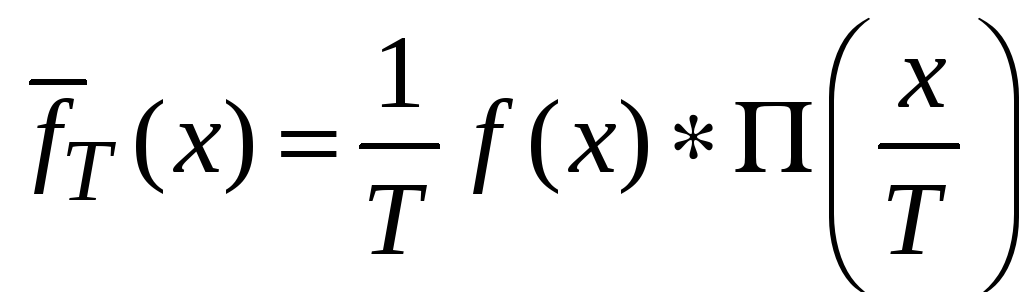 .
.
По теореме Фурье о свертке (1.24)
![]() ,
,
с учетом (3.32)

получаем (3.42б).
Треугольная функция
Обозначается буквой Λ – «лямбда» греческого алфавита
 (3.43)
(3.43)
Площадь под графиком функции равна единице
 .
.

Связь с прямоугольной функцией
1. Свертка прямоугольных функций является треугольной функцией
![]() .
(3.43а)
.
(3.43а)
Доказательство
 ,
,
где
для
![]() использовано
использовано

Последний интеграл по единичному интервалу вокруг точки x вычисляется с помощью рисунка.

Толстая
линия длиной 1 с центром в точке x
показывает интервал интегрирования.
Площадь перекрытия, показанная серым
цветом, равна
 .
При равномерном перемещении интервала
интерирования от
.
При равномерном перемещении интервала
интерирования от
![]() до
до
![]() увеличивается площадь перекрытия
равномерно от 0 до 1 и дает график
увеличивается площадь перекрытия
равномерно от 0 до 1 и дает график
![]() .
.
2. Усреднение прямоугольной функции по единичному интервалу с центром в точке x дает треугольную функцию
 .
(3.43б)
.
(3.43б)
Доказательство
Из определения усреднения (3.42а)
 ,
,
при
![]() ,
,
![]() с учетом (3.43а)
с учетом (3.43а)
![]()
находим
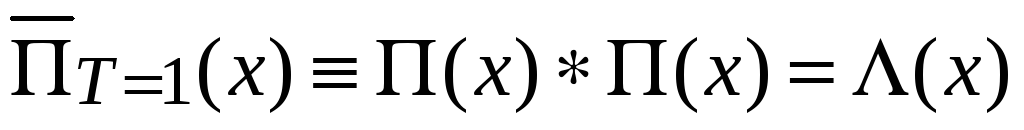 .
.
Фурье-образ
Фурье-образ треугольной функции равен квадрату функции sink
![]() .
(3.43в)
.
(3.43в)
Доказательство
Используем (3.43а) и (3.31)
![]() ,
,
![]() ,
,
и теорему Фурье о свертке (1.24), получаем (3.43а).
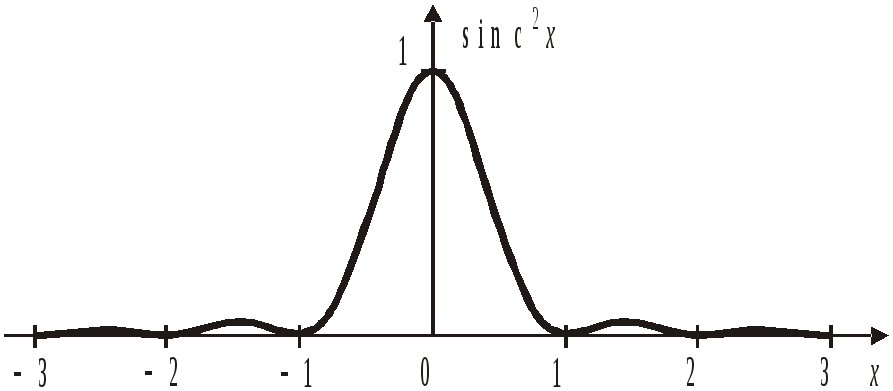
Функция
![]()
Из (3.35) получаем
 .
(3.43г)
.
(3.43г)
Функция четная
![]() .
.
Нули
функций
![]() и
и
![]() совпадают
совпадают
![]()
Численные
расчеты дают положения и значения
максимумов
![]() :
:
-
|x|
0
1,43
2,46
3,47
sinc2x
1
0,05
0,02
0,01
Используя (1.1) и (3.43б), доказать самостоятельно
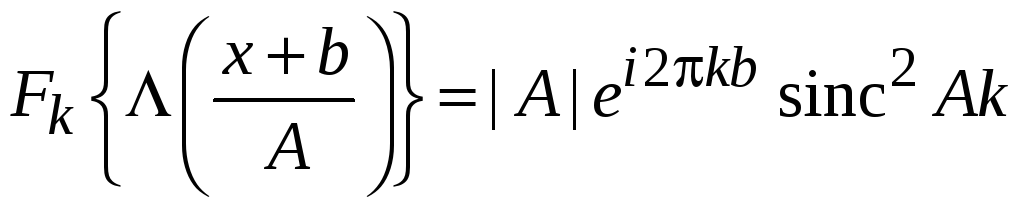 .
(3.44)
.
(3.44)
Выполняется
 ,
(3.45)
,
(3.45)
![]() .
(3.45а)
.
(3.45а)
Фурье-образом
функции
![]() является треугольная функция.
является треугольная функция.
Доказательство
Используем
(3.44) при
![]() ,
и полагаем
,
и полагаем
![]() ,
,
тогда
![]() .
.
По теореме о парах функций Фурье (1.21)
![]() ,
,
получаем (3.45).
При
![]() из (3.45) получаем
из (3.45) получаем
 ,
,
следовательно,
площадь
под графиком функции
![]() равна единице.
равна единице.