Присоединенные функции Лежандра

, ;;

Основные характеристики:

• входят в состав сферических функций, которые описывают угловую зависимость состояния объекта в сферической системе координат ;

• являются собственными функциями оператора момента импульса;

• число n связано с модулем момента импульса;

• число m связано с проекцией момента импульса на ось z. Для проекций возможны положительные и отрицательные значения. Проекция вектора не может быть больше его модуля, поэтому

, .

Уравнение с аргументом X

Присоединенные функции Лежандра удовлетворяют уравнению

(6.115)

При получаем уравнение Лежандра (6.93)

,

следовательно,

.

Уравнение с угловым аргументом

Учитываем

,

заменяем

, ,,

для получаем уравнение

. (6.116)

Форма Родрига

Приводимые далее результаты получены в учебнике путем решения уравнения (6.115) методом факторизации.

1. Первая форма для

(6.117)

Следовательно:

при четном функцияявляется полиномом;

при нечетномсводится к произведениюи полинома;

при выполняется

.

Из (6.117) и (6.96)

,

находим связь с полиномом Лежандра

. (6.118)

2. Вторая форма для

(6.119)

отличается от первой формы (6.117) кратностью дифференцирования.

3. Используем (6.117)

,

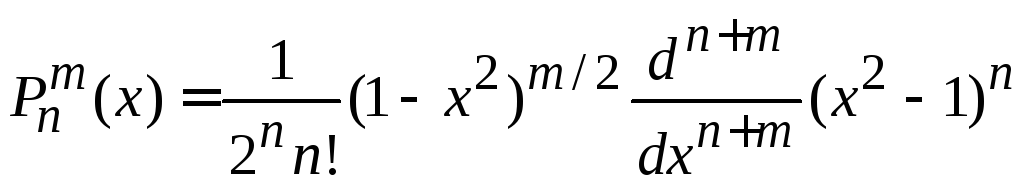заменяем

,

сравниваем с (6.119) и получаем соотношение между функциями с положительным и отрицательным m

, . (6.120)

Низшие порядки

Используем (6.117) и (6.119)

,

.

Находим выражения для функций низших порядков:

;

, , ;

, , ;

, ;

.

Выполняются свойства четности и частные выражения

;

при ,

;

.

Выражение через полином

Используем связь присоединенных (6.118) и обычных полиномов Лежандра (6.98)

,

.

Учитываем

,

получаем полиномиальную форму

. (6.121)

Ортонормированность

Для одинаковых верхних индексов выполняется

. (6.123)

Для одинаковых нижних индексов

. (6.124)

Рекуррентные соотношения

Рекуррентные соотношения для присоединенных полиномов Лежандра получим из рекуррентных соотношений для обычных полиномов Лежандра.

1. Соотношение (6.110)

,

дифференцируем раз

,

умножаем результат на , сравниваем с (6.118)

и получаем

. (6.125)

2. Соотношение (6.104)

,

дифференцируем m раз

.

Для правой стороны применяем формулу Лейбница (6.45)

при допускает толькои, это дает

.

Тогда получаем

.

Результат умножаем на , используем (6.118)

,

находим

. (6.126)

3. Исключаем из (6.126) и (6.125)

.

Получаем соотношение с одинаковыми верхними индексами

. (6.127)

4. Дифференцируем однократно (6.117)

,

находим

.

Умножаем результат на

,

и сравниваем с (6.118)

.

Получаем

. (6.128)

5. Дифференцируем (6.119)

,

находим

,

умножаем результат на и сравниваем с (6.119)

.

Учитывая

,

,

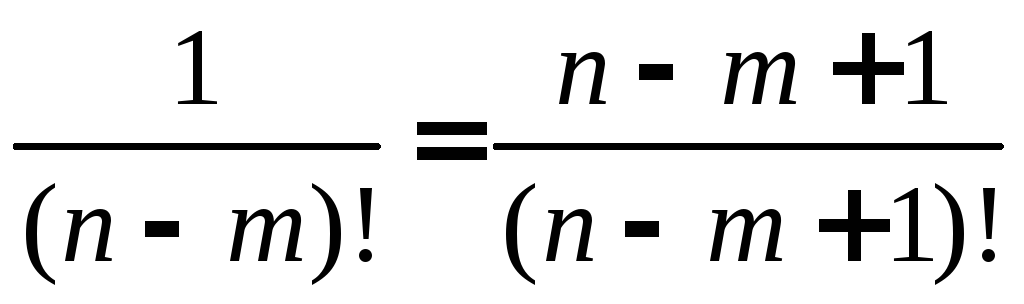получаем

. (6.130)

6. Из (6.130) вычитаем (6.128)

находим

. (6.132)