
ivan
.pdf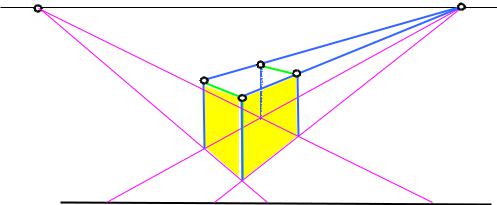
110 |
Глава 2. ЛИНЕЙНАЯ ПЕРСПЕКТИВА |
Описание построения перспективы четырехугольника – нижнего основания параллелепипеда – приведено в разделе 2.4.2 (рис. 57).
После того как построена перспектива нижнего основания призмы, на основании картины О1О от точки О5 откладываем значение высоты призмы и соединяем конец полученного отрезка с точкой схода F1. В пересечении проведенного луча NF1 и перпендикуляров, восстановленных из двух дальних вершин основания, получим точки 5 и 3, которые соединим с точкой схода другого направления прямых, точкой F, пересечение проведенных отрезков с перпендикулярами, восстановленными из двух ближних вершин основания, определит положение точек 4 и 2. Соединив точки 2,4,3 и 5 между собой последовательно, получим верхнее основание призмы. Перпендикуляры, соединяющие вершины верхнего и нижнего основания, являются перспективой ребер призмы (рис. 83).
h1 |
|
h |
|
|
|
F1 |
P |
F |
|
|
O1 |
O2 |
O3 |
O4 |
O5 |
|
||||
|
Рис. 83. |
Перспектива ребер призмы (к рис. 82) |
|
|
Из рис. 82 видно, что для построения масштаба высоты призмы можно использовать любую точку, например О2, О3, или О4 (не обязательно О5).
На рис. 82 и 83 приведен пример построения угловой перспективы правильной призмы, с двумя точками схода. Это наиболее интересный случай построения перспективы предметов подобной формы, например, построение интерьера комнаты (рис. 84).
Параллельная перспектива правильной призмы (см. раздел 1.2, рис. 1) с одной точкой схода менее наглядна, и ее построение можно выполнить, используя способ масштабов (рис. 85).
2.5. Перспектива многогранников и предметов круглой формы |
111 |
|
|
Рис. 84. Перспектива шкафа
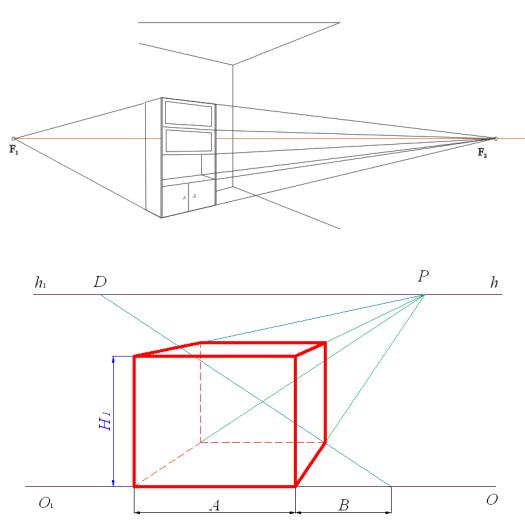
Рис. 85. Перспектива правильной призмы
Построение перспективы начинаем, как всегда, с нанесения на картине ее основных элементов, выбор которых осуществляет сам исполнитель с учетом наглядности изображения: основания картины – линии О1О; линии горизонта – h1h; главной точки картины – Р и дистанционной точки – D. Далее, от произвольной точки на масштабе широт (на основании картины) откладываем отрезок, равный размеру одной из сторон основания призмы, и его концы соединяем с точкой P (как точкой схода параллельных лучей, расположенных перпендикулярно картинной плоскости). Используя масштаб глубин, на осно-
112 |
Глава 2. ЛИНЕЙНАЯ ПЕРСПЕКТИВА |
вании картины откладываем от конца предыдущего отрезка расстояние, равное размеру другой стороны основания призмы и соединяем полученную точку с точкой D (см. раздел 2.4.1, рис. 45). Пересечение проведенных лучей позволит определить одну из дальних вершин нижнего основания призмы, для получения второй вершины проведем через полученную вершину прямую, параллельную основанию картины. Высота призмы определяется по масштабу высот: отложим от концов первого отрезка расстояние, равное высоте призмы, концы полученных отрезков соединим с точкой P и достроим верхнее основание призмы и дальнюю грань.
Построение перспективы пирамиды также начинаем с построения ее основания: для усеченной пирамиды – с перспективы нижнего основания (рис. 86). По условию задачи пирамида – правильная, а в основании лежит квадрат.
D
S
H
P
|
|
|
3 |
|
4 |
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
О1 |
|
|
|
|
|
|
|
|
|
|
|
О |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
О2 |
О3 |
О4 |
О5 |
О6 |
|
|
|
|
L |
|
B |
|
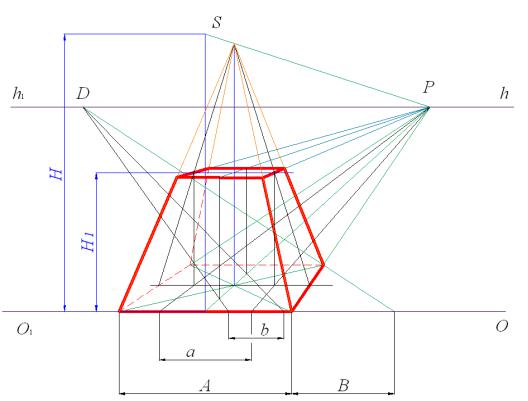
Рис. 86. Перспектива пирамиды полной и усеченной
2.5. Перспектива многогранников и предметов круглой формы |
113 |
|
|
Для выполнения перспективы пирамиды используем метод масштабов: для построения основания – масштабы широт и глубин, для построения вершины (или высоты для усеченной пирамиды) масштаб высот. Используя масштаб широт, на основании картины в любом месте на чертеже откладываем значение стороны квадрата L. Начало и конец отрезка L соединяем с главной точкой картины P как точкой схода параллельных лучей, расположенных перпендикулярно картинной плоскости.
Используя масштаб глубин, от конца отрезка L вправо откладываем отрезок B, равный расстоянию, на котором пирамида находится вглубь относительно картины. Соединив конец отрезка B (точку О6) с точкой D, получим две вершины в основании пирамиды: точку 1 при пересечении с прямой О5P и точку 3 – при пересечении с отрезком О2P. Далее находим вершину 2, как точку пересечения отрезка 1-2, параллельного основанию картины, и отрезка О2P, аналогично определяем положение последней вершины основания (точку 4): из точки 3 проводим отрезок, параллельный основанию картины. Для построения вершины пирамиды выполним следующее: с помощью диагоналей определяем в основании пирамиды центр, затем восстанавливаем из полученной точки перпендикуляр. Величину высоты пирамиды (отрезок H) откладываем на основании картины от точки О4 , конец отрезка H соединяем с точкой P. Точка пересечения проведенного отрезка и перпендикуляра, восстановленного из центра основания, определит положение вершины пирамиды. Теперь закончим построение, соединив основание пирамиды с вершиной.
Построение перспективы верхнего основания пирамиды (в том случае, когда дана усеченная пирамида) выполняется аналогично: с помощью масштаба высот на отрезке H отмеряем нужную высоту и соединяем конец полученного отрезка с главной точкой картины (Р), получим центр верхнего основания. Центр верхнего основания соединяем с точкой D, так как она является точкой схода для прямых, расположенных под углом 45° к картинной плоскости. Диагонали оснований пирамиды (квадратов) и есть такие прямые. Отрезок, соединяющий дистанционную точку и центр, позволит определить положение двух вершин квадрата: одну при пересечении ребра 1-S, другую – при пересечении ребра 3-S. Остальные две вершины строим из полученных точек как перспективу прямых, параллельных картине до пересечения с ребрами 2-S и 4-S.
Задание. Построить перспективу усеченной пирамиды, основаниями которой являются прямоугольники: размеры нижнего основания 80×50 (мм), высота неусеченной пирамиды 100 мм, верхнее основание находится на расстоянии 70 мм от нижнего. Определить размеры верхнего основания. Проверьте свое решение по рис. 86 (а и в – стороны верхнего основания).
114 |
Глава 2. ЛИНЕЙНАЯ ПЕРСПЕКТИВА |
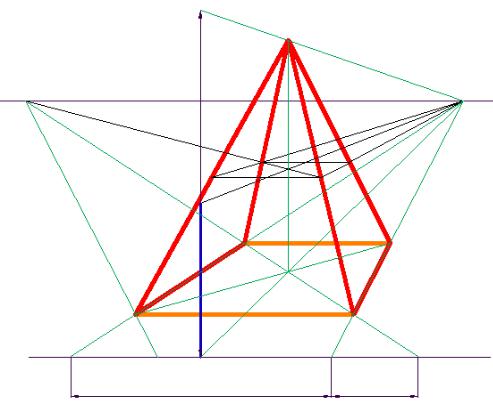
Для выполнения перспективы усеченной пирамиды, основаниями которой являются прямоугольники (в предыдущем примере были квадр а- ты), потребуются дополнительные построения (рис. 87), так как точка D не является точкой схода для диагоналей оснований пирамиды (прямоугольников).
Рис. 87. Построение перспективы усеченной пирамиды и определение размеров верхнего основания
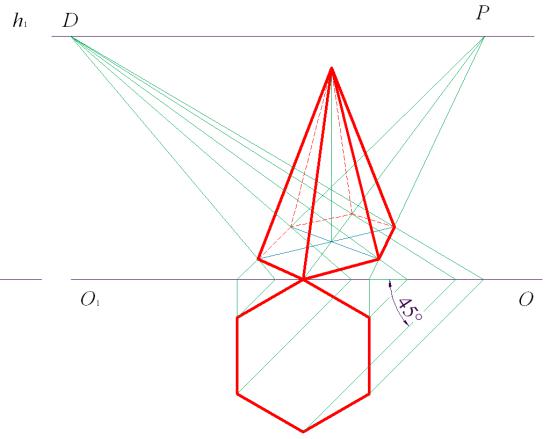
Для построения перспективы правильной пирамиды, в основании которой лежит многоугольник (например, шестиугольник, рис. 88), воспользуемся способом совмещения плоскостей. В данном примере шестиугольник расположен таким образом, что две его стороны перпендикулярны картинной плоскости, следовательно, для них точкой схода является главная точка картины, точка P. Перспективу вершин многоугольника определим как точки пересечения прямых, направленных в точки схода P и D от основания картины. Точ-
2.5. Перспектива многогранников и предметов круглой формы |
115 |
|
|
ка D – дистанционная точка, она же является точкой схода для прямых, составляющих угол 45° с картинной плоскостью (см. раздел 2.4.1, рис. 45), поэтому каждую из вершин четырехугольника проецируем на основание картины под углом 45°.
Рис. 88. Перспектива правильной пирамиды
Если все стороны многоугольника расположены по отношению к картинной плоскости под углом, отличным от 90°, то для построения перспективы пирамиды нужно воспользоваться масштабными точками (см. раздел 2.4.2,
рис. 58).
Для построения призмы, в основании которой лежит многоугольник, можно воспользоваться и другими способами. Например, в разделе 2.4.3 пяти-
116 |
Глава 2. ЛИНЕЙНАЯ ПЕРСПЕКТИВА |
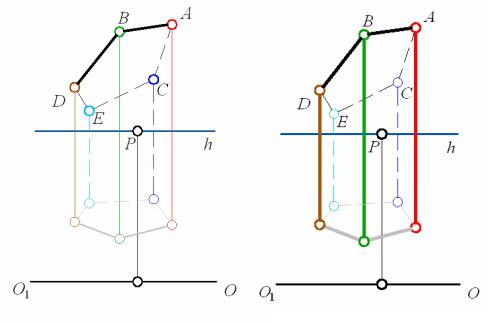
угольник построен радиальным способом (рис. 89, а). Если линии связи, соединяющие перспективу и вторичную проекцию многоугольника, «превратим» в ребра, то получится призма (рис. 89, б).
а |
б |
Рис. 89. Перспектива: а – пятиугольника; б – призмы
Задание. Построить перспективу призмы, основаниями которой являются пятиугольники, используя масштабные точки и масштаб высот: размеры и положение по отношению к картинной плоскости взять произвольно.
Построение предметов круглой формы, в основании которых лежит окружность, сводится к построению перспективы основания всеми известными способами, чаще всего используются способы описанного квадрата или его половины, или его четверти. Подробное описание такого способа приведено в разделе 2.4.2, кроме этого можно использовать и другие способы, например, радиальный архитектора. Но эти способы применяют при построении перспективы сложных предметов, в которых есть отверстия или выступы круглой формы. Рассмотрим построение перспективы для данной категории предметов на примере перспективы цилиндра (рис. 90) и конуса (рис. 91).
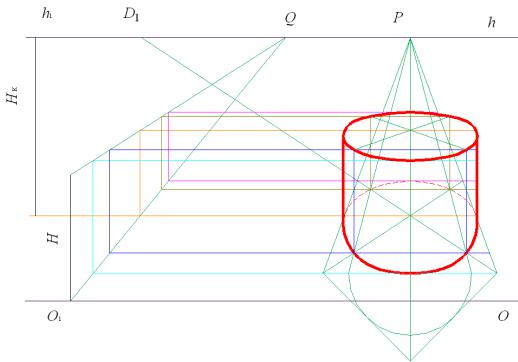
Перспективу цилиндра, стоящего на предметной плоскости, начинаем выполнять с его нижнего основания (рис. 90). Для этого используем половину квадрата, описанного вокруг окружности. Этот способ позволяет определить
2.5. Перспектива многогранников и предметов круглой формы |
117 |
|
|
Рис. 90. Перспектива цилиндра
8 точек, принадлежащих перспективе нижнего основания цилиндра, соединив которые и получим необходимое изображение. Для построения верхнего основания используем масштаб высот: из каждой полученной точки проводим перпендикуляры, а со шкалы масштаба высот – горизонтальные прямые, пересечение прямых образует восемь точек. Плавное соединение полученных точек даст перспективу верхнего основания цилиндра. В данном случае мы упростили построение перспективы цилиндра, так как не применили способ квадрата для верхнего основания, а воспользовались масштабом высот.
Шкала масштаба высот построена в любом месте чертежа от произвольной точки (точки Q). В примере ось вращения цилиндрической поверхности находится на одной прямой с главной точкой картины. Такое положение не всегда бывает наглядным. Для выполнения перспективы цилиндра, расположенного справа от точки P, воспользуйтесь рис. 66, приведенным в разделе 2.4.2.
Задание. Построить перспективу прямого кругового цилиндра, стоящего на предметной плоскости, на расстоянии 20 мм от картины, диаметр основания которого равен 50 мм, высота 90 мм, а ось вращения расположена правее точки P.
118 |
Глава 2. ЛИНЕЙНАЯ ПЕРСПЕКТИВА |
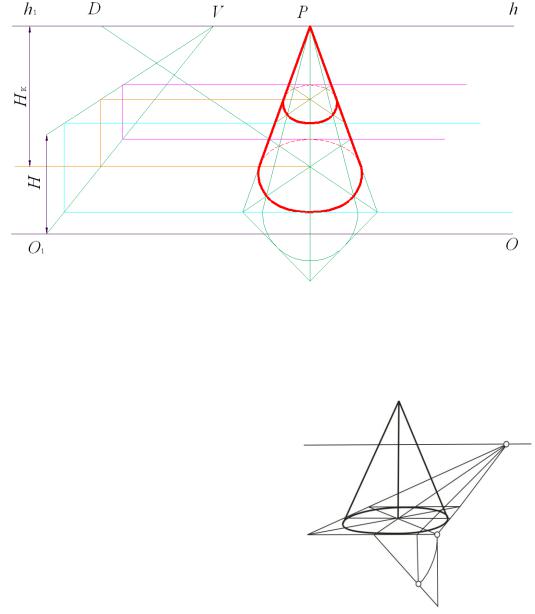
Перспектива основания прямого кругового конуса (рис. 91) выполнена аналогично построению перспективы цилиндра (рис. 90), положение вершины конуса определено с помощью масштаба высот.
Рис. 91. Перспектива конусов: полного и усеченного
На этом же рисунке (рис. 91) построена перспектива усеченного конуса. Для построения верхнего основания применен также масштаб высот, но при построении необходимых восьми точек эллипса использовались не перпендикуля-
ры (как при построении цилиндра), а об- |
|
|
разующие поверхности конуса, проведен- |
|
|
ные из четырех точек нижнего основания. |
P |
|
В примере, приведенном на рис. 91, ось |
|
|
вращения находится на одной прямой с |
|
|
точкой P, поэтому образующие, прове- |
|
|
денные из четырех искомых точек, совпа- |
|
|
дают с линиями схода, проведенными к |
|
|
главной точке картины. |
|
|
Задание. Построить перспективу |
|
|
усеченного прямого кругового конуса, |
|
|
стоящего на предметной плоскости, ось |
|
|
вращения |
которого расположена левее |
|
точки P. |
Диаметр основания равен 60 мм, |
Рис. 92. Перспектива конуса |
2.5. Перспектива многогранников и предметов круглой формы |
119 |
|
|
высота – 80 мм, а расстояние конуса до картины – 35 мм. При выполнении задания воспользуйтесь рис. 67, 90.
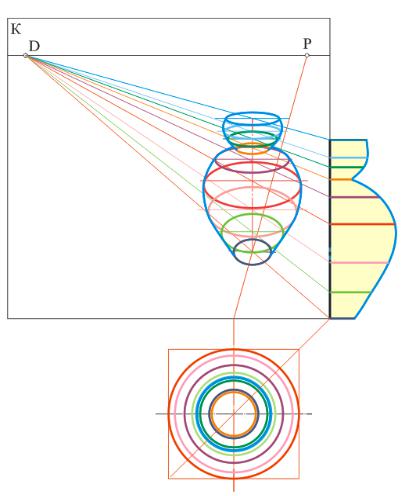
С помощью описанных квадратов можно построить окружности, которые будут служить каркасом поверхности вращения (рис. 93). В этом случае нужно выполнить окружности, расположенные в плоскостях, перпендикулярных оси вращения, и параллельные между собой. Количество окружностей определяет точность построения поверхности: чем их больше, тем больше будет параллелей, описывающих каркас поверхности вращения, а значит, и точность будет выше. Каркас, состоящий из окружностей, позволяет построить перспективу очерка заданной поверхности.
Рис. 93. Перспектива поверхности
