metodichka_2_semestr

Министерство образования и науки Российской Федерации НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ЧИСЛЕННЫЕ МЕТОДЫ

И

ПРОГРАММИРОВАНИЕ НА «ФОРТРАНЕ»

Методические указания для проведения лабораторных работ

для студентов 1,2 курсов факультета летательных аппаратов

НОВОСИБИРСК

2

2010

ББК 73я7

И741

Составители: канд. техн. наук Н.В. Третьякова, канд. физ.-мат. наук П.Е. Рябчиков

Рецензент: канд. физ.-мат. наук А.А. Поздеев

Работа выполнена на кафедре Самолето- и вертолетостроения

* Новосибирский государственный технический университет, 2010

2

СОДЕРЖАНИЕ

Лабораторная работа №1. Приближенные методы решений нелинейных уравнений…………………………………………………………………………….4

Лабораторная работа №2. Численное интегрирование …..……………………….4

Лабораторная работа №3. Определение длины кривой…..……………………….4

Лабораторная работа №4. Решение систем линейных уравнений методом Гаусса ….……………………………………………………………………..……….4

Лабораторная работа №5. Решение систем линейных алгебраических уравнений методом простых итераций ….…………………………………………………...….4

Лабораторная работа №6. Решение задачи Коши ….…………………...………….4

2

Лабораторная работа №1 Приближенные методы решений нелинейных уравнений

Нахождение корней уравнения – это одна из древнейших математических

которые мы будем рассматривать, не имеют аналитических формул для своих корней. Поэтому приходиться пользоваться приближенными методами нахождения корней, которые в основном состоят из двух этапов:

1)отыскание приближенного значения корня;

2)уточнение приближенного значения корня до некоторой заданной степени точности.

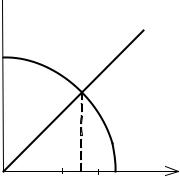
Часто приближенное значение корня бывает известно из физических соображений, в других случаях можно использовать графические методы. Так

если требуется локализовать корень уравнения cos(x) x 0 , то переписав это

y

Y2 cos(x)

Y1 x

2

Рис.1

Абсцисса x точки пересечения функций Y1 и Y2 будет искомым корнем. В

данном случае корень лежит внутри отрезка [0,7;0,8]. Если же не удается локализовать корень графически, то его можно найти с помощью грубого анализа функции. В основном этот анализ сводиться к тому, что отыскиваются

ервого положительного корня нелинейного уравнения можно воспользоваться следующим алгоритмом.

Алгоритм метода локализации корня

1. Зададим начальное значение x , конечное значение xk , шаг h , c которым

предполагаем менять значения аргумента функции F x . Если уравнение не имеет нулевого корня, то можно положить x 0 .

2.Вычислим значение функции для начального значения x : Y F x .

3.Изменим значение x на величину шага h : x x h .

4.Вычислим значение функции для нового значения x : Z F x .

5.Проверим условие x xk (текущее значение x не превысило заданный конец

интервала). Если x xk , то в данном интервале x, xk корня нет и необходимо

идти на пункт 1, т.е., вводить новые начальные значения. Если x xk , проверяем

2

6. Если функция сменила знак, т.е. Y * Z 0 , то в качестве правой границы B

отрезка локализации корня выбирается текущее значение аргумента x , а в качестве левой границы A – предыдущее значение x : a x h, b x .

После того, как решена первая задача – отыскание приближенного значения корня, можно перейти ко второй – уточнению корня до некоторой заданной степени точности. Существуют различные методы уточнения корней.

Одним из методов уточнения корней является метод половинного деления.

Метод половинного деления

Метод половинного деления состоит в построении последовательности

вложенных отрезков, на концах которых функция принимает значения

разных знаков. Каждый последующий отрезок получают делением предыдущего пополам. Процесс построения последовательности отрезков позволяет найти

корень функции F x с любой заданной точностью.

Алгоритм метода половинного деления

1. Задаются начальные значения левой a и правой b границ локализации корня и точность вычисления корня .

2. Вычисляется значение функции F x в точке a : Y F a .

3. Определяется середина отрезка a,b : c 0.5*(a b) .

4. Вычисляется значение функции F x в точке с : Z F c .

5. В зависимости от того, в какой половине старого отрезка a,с или с,b

лежит корень, выбирается граница – левая или правая – нового отрезка a,b :

2

если Y * Z 0 , то a c иначе: b c . Новый отрезок a,b в два раза меньше предыдущего.

6. Выполняется проверка на достижение заданной точности, если b a –

идти на пункт 3.

7. Если же точность вычислений достигнута, результат выводится на печать.

Графически данный метод можно пояснить на следующем примере:

y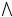

f ( x)

Y f (a)

Рис.2

Метод половинного деления – наиболее универсальный метод отыскания корней нелинейных уравнений. К его недостаткам относится невысокая скорость сходимости. Для достижения точности необходимо совершить n итераций,

где

n log2 b a / .

2

Итерационные методы

Численный метод, в котором производится последовательное, шаг за шагом, уточнение первоначального грубого приближения, называется методом итераций. Каждый шаг в таком методе называется итерацией. Если при последовательных итерациях получаются значения, которые все ближе и ближе приближаются к истинному значению корня, то говорят, что метод итераций сходится.

2

Метод последовательных приближений

Предположим, что уравнение F x 0 переписано в виде

Например, для F x cos(x) x 0 ; x cos(x) , т. е. (x) cos(x) .

Пусть x0 будет исходным приближенным значением корня уравнения (2). Тогда

в качестве первого приближения возьмем x1 (x0 ) . В качестве второго

приближения возьмем x2 (x1 ).

Продолжая этот процесс дальше, в качестве n - го приближения необходимо положить

Основной вопрос, который необходимо выяснить при использовании этого метода – сходится ли xn к решению уравнения (2) при возрастании n ?

Выведем достаточные условия для сходимости метода. Эти условия не являются необходимыми, так как существуют функции, для которых эти условия не выполняются, но для которых, тем не менее, с помощью (3) можно найти их решения.

Рассмотрим геометрическое представление процесса: при решении уравнения

(2) отыскивается точка пересечения кривой y (x) и прямой y x .

Рассмотрим рисунок, на котором изображена некоторая кривая y (x) . Эта кривая, может представлять собой какую угодно функцию, но в данном случае

производная этой кривой положительна и меньше единицы, т. е. .

Пусть x a – значение x в точке пересечения, тогда, a является корнем этого

2