Тер.Вер методичка

Формула Байеса

Представим себе следующую ситуацию. До опыта о его исходах можно было сделать ряд гипотез H1, H2, …, Hn. Вероятность гипотез до опыта известна (априорные вероятности). Теперь предположим, что опыт произведен, и в его результате появилось событие A. Нужно пересмотреть вероятности гипотез с учетом этого факта. Другими словами, найти априорные вероятности гипотез при условии, что опыт дал результат A. Ответ на этот вопрос дает формула Байеса:

Пример 4. На фабрике машины № 1, 2 и 3 производят соответственно 25, 35 и 40 % всех изделий. В их продукции брак составляет в среднем 5, 4 и 2 % соответственно. Выбранное наугад изделие оказалось дефектным. Найти вероятность того, что оно было произведено машиной № 1.

Решение. Если задача решается с помощью формулы Байеса, то сначала записывается событие, которое уже произошло, A = {выбранное изделие дефектное}. Затем вводятся гипотезы, причем так, чтобы одна из них была интересующим нас событием. Нас интересует событие H1 = {изделие было произведено машиной № 1} (при условии, что произошло событие A). Теперь необходимо дополнить гипотезу H1 другими гипотезами так, чтобы они образовывали полную группу несовместных событий: H2 = {изделие было произведено машиной № 2} и H3 = {изделие было произведено машиной № 3}.

P(H1) = 0,25; P(H2) = 0,35; P(H3) = 0,4;

P(A|H1) = 0,05; P(A|H2) = 0,04; P(A|H3) = 0,02.

Тогда

Пример 5. Два стрелка независимо друг от друга стреляют по одной мишени. Вероятность попадания первого p1 = 0,8, второго p2 = 0,4. После стрельбы в мишени обнаружена одна пробоина. Найти вероятность того, что в мишень попал первый стрелок.

Решение. A = {в мишени ровно одна пробоина}

H1 = {первый стрелок попал в мишень}; H2 = {первый стрелок промахнулся}.

P(H1) = p1 = 0,8; P(H2) = 1–p1 = 0,2.

Найдем вероятность события A при наступлении гипотезы H1: P(A|H1). Если мы точно знаем, что первый стрелок попал в мишень, то в ней будет одна пробоина, только когда второй стрелок промахнулся, т. е. P(A|H1) = 1–p2 = 0,6. Аналогично P(A|H2) = p2 = 0,4. Тогда

k 1

ЗАДАЧИ К РАЗДЕЛУ VI

1. В первой урне лежало 10 белых и 20 черных шаров, во второй – 10 белых и 10 черных шаров. Из первой урны наугад извлекают 4 шара, из второй – 6 шаров и перекладывают их в третью урну. Какова вероятность того, что шар, извлеченный наугад из третьей урны, окажется белым?

2. В городе три шоколадные фабрики. Первая выпускает 45 % конфет, причем 15 % из них в обертке. Вторая выпускает 35 % конфет, из которых 23 % в обертке. Третья выпускает 20 % конфет, из них 48 % в обертке. Какова вероятность, что купленная наугад конфета окажется без обертки?

3. На столе четыре пакета. В первом 4 шоколадные конфеты и 10 леденцов, во втором 11 шоколадных конфет и 2 леденца, в третьем 20 леденцов, а в четвертом 13 шоколадных конфет. Наугад выбирают один пакет и в нем конфету. Определить:

а) какова вероятность того, что выберут шоколадную конфету; б) какова вероятность выбора конфеты из первого пакета, если она

оказалась шоколадной?

42

4. В магазин поступает минеральная вода в бутылках от двух изготовителей: местного и иногороднего, причем местный изготовитель поставляет 40 % всей продукции. Вероятность того, что при транспортировке бутылка окажется разбитой, равна: для местной продукции 0,02, для иногородней 0,05. Найти вероятность того, что взятая наудачу бутылка окажется неразбитой.

5. Имеется пять урн. В первой, второй и третьей урнах находится по 2 белых и 3 черных шара; в четвертой и пятой урнах по 1 белому и 1 черному шару. Случайно выбирается урна и из нее извлекается шар. Какова вероятность того, что выбрана четвертая или пятая урна, если извлеченный шар оказался белым?

6. Есть 10 симметричных монет: 8 нормальных, а на двух герб находится с обеих сторон. Наудачу взятая монета бросается три раза. Найти вероятность того, что выпадут три герба.

7. На сборку поступают детали с трех автоматов. Первый дает в среднем 0,2 % брака, второй 0,1 % брака; продукция, поступающая с третьего автомата, не содержит бракованных изделий. На сборку поступило 2000 деталей с первого автомата, 3000 деталей со второго автомата и 5000 деталей с третьего автомата:

1)найдите вероятность того, что деталь, выбранная наугад из всех этих деталей, будет бракованная;

2)какова вероятность того, что деталь, выбранная наугад из данных деталей, поступила с первого автомата, если известно, что она яв-

ляется небракованной?

8. Из урны, в которой было m 3 белых и n черных шаров, потеряли один шар неизвестного цвета. Для того чтобы определить состав шаров в урне, из нее наудачу вынуты два шара. Найти вероятность того, что был утерян белый шар, если известно, что вынутые шары оказались белыми.

9. Вероятности попадания в мишень для трех стрелков равны 4/5, 3/4 и 2/3 соответственно. В результате одновременного выстрела трех стрелков в мишени образовалось две пробоины. Какова вероятность того, что 3-й стрелок попал в мишень?

10. В первой урне 4 белых и 6 черных шаров, во второй – 8 белых и 2 черных шара. Из каждой урны наугад удаляют по k шаров (1 k 9), а оставшиеся шары ссыпают в третью, пустую урну. Какова вероятность того, что шар, извлеченный из третьей урны, будет белым?

43

11. Группа студентов состоит из a отличников, b – хорошо успевающих и c занимающихся слабо. Отличники на предстоящем экзамене могут получить только отличные оценки. Хорошо успевающие студенты могут получить с равной вероятностью хорошие и отличные оценки. Слабо занимающиеся могут получить с равной вероятностью хорошие, удовлетворительные и неудовлетворительные оценки. Для сдачи экзамена наугад вызывается один студент. Найти вероятность того, что он получит хорошую или удовлетворительную оценку.

12. В магазине продается 60 % тортов фирмы «Дюжина», 30 % – фирмы «Эстье» и 10 % – фирмы «Инмарко». Вероятность того, что торт фирмы «Дюжина» окажется несвежим, равна 0,2; для тортов, изготовленных фирмами «Эстье» и «Инмарко», эти вероятности соответственно равны 0,1 и 0,3. Найти вероятность того, что купленный в этом магазине торт окажется свежим.

13. Вероятности попадания в мишень для трех стрелков равны 4/5, 3/4 и 2/3 соответственно. Для поражения цели в нее нужно попасть не менее двух раз. В результате одновременного выстрела трех стрелков цель была поражена. Какова вероятность того, что 3-й стрелок попал в цель?

14. В баре разливают 50 % пива «Балтика», 30 % пива «Золотая бочка» и 20 % пива «Очаков». Вероятность того, что пиво «Балтика» окажется «неправильным», равна 0,3; для пива «Золотая бочка» и пива «Очаков» эти вероятности соответственно равны 0,1 и 0,2. Посетитель купил «правильное» пиво. Какова вероятность того, что ему налили пиво «Очаков»?

15.Бросается две игральные кости. Какова вероятность того, что на первой кости выпала единица, если известно, что на второй кости выпало очков больше, чем на первой?

16.В ящике находится a новых теннисных мячей и b игранных. Из ящика наугад вынимается два мяча, которыми играют. После этого мя-

чи возвращаются в ящик. Через некоторое время из ящика снова берут наугад два мяча. Найти вероятность того, что они будут новыми (a 2; b 2).

17. В первом блюде два пирожка с малиной и 4 с лимоном, во втором – 5 пирожков с малиной и 5 с лимоном. Из первого блюда наудачу переложили во второе два пирожка. Найти вероятность того, что потом взятый наудачу из второго блюда пирожок окажется с лимоном.

44

18. Приборы одного наименования изготавливаются двумя заводами; первый завод поставляет 2/3 всех изделий, поступающих на производство; второй 1/3. Надежность (вероятность безотказной работы) прибора, изготовленного первым заводом, равна p1, второго p2. Определить надежность наудачу выбранного прибора.

19.В двух ящиках находятся микросхемы. В первом ящике – 12 микросхем, из них одна нестандартная, во втором – 10 микросхем, из них две нестандартные. Из первого ящика наугад взята микросхема

ипереложена во второй. Найти вероятность того, что наугад извлеченная из второго ящика микросхема будет нестандартной.

20.Перед Новым годом четыре ребенка написали письмо Деду

морозу. Вероятности исполнения их желаний равны 0,95; 0,7; 0,53 и 0,03. Найти вероятность исполнения одного из наудачу прочитанных писем.

21. Вероятность того, что 1-я группа из пяти студентов помнит письмо Онегина Татьяне, равна 0,85; для 2-й группы из 10 студентов эта вероятность составляет 0,5; для 3-й группы из 24 – 0,2. Наудачу выбранный студент получил за этот отрывок «отлично». Найти вероятность того, что отвечал студент из 2-й группы.

22. На компот Нина купила 24 абрикоса и 23 сливы. Дома девушка не удержалась и съела 1 фрукт, причем, неизвестно какой. После этого наудачу она извлекла из сумки еще два фрукта для младшего брата, которые оказались абрикосами. Найти вероятность того, что первоначально были съедены:

а) абрикос; б) слива.

23. В магазине 5 электрических и 6 механических соковыжималок. Вероятность неисправности 0,2 для электрической и 0,1 для механической. Продавец для собственных нужд взяла одну, не обратив внимания, какую. Найдите:

а) вероятность того, что прибор исправен; б) вероятность того, что соковыжималка оказалась электрической,

если известно, что прибор исправен.

24. Магазин приобретает чай у двух фабрик, при этом первая из них поставляет 2/3 всего товара. Продукция высшего сорта для первой фабрики составляет 90 %, а для второй 80 %. Найти вероятность, что купленная наугад пачка чая будет пачкой высшего сорта.

45

25. В двух цехах изготовляется однотипная продукция. Производительность первого цеха вдвое выше, чем производительность второго цеха. Изделия высшего качества составляют в среднем для первого цеха 95 %, для второго – 90 %. Из общей продукции этих цехов наугад берется одно изделие.

а) найти вероятность того, что оно окажется изделием высшего качества.

б) какова вероятность того, что выбранное изделие изготовлено во втором цехе, если известно, что оно оказалось изделием высшего качества?

Р а з д е л VII

СХЕМА БЕРНУЛЛИ

Формула Бернулли

Пусть производится n независимых испытаний, в каждом из которых может появиться или не появиться событие A. Появление события A в каждом испытании называют «успехом», непоявление – «неудачей». Вероятность того, что событие A в серии из n испытаний произойдет ровно k раз и не произойдет n– k раз определяется по формуле Бернул-

ли:

Pn k Cnk pk qn k ,

где q = 1–p вероятность неудачи, т. е. события A . Саму серию испытаний называют схемой Бернулли.

Пример 1. 10 раз подкидывается монета. Найти вероятность того, что ровно два раза выпадет герб.

Решение. Испытание – подкидывание монеты. Очевидно, испытания независимые. Всего испытаний n = 10. Успех A = {выпал герб}.

P A p 1/ 2 , q 1 p 1/ 2 . Число успехов k = 2. Тогда вероятность того, что ровно два раза выпадет герб, равна:

46

Замечание. Прежде чем использовать формулу Бернулли, необходимо убедиться, что испытания независимы.

Пример 2: Известно, что изделия в среднем содержат 5 % брака. Найти вероятность того, что среди пяти наугад взятых изделий: а) нет ни одного бракованного; б) будет ровно два бракованных.

Замечание. Выражение «в среднем 5 %» не означает, что из 100 деталей ровно 5 бракованных, а значит, что вероятность взять бракованную деталь равна 0,05 вне зависимости от того, какая деталь была выбрана для этого.

Решение. За испытание возьмем выбор изделия. Всего испытаний n = 5. Успех A = {изделие бракованное}. p 0,05 , q 1 p 0,95 .

В силу последнего замечания испытания независимы и задача является вероятностной схемой Бернулли.

5 4 0,052 0,953 0,021. 2

Пример 3. Всхожесть семян определенного сорта оценивают с вероятностью p = 0,8. Какова вероятность, что из пяти посеянных семян взойдут не менее четырех?

Решение. Нас интересует вероятность события B = {взойдет не менее 4 семян}. Пусть испытание – наблюдение за одним из посеянных семян (n = 5), а успех A = {семя взойдет}. Воспользоваться напрямую формулой Бернулли нельзя, так как нужно задать конкретное число успехов. Однако эту задачу можно привести к схеме Бернулли:

B = B1 + B2,

B1 = {взойдет ровно 4 семени}; B2 = {взойдет ровно 5 семян}.

47

Последние два события несовместны, поэтому вероятность их суммы равна сумме вероятностей. Оба события являются вероятностной схемой Бернулли:

P(B) = P(B1) + P(B2) = 0,4096 + 0,32768 = 0,73728.

Пример 4. Вероятность рождения мальчика 0,515. В семье 6 детей. Какова вероятность того, что среди них не более двух девочек?

Решение. Испытание – определение пола ребенка. Успех A = {ребенок – девочка}.

B = {из 6 детей не более двух девочек}. Рассмотрим события:

B0 = {в семье нет девочек}; B1 = {в семье одна девочка}; B2 = {в семье две девочки}.

B = B0 + B1 + B2

n = 6; p = 0,485; q = 0,515.

6 5 0, 4852 0,5154 0, 248201; 2

P(B) = P(B0) + P(B1) + P(B2) = 0,37228.

48

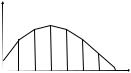
Наивероятнейшее число наступлений события

Вероятности Pn(k) при данном n сначала увеличиваются при увеличении k от 0 до некоторого значения k0, а затем уменьшаются при изменении k от k0 до n. Поэтому k0 называют

наступления события A в n испытаниях.

k0 = np. Если np–q и np + p целые числа, то наивероятнейших чисел наступления события будет два: k0(1) np q и k0(2) np p , и их ве-

роятности будут равны Pn k0(1) Pn k0(2) .

Пример 5. Батарея дала 14 выстрелов по объекту. Вероятность попадания в объект p = 0,2. Найти наивероятнейшее число попаданий и вероятность этого числа попаданий.

Решение. p = 0,2 – вероятность попадания в объект; q = 0,8 – вероятность промаха; n = 14. Наивероятнейшее число попаданий k0 определяется из неравенств np – q ≤ k0 ≤ np + p:

np = 14 0,2 = 2,8; 2,8 – 0,8≤k0 ≤ 2,8 + 0,2; 2 ≤ k0 ≤ 3.

Таким образом, наивероятнейшее число попаданий равно 2 и 3. Найдем их вероятности:

Пример 6. Вероятность попадания в цель при каждом выстреле равна p = 0,8. Сколько нужно произвести выстрелов, чтобы наивероятнейшее число попаданий было равно 20?

49

Решение. p = 0,8 – вероятность попадания; q = 0,2 – вероятность промаха; k0 = 20 – наивероятнейшее число попаданий; число выстрелов n – ?. Для определения n воспользуемся неравенствами np – q ≤ k0 ≤ np + p:

n 0,8 – 0,2 ≤ 20 ≤ n 0,8 + 0,8 19,2 ≤ n 0,8 ≤ 20,2 24 ≤ n ≤ 25,25.

Так как n – целое число, то оно может быть равно либо 24, либо 25. Подсчитаем вероятность 20 попаданий при 24 и 25 выстрелах:

P24 20 P25 20 .

Для того чтобы наивероятнейшее число попаданий было равно 20, нужно провести либо 24, либо 25 выстрелов, причем вероятности ровно 20 попаданий при 24 и 25 выстрелах равны.

ЗАДАЧИ К РАЗДЕЛУ VII

1. Вероятность того, что денежный приемник автомата при опускании монеты сработает неправильно, равна 0,03. Найдите наиболее вероятное число случаев правильной работы автомата, если будет опущено 150 монет.

2.Перерасход горючего в течение рабочего дня наблюдается в среднем по парку у 20 % машин. Найдите вероятность того, что из десяти вышедших на линию машин перерасход горючего произойдет не менее чем у трех машин.

3.Каждый билет лотереи независимо от остальных билетов выигрывает с вероятностью 0,001. У меня 20 билетов. Чему равна вероят-

ность того, что я выиграю:

1)хотя бы по одному билету,

2)не менее, чем по двум билетам?

4. Вероятность попадания стрелка в десятку равна 0,7, в девятку – 0,3. Чему равна вероятность того, что при трех выстрелах стрелок наберет не менее 29 очков?

50