Тер.Вер методичка

б) расстояние от точки А до ближайшей стороны квадрата превосходит х.

18. В любые моменты промежутка времени T равновозможны поступления в приемник двух сигналов. Приемник будет забит, если разность между моментами поступления сигналов будет меньше . Найти вероятность того, что приемник будет забит.

19. Начерчены пять концентрических окружностей, радиусы которых равны соответственно kr (k = 1, 2, 3, 4, 5). Круг, радиусом r, кольцо с внешним и внутренним радиусами 5r и 3r заштрихованы. В круге радиусом 5r наудачу выбрана точка. Определить вероятность попадания этой точки: а) в круг радиусом 2r; б) в заштрихованную область.

20. По радиоканалу в течение промежутка времени (0;1) передаются два сигнала длительностью T < 1/2. Каждый из них с одинаковой возможностью начинается в любой момент интервала (0; 1 – T). Если сигналы перекрывают друг друга хотя бы частично, оба они искажаются и приняты быть не могут. Найти вероятность того, что сигналы приняты без искажений.

21.На отрезке длиной l наудачу выбраны две точки. Какова вероятность того, что расстояние между ними меньше kl, где 0 < k < l ?

22.На отрезке AB длиной l наудачу поставлены две точки L и M. Найти вероятность того, что точка L будет ближе к точке M, чем к

точке A.

23. В интервале времени [0, T] в случайный момент времени u появляется сигнал длительностью . Приемник включается в случайный момент времени [0, T] на время t. Найдите вероятность обнаружения сигнала приемником.

24. Плоскость разграфлена параллельными прямыми, находящимися друг от друга на расстоянии 2а. На плоскость наудачу брошена монета радиусом r < a. Найти вероятность того, что монета не пересечет ни одной из прямых.

25. Наудачу взяты два положительных числа – x и y, каждое из которых не превышает двух. Найти вероятность того, что произведение xy будет не больше единицы, а частное у/х не больше двух.

31

Р а з д е л V

УСЛОВНЫЕ ВЕРОЯТНОСТИ. ВЕРОЯТНОСТИ СУММ И ПРОИЗВЕДЕНИЙ СОБЫТИЙ

Вероятность суммы двух совместных событий:

P A B P A P B P AB .

Вероятность суммы трех совместных событий:

P A B C P A P B P C

P AB P AC P BC P ABC .

Вероятность суммы n несовместных событий:

Пример 1. Из колоды в 52 карты вытаскивается одна карта. Какова вероятность того, что это будет либо дама, либо карта пиковой масти?

Решение. Рассмотрим события А = {извлечена дама} и В = {извлечена карта пиковой масти}. Нас интересует сумма этих двух событий А + В = {извлечена либо дама, либо карта пиковой масти}.

32

P(A + B) = P(A) + P(B)–P(AB), где AB = {извлечена пиковая дама}.

P A 524 , P B 1352 (13 одинаковой масти), P AB 521 .

P A B P A P B P AB 524 1352 521 1652 134 .

Пример 2. В ящике 10 красных и 6 синих пуговиц. Вынимаются наугад две пуговицы. Какова вероятность того, что они будут одноцветными.

Решение. Нас интересует событие A = {вытащенные пуговицы одноцветные}. Представим событие A как сумму двух несовместных событий: A = A1 + A2, где A1 = {обе пуговицы красные}; A2 = {обе пуговицы синие}.

Так как события несовместны, то P(A) = P(A1) + P(A2).

Представим A1 и A2 как произведение двух событий: A1 = B1B2; A2 = C1C2, где B1 = {первая пуговица красная}, B2 = {вторая пуговица красная}, С1 = {первая пуговица синяя}, С2 = {вторая пуговица

синяя}.

Тогда P(A1) = P(B1)P(B2B1); P(A2) = P(C1)P(C2C1).

P B1 1016 85 ; P B2 | B1 159 53 – вероятность того, что вторая пуговица красная, если точно известно, что первая пуговица тоже красная.

Пример 3. Производится три независимых выстрела по мишени. Вероятности попадания в мишень при первом, втором и третьем выстрелах соответственно равны p1, p2, p3. Найти вероятность того, что в мишень произойдет ровно два попадания.

Решение. Запишем событие, вероятность которого нас интересует: A = {ровно два попадания}.

33

Событие A представим в виде трех несовместных события: A = A1 +

+ A2 + A3, где

A1 = {попал; попал; промах}; A2 = {попал; промах; попал}; A3 = = {промах; попал; попал}.

Каждое из событий Ai можно представить как произведение трех независимых событий:

B1 = {попадание при I выстреле}; B1 = {промах при I выстреле}; B2 = {попадание при II выстреле}; B2 = {промах при II выстреле}; B3 = {попадание при III выстреле}; B3 = {промах при III выстреле}.

P B3 1 p3 .

Поскольку события Bi независимы, то

P A1 P B1B2 B3 P B1 P B2 P B3 p1 p2 1 p3 , P A2 p1 1 p2 p3 ; P A3 1 p1 p2 p3 .

Так как события Ai несовместны, то

P A P A1 A2 A3 P A1 P A2 P A3p1 p2 1 p3 p1 1 p2 p3 1 p1 p2 p3.

Пример 4. Одна торпеда попадает в корабль с вероятностью 1/2. Какова вероятность того, что 4 торпеды потопят корабль, если для его потопления достаточно попадания одной торпеды?

Решение. A = {корабль потоплен}. Будем искать вероятность противоположного события A = {корабль не потоплен}. Введем дополнительные события: Bi = {i-я торпеда попала в цель (i = 1,2,3,4.)}. Bi = {i-я торпеда не попала в цель (i = 1, 2, 3, 4.)}.

P Bi 12 , P Bi 1 P Bi 12 .

Корабль будет потоплен, если в него попадет хотя бы одна торпеда. Сформулируем фразу противоположного смысла: корабль не будет потоплен, если в него не попадет ни одной торпеды. Таким образом,

34

A B1 B2 B3 B4 . Поскольку события Bi независимы, то будут независимы и противоположные к ним события, и тогда

P A P B1 P B2 P B3 P B4 12 12 12 12 161 ,

P A 1 P A 1 161 1615 .

Замечание. Если в задаче встречается формулировка «хотя бы один…», то удобнее перейти к противоположному событию, смысл которого «ни одно-

го…».

ЗАДАЧИ К РАЗДЕЛУ V

1. Стрелок выстрелил три раза по удаляющейся цели. Вероятность попадания в нее в начале стрельбы равна 0,8 и после каждого выстрела уменьшается на 0,1. Найти вероятности событий:

а) все три раза промах; б) хотя бы одно попадание; в) два попадания.

2.Батарея, состоящая из K орудий, ведет огнь по группе, состоящей из L самолетов (K L). Каждое орудие выбирает себе цель случайно и независимо от других. Найти вероятность того, что все K орудий будут стрелять по одной и той же цели.

3.Цифры 1, 2, 3, 4, 5 располагаются в ряд в случайном порядке.

Какова вероятность того, что первой окажется четная, а последней нечетная цифра?

4. Два стрелка сделали по одному выстрелу по мишени. Вероятность попадания для одного стрелка равна 0,7, для другого – 0,6. Найти вероятности событий:

а) только один из стрелков попал в мишень; б) хотя бы один из стрелков попал в мишень; в) оба стрелка поразили мишень; г) ни один из стрелков не попал в мишень;

д) хотя бы один из стрелков не попал в мишень.

5. Студент пошел на экзамен, зная лишь 20 из 25 вопросов программы, и получил 2 вопроса, наудачу выбранных из 25. Найти вероятность того, что студент знает оба этих вопроса.

35

6.Вероятность попадания в мишень при одном выстреле для одного стрелка равна р, для второго 0,7. Вероятность ровно одного попадания при одном выстреле обоих стрелков равна 0,38. Найти р.

7.Три стрелка, у которых вероятности попадания в мишень рав-

ны соответственно 0,7, 0,8 и 0,6, делают по одному выстрелу в одну и ту же мишень. Найти вероятность того, что:

а) мишень будет поражена более одного раза; б) мишень будет поражена не более одного раза.

8.В урне лежат 5 черных шаров, 4 красных и 3 белых. Последовательно вынимают три шара, причем каждый шар возвращается в урну перед тем, как вынимается следующий. Найти вероятность того, что первый шар окажется черным, второй – красным, третий – белым.

9.Студент сдает экзамен до первой удовлетворительной оценки, но не более трех раз. Вероятность сдать экзамен с первой попытки

равна 0,5. Вероятность сдать экзамен со второй попытки (после неудавшейся первой) равна 0,7, с третьей (после неудавшихся первой и второй) 0,7. Какова вероятность: а) сдать экзамен? б) провалить экзамен?

10.Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго 0,8. Найти вероятность того, что при одном залпе в мишень попадет только один из стрелков.

11.По железнодорожному мосту, независимо один от другого, производят серийное бомбометание три самолета. Каждый самолет сбрасывает одну серию бомб. Вероятность попадания хотя бы одной

бомбы из серии для первого самолета равна 0,2, для второго 0,3, для третьего 0,4. Найти вероятность того, что мост будет разрушен, если для разрушения достаточно хотя бы одного попадания.

12. Определить, какова вероятность, что все члены группы, состоящей из трех лиц разного возраста, проживут ближайшие 10 лет, если вероятность прожить 10 лет для первого лица равна 0,95, для второго лица 0,93 и для третьего 0,89.

13. Три стрелка независимо друг от друга стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0,75, для второго – 0,8, для третьего 0,9. Определить вероятность того, что все три стрелка одновременно попадут в цель.

14. В цехе работают две мясорубки. Цех прекращает работу досрочно при поломке одной из мясорубок. Вероятность поломки каждой 0,2 и 0,3 соответственно. Найти вероятность того, что цех прекратит работу досрочно.

36

15.Монета подбрасывается до тех пор, пока не выпадет герб. Какова вероятность того, что монету придется подбрасывать: а) ровно 5 раз; б) не менее 5 раз; в) не более 5 раз?

16.Игральная кость брошена пять раз. Найти вероятность появления одной и более «1».

17.Куплены два холодильника. Вероятность того, что каждый из

них выдержит гарантийный срок службы равна 0,9. Найти вероятность того, что в течение гарантийного срока:

а) оба холодильника не потребуют ремонта; б) только один из них потребует ремонта; в) хотя бы один не потребует ремонта.

(Холодильники выходят из строя независимо друг от друга.)

18. Игра состоит в набрасывании колец на колышек. Игрок получает 6 колец и бросает их до первого попадания. Вероятность попадания при каждом броске равна 0,1 и не зависит от результата предыдущих бросков. Найти вероятность того, что хотя бы одно кольцо останется неизрасходованным.

19. Из букв разрезной азбуки составили слово КОМБИНАТОРИКА. Не умеющий читать ребенок перемешал буквы этого слова и составил из них «слово» из четырех букв. Какова вероятность того, что этим словом оказалось слово кино?

20.В случайном порядке в ряд располагают 5 белых, 7 черных и 3 оранжевых шара. Найдите вероятность того, что на 1-м и 5-м местах

вэтом ряду будут белые шары, а на 15-м месте – оранжевый шар.

21.Студент пришел на зачет, зная ответы на 24 из 30 вопросов.

Какова вероятность сдать зачет, если после отказа отвечать на вопрос преподаватель задает еще один вопрос? Зачет выставляется за один правильный ответ.

22. Вероятность хотя бы одного попадания в мишень при трех выстрелах равна 0,875. Выстрелы независимы, вероятность попадания при каждом выстреле одинакова. Найти вероятность попадания при одном выстреле.

23.В двух урнах находятся шары, отличающиеся только цветом.

Впервой урне 5 белых шаров, 11 черных и 8 красных, а во второй соответственно 10, 8 и 6. Из обеих урн наугад извлекают по одному ша-

ру. Найти вероятность того, что: а) оба шара одного цвета; б) хотя бы один шар белый.

37

24.Для того чтобы сбить самолет, достаточно одного попадания. Было сделано три выстрела с вероятностями попадания 0,1; 0,2 и 0,4 соответственно. Какова вероятность того, что самолет сбит?

25.Серия послематчевых пенальти состоит из 10 ударов. На момент нанесения семи ударов выигрывает 1-я команда со счетом 3:2 (первый удар наносила 1-я команда). Вероятность точно пробитого

пенальти 1-й командой 0,6; 2-й – 0,8. Найти вероятность того, что на момент нанесения 10 ударов 1-я команда не проиграет.

Р а з д е л VI

ФОРМУЛЫ ПОЛНОЙ ВЕРОЯТНОСТИ И БАЙЕСА

Формула полной вероятности

Предположим, нам нужно определить вероятность события A. Опыт может закончиться одной из гипотез H1, H2, …, Hn, вероятность которых P(Hi) нам известна (гипотезы должны образовывать полную груп-

n

пу несовместных событий: Hi H j , если i j, Hi ). Вероятно-

i 1

сти появления события A при условии наступления каждой гипотезы нам известны: P(A|Hi). Тогда вероятность события A вычисляется по формуле полной вероятности

n

P A P Hi P A | Hi .

i 1

Пример 1. В тире имеется пять ружей, вероятности попадания из которых равны соответственно 0,5; 0,6; 0,7; 0,8 и 0,9. Определить вероятность попадания при одном выстреле, если стреляющий берет одно из ружей наудачу.

Решение. A = {стрелок попал}. Введем гипотезы: Hi = {стрелок выбрал i-е ружье (i = 1, 2, 3, 4, 5)}. Очевидно, эти события несовместны (стрелок может выбрать только одно из ружей) и образуют полную

38

группу событий (стрелок обязательно выберет одно из этих пяти ружей). Найдем вероятности гипотез. Так как шансы быть выбранным у каждого ружья одинаковы, то P(Hi) = 1/5 = 0,2 (i = 1, 2, 3, 4, 5). Вероятности попадания в цель при выборе i-го ружья заданы по условию

задачи: P(A|H1) = 0,5; P(A|H2) = 0,6; P(A|H3) = 0,7; P(A|H4) = 0,8; P(A|H5) = 0,9. Тогда

5

P A P Hi P A | Hi

i 1

0, 2 0,5 0, 2 0,6 0, 2 0,7 0, 2 0,8 0, 2 0,9 0,7.

Пример 2. При помещении в урну n шаров (из них m белых, остальные черные) один шар затерялся. Цвет его неизвестен. Теперь в урне осталось n–1 шаров. Какова вероятность вытащить белый шар?

Решение. A = {вытащенный шар – белый}.

Если бы мы точно знали цвет утерянного шара, то вычислить вероятность события A не составило бы труда. Введем следующие гипотезы: H1 = {утерянный шар белый}, H2 = {утерянный шар черный}. Эти два события действительно являются гипотезами, поскольку они несовместны (утерянный шар не может быть одновременно белым и черным) и образуют полную группу событий (утерянный шар может быть либо белым, либо черным).

Замечание: поскольку цвет утерянного шара неизвестен, то вероятность вытащить белый шар не изменится.

Пример 3. В первой партии деталей содержится N деталей, из которых n – бракованные. Во второй партии деталей содержится M деталей, из которых m – бракованные. Из первой партии берут K деталей (K<N), а из второй партии L деталей (L<M) и образуют новую партию из K + L деталей. Из новой партии берут одну деталь. Какова вероятность, что эта деталь бракованная?

39

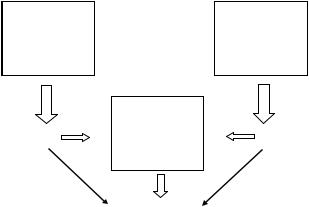
Решение

A = {выбранная деталь бракованная} Введем гипотезы:

H1 = {деталь ранее принадлежала I партии}; H2 = {деталь ранее принадлежала II партии}.

Найдем вероятность первой гипотезы. В новой III партии K деталей из I партии и L деталей из II партии. Тогда вероятность того, что взятая

Найдем вероятность события A при наступлении каждой гипотезы. P(A|H1) – вероятность того, что извлеченная из III партии деталь

бракованная, если мы точно знаем, что она ранее принадлежала I партии (т. е. это одна из K деталей). Таким образом, задача определения P(A|H1) сводится к примеру 4 раздела 3: