Тер.Вер методичка

11.Сколькими способами группу из 12 юношей и 8 девушек можно разбить на две группы по 10 человек так, чтобы в каждой из образовавшихся групп оказалось по 4 девушки?

12.Имеется 6 видов бокалов и рюмок, которые ставятся на стол на

званом ужине: бокал для шампанского, лафитная рюмка, рюмка для рейнвейна, мадерная рюмка, фужер, водочная рюмка. Все бокалы и рюмки устанавливают в один ряд. Сколько способов их постановки существует? (Правилами этикета пренебречь.)

13.Сколькими способами можно упорядочить множество {1; 2;… …; n} так, чтобы числа 1; 2; 3 стояли рядом и в порядке возрастания?

14.Жил-был странный правитель. Решил он своих подданных различать не по именам, а по зубам. Себе все 32 зуба оставил, как и были, белыми. Ближайшим подданным повелел один зуб на разных позициях

окрасить в черный цвет, чтобы их отличать. Далее шли вассалы с двумя черными зубами на разных позициях, и так далее. В самых низших слоях были люди с одним белым зубом на разных местах и был один только с черными. Сколько было подданных у правителя?

15. Из вершины прямого угла внутри него проведено 5 лучей. Сколько острых углов образовалось при этом? (Углы образуются не только между смежными углами, но и между любой парой лучей, включая стороны прямого угла.)

16. В коробке 5 карандашей разного цвета: красного, оранжевого, желтого, зеленого, розового. Ребенку нужно раскрасить 5 картинок. Он наугад берет один из карандашей, раскрашивает им первую картинку, а потом кладет карандаш обратно в коробку. Затем точно так же раскрашивает остальные 4 картинки. Сколько существует различных вариантов раскраски 5 картинок?

17. Из цифр 1, 2, 3, 4, 5 составляются всевозможные пятизначные числа без повторяющихся цифр.

а) сколько чисел будет оканчиваться комбинацией 41? б) сколько получится четных и сколько нечетных чисел?

18.Сколько трехзначных чисел без повторяющихся цифр можно записать, используя цифры (ноль на первом месте стоять не может):

а) 1; 2; 3; 4; 5; б) 0; 1; 2; 3; 4; 5?

19.На собрании членов кооператива присутствуют 20 человек.

Сколькими способами из присутствующих можно выбрать: а) правление кооператива в составе 5 человек; б) председателя правления, его заместителя и бухгалтера?

11

20.Правление коммерческого банка выбирает из 8 кандидатов трех человек на различные должности (все 8 кандидатов имеют равные шансы). Сколько всевозможных групп по 3 человека (на различные должности) можно составить из 8 кандидатов?

21.Имеется пять видов конвертов без марок и четыре вида марок одного достоинства. Сколькими способами можно выбрать конверт с

маркой для посылки письма?

22.Группа студентов из 30 человек решила обменяться фотокарточками. Сколько фотокарточек понадобится для этого?

23.Автоматическая система состоит из пяти параллельно соединенных узлов. По тем или иным причинам за время Т каждый из этих

узлов, независимо от остальных узлов, может выйти из строя. Сколько существует различных вариантов состояния системы к моменту времени Т? Сколько среди них таких, для которых хотя бы

один узел оказывается не вышедшим из строя? 24. Сколькими способами можно 20 шахматистов разбить на две

группы по 10 человек так, чтобы двое наиболее сильных шахматиста оказались:

а) в разных группах; б) в одной группе?

25. Сколько имеется четырехзначных чисел, у которых каждая следующая цифра меньше предыдущей? (Подсказка: любые k различных цифр можно расположить в порядке возрастания или в порядке убывания единственным образом).

Р а з д е л II

ОПЕРАЦИИ НАД СЛУЧАЙНЫМИ СОБЫТИЯМИ

Суммой (объединением) двух событий A и B называют событие, в результате которого произойдет хотя бы одно из событий A или B. Эту операцию обозначают A + B или A B.

Пример 1. Бросается игральный кубик. События A = {выпадение 1, 2 или 3 очков}; B = {выпадение четного числа очков}. Тогда A + B = = {выпадение 1, 2, 3, 4 или 6 очков}.

12

Пример 3. Рассмотрим пример 1. A – B = {выпадение 1 или 3 очков}, B – A = {выпадение 4 или 6 очков}.

Противоположным событием по отношению к событию A, назы-

вают событие A , состоящее в не появлении A.

Пример 4. Рассмотрим пример 1. A = {выпадение 4, 5 или 6 очков}, B = {выпадение нечетного числа очков}.

A

A

13

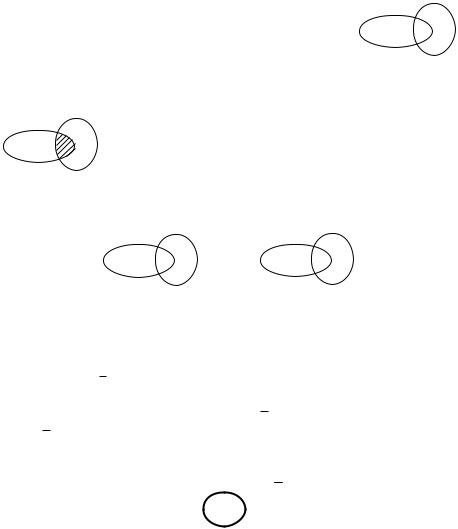
Пример 5. На плоскости произвольным образом рисуется точка. События A = {точка попала в круг A}, B = {точка попала в круг B}.

Какой смысл имеют события A , B , A + B, AB, AB ?

Пример 6. Из таблицы чисел взято одно число. Событие A = {выбранное число кратно 5}, B = {данное число оканчивается нулем}. Что

означают события A – B и A B ?

Решение. Число, кратное 5, должно заканчиваться либо на 0, либо на 5. Тогда

A – B = {данное число оканчивается на цифру 5}, B = {данное число не оканчивается на ноль},

A B = {данное число оканчивается на цифру 5}, т. е. A – B и A B одно и то же событие.

Пример 7. Пусть A, B и C – три произвольных события. Записать выражение для заданных событий:

1)произошло только событие A;

2)произошли все три события;

3)произошло, по крайней мере, одно из событий;

4)произошло, по крайней мере, два события;

5)произошло одно и только одно событие;

6)не произошло ни одного события;

7)произошло не более двух событий.

Решение. Ответим последовательно на все 7 вопросов:

1)A B C или A – B – C

2)ABC

3)A + B + C

4)AB + AC + BC

5)ABC ABC A BC

14

6)A B C или A B C

7)A B B C A C

Пример 8. Бросаются две игральные кости (кубика). События A = {сумма очков равна 5}, B = {хотя бы на одной из костей выпала

единица}. Описать события AB и A B .

Решение. Запишем все исходы составляющие события A и B:

A = {1:4; 2:3; 3:2; 4:1}, B = {1:i; i:1} (i = 1,2,3,4,5,6). AB = {1:4; 4:1} =

= {на одной из костей выпала единица, на другой четверка}. B = {ни

на одной из костей не выпала единица}, A B = {2:3; 3:2} = {на одной из костей выпала двойка, на другой тройка}.

Пример 9. Цепь состоит из системы контактов. Событие Аi = = {контакт Кi замкнут (i = 1;2;3;4)}. Записать события: а) цепь замкнута; б) цепь разомкнута.

Решение.

а) A1 A2 A3 A4 A5 б) A1 A2 A3 A4 A5

К3

Событие называется невозможным, если в результате случайного эксперимента оно не произойдет ни при каких обстоятельствах. Обозначается символом .

Пример невозможного события – выпадение двух и четырех очков при одном броске игральной кости.

Событие называется достоверным, если в результате опыта оно обязательно произойдет. Обозначается символом .

Пример достоверного события – выпадение любого из шести очков при одном броске игральной кости.

15

Свойства операций над событиями:

1) A + B = B + A; 2) AB = BA; 3) A A ; 4) A = A; 5) AA ; 6) A A ; 7) A B AB ; 8) (A + B)C = AC + BC; 9) A B A B ;

10) AB A B .

Свойства 1) – 7) непосредственно следуют из определения операций над событиями.

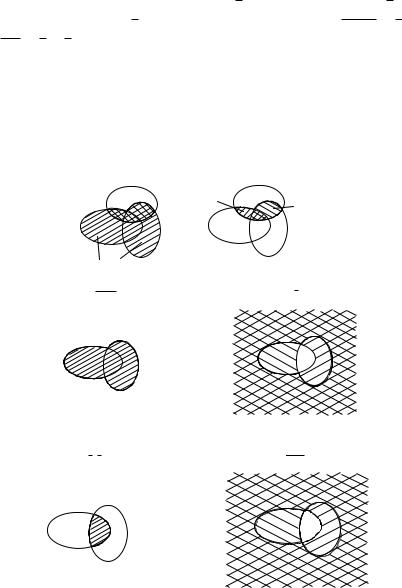
Покажем свойство 8). Удобно использовать графический метод, так называемые диаграммы Эйлера. События представляются как множество точек на плоскости. Нужно показать, что множество левой части равенства совпадает с множеством правой части.

=

10)

16

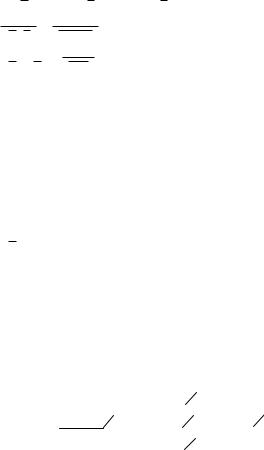
Пример 10. Упростить заданные выражения.

1)A B B AB A AB A B A A ,

2)A B A B A B ,

3)A B AB AB ,

4)A B AB AAB BAB AB AB AB .

ЗАДАЧИ К РАЗДЕЛУ II

1.Производится два выстрела по мишени. Образуют ли полную группу следующие группы событий: А = {хотя бы одно попадание};

В= {хотя бы один промах}. Объяснить.

2.Бросаются две игральные кости. События A = {сумма очков равна 5}, B = {хотя бы на одной из костей выпала двойка}. Опишите со-

бытие AB .

3.Опыт состоит в подбрасывании двух монет. Являются ли несовместными следующие события: А = {появления герба на первой монете}; В = {появления цифры на второй монете}. Объяснить.

4.Цепь состоит из системы контактов. Событие Аi = {контакт Кi замкнут (i = 1;2;3;4;5)}. Записать события:

а) цепь замкнута;

б) цепь разомкнута.

5.Производится два выстрела по мишени. Являются ли несовместными следующие события: А = {ни одного попадания}; В = {одно попадание}; С = {два попадания}.

6.Рабочий изготовил n деталей. События Аi = {i-я изготовленная деталь имеет дефект (i = 1; 2; 3; 4)}. Выразить через события Аi сле-

дующие события: В = {ни одна из деталей не имеет дефектов}, С = {хотя бы одна имеет дефект}.

17

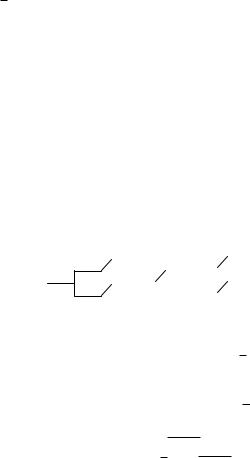
7. Прибор состоит из двух блоков первого типа и трех блоков второго типа. Событие Аi = {исправен i-й блок первого типа (i = 1;2)}, Вk = {Исправен k-й блок второго типа (k = 1; 2; 3)}. Прибор работает, если исправен хотя бы один блок первого типа и не менее двух блоков второго типа. Выразить событие С = {прибор работает} через события

Аi и Вk.

8. Подбрасываются три монеты. События А = {выпал хотя бы один герб}; В = {выпали ровно две цифры}. Что означают события:

а) АВ; б) A B .

9. Когда возможно равенство АВ = А?

10. Мишень состоит из десяти кругов, ограниченных концентрическими окружностями rk (k = 1; 2;3;…;10), причем r1 < r2 < r3 <…< r10. События Ak = {попадание в круг радиуса rk (k = 1; 2; 3; …; 10)}. Что

11.События: А = {хотя бы один из трех проверяемых приборов бракованный}; В = {все приборы доброкачественные}. Что означают события: а) А + В; б) АВ?

12.Цепь состоит из системы контактов. Событие Аi = {контакт Кi

замкнут (i = 1; 2; 3; 4; 5)}. Записать события: а) цепь замкнута; б) цепь разомкнута.

13. Из таблицы случайных чисел наудачу взято одно число. События А = {выбранное число делится на 5}; В = {данное число оканчива-

ется нулем}. Что означают события: A B и AB ?

14. События: А = {хотя бы одно из имеющихся четырех изделий бракованное}; В = {бракованных изделий среди них не менее двух}.

Что означают противоположные события: A и B ?

15.Когда возможно равенство: A B AB ?

16.Совместны ли события A и A B ?

17. Доказать, что события A , AB и A B образуют полную группу событий.

18

18.Два шахматиста играют одну партию. События: А = {выиграет первый игрок}, В = {выиграет второй игрок}. Какое событие следует добавить к указанной совокупности, чтобы получилась полная группа событий?

19.По самолету запущено четыре ракеты. События Аi = {i-я ракета попала в цель (i = 1; 2; 3; 4)}. Для поражения самолета достаточно по-

падания одной ракеты. Записать событие (выразить через события Аi)

В= {самолет не поражен}.

20.Бросается игральный кубик. События А = {выпало нечетное

число}; В = {выпавшее число не меньше 3}. Через события А и В выразить событие С = {на кубике выпала 2}.

21.Упростить выражение A (B C)(B C)(B C) .

22.Из колоды вытаскивают две карты. События A = {обе карты пиковой масти}, B = {ни одна из них не туз}. Что означает событие

A – B?

23.Опыт состоит в подбрасывании двух монет. Образуют ли полную группу следующие группы событий: А = {появления двух гербов};

В= {появления двух цифр}. Объяснить.

24.Стрелок производит три выстрела по мишени. Событие Аi = = {попадание в мишень при i-м выстреле (i = 1; 2; 3)}. Выразить через

Аi событие В = {хотя бы два попадания в мишень при трех выстрелах}.

Р а з д е л III

НЕПОСРЕДСТВЕННЫЙ ПОДСЧЕТ ВЕРОЯТНОСТЕЙ

Существуют опыты, обладающие симметрией возможных исходов (случаев). О самом опыте говорят, что он сводится к схеме случаев. Случаи должны удовлетворять трем следующим условиям:

1) они должны быть несовместны (т.е. два случая не могут произойти одновременно);

19

2)они должны образовывать полную группу событий (т.е. опыт должен заканчиваться одним из случаев);

3)они должны быть равновозможными (т.е. возможности появления ни одного из случаев нельзя отдать предпочтение).

Вероятность события А определяется как отношение числа случаев, составляющих событие А, к общему числу случаев:

P A mNA .

Пример 1. В урне находится a белых, b черных шаров. Наугад берут один шар. Найти вероятность событий A = {шар белый} и B = {шар черный}.

Решение: Пронумеруем шары, чтобы их различать. Пусть № 1, 2, …, a – номера белых шаров, № a + 1, a + 2, …, a + b – номера черных шаров. Возьмем за случай событие = {изъят шар с № i} (i = 1, 2, …, a + b). Очевидно, эти события удовлетворяют всем вышеперечисленным трем свойствам. Всего случаев a + b. Число случаев, благоприятных событию A, равно a, благоприятных событию B, равно b. Таким образом,

N = a + b, mA = a, mB = b.

Пример 2. В урне лежат a белых, b черных шаров. Из урны вынимают сразу два шара. Найти вероятность того, что один из шаров будет белый, а другой черный.

Решение. Найдем вероятность события A = {один из вынутых шаров белый, другой черный}. Пронумеруем шары так же, как в преды-

дущей задаче. Рассмотрим событие = {вытащили два шара с номерами i и j} (i, j = 1, 2, …, a + b, i ≠ j). Очевидно они образуют полную группу несовместных событий. Эти события также равновозможные. Действительно, шансы вытащить шары с номерами, к примеру, «1» и «3», точно такие же, как и у шаров с номерами, к примеру, «2» и «6».

Таким образом, события можно считать случаями. Подсчитаем общее число случаев. В данной задаче случаи – это комбинации, состоящие из двух шаров, выбранных из общего числа шаров a + b. Поскольку порядок, в котором были выбраны два шара один за другим, здесь не важен, то эти комбинации отличаются друг от друга только соста-

20