
Лабораторная работа № 7
ПОСТРОЕНИЕ ГРАФИКОВ
Цели работы:
1.Построение графиков функций.
2.Получение практических навыков работы в диалоговом режиме.
ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ
Одно из достоинств системы MATLAB – обилие средств графики, начиная от команд построения простых графиков функций одной переменной в декартовой системе координат и кончая комбинированными и презентационными графиками с элементами анимации.
1. Построение графиков отрезками прямых
Для отображения функции одной переменной у (х) используются графики в декартовой (прямоугольной) системе координат. При этом обычно строятся две оси – горизонтальная X и вертикальная Y, и задаются координаты х и у, определяющие узловые точки у (х).
Эти точки соединяются друг с другом отрезками прямых, то есть при построении графика осуществляется линейная интерполяция для промежуточных точек. Поскольку MATLAB – матричная система, совокупность точек у (х) задается векторами X и Y одинакового размера.
Команда plot служит для построения графиков функций в декартовой системе координат. Эта команда имеет ряд параметров, рассматриваемых ниже.
¾ plot (X, Y) строит график функции у (х), координаты точек (х, у) которой берутся из векторов одинакового размера Y и X.
Если X или Y – матрица, то строится семейство графиков по данным, содержащимся в матрице.
Пример 1
Приведенный ниже пример (рис. 10) иллюстрирует построение графиков двух функции – sin (x) и cos (х), данные которых содержатся в матрице Y, а значения х хранятся в векторе X:
>> x = [0 1 2 3 4 5 6]
>>y = [sin (x); cos (x)];
>>plot (x, y)
Вданном случае отчетливо видно, что график состоит из отрезков,
иесли вам нужно, чтобы отображаемая функция имела вид гладкой кривой, необходимо увеличить количество узловых точек. Расположение их может быть произвольным.
34
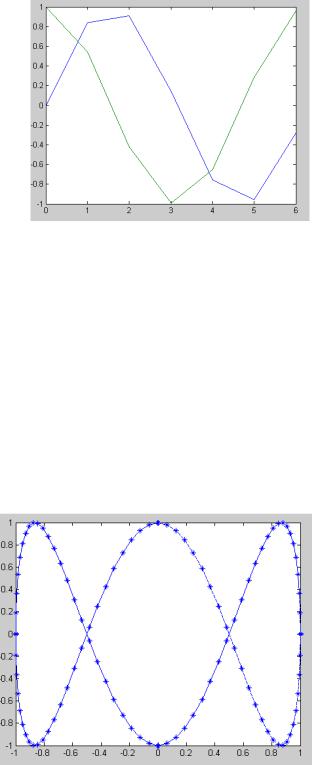
Рис. 10. Построение графиков функций sin (x), cos (x) отрезками прямых
¾ plot(Y) строит график y (i), где значения Y берутся из вектора Y, a i представляет собой индекс соответствующего элемента. Если Y содержит комплексные элементы, то выполняется команда plot (real (Y), imag (Y)). Во всех других случаях мнимая часть данных игнорируется.
Пример 2
Построить график функции y = sin (x) + i * cos (3 * x), где аргумент х [-2 π ; 2 π] и изменяется с шагом 0,02 (рис. 11).
>>x = - 2 * pi : 0. 02 * pi : 2 *pi ;
>>y = sin (x) + i * cos (3 * x ) ;
>>plot (y)
>>plot (y , ' b : * ')
Рис. 11. График функции y = sin (x) + i * cos (3 * x)
Пример 3
Построить график функции параболы в интервале [1; 10] c шагом 1. Рассмотрим, как могут выглядеть задания.
–>> x = 1 : 1 : 10;
>>y = x .* x;
>>plot (x , y)
35
–>> x = 1 : 1 : 10;
>>y = x . ^ 2;
>>plot (x , y)
–>> for х = 1 : 10;
>>y (х) = х * х ; end
>>plot (y)
Пример 4
Построить график функции параболы в интервале [1 ; 20] c шагом 0, 1. Рассмотрим, как могут выглядеть задания.
–>> x = 1 : 0. 1 : 20;
>>y = x . ^ 2 ; plot (x, y)
–>> for i = 1 : 20;
>>x = 0. 1 * i ;
>>y (i) = x * x ; end
>>plot (Y)
¾plot (Х, Y, S) аналогична команде plot (X, Y), но тип линии графика можно задавать с помощью строковой константы S, которая задает цвет линии (табл. 7) или вид символа (табл. 8).
Таблица 7
|
Цвет линии |
|
Y – Желтый |
|
G – Зеленый |
M – Фиолетовый |
|
B – Синий |
C – Голубой |
|
W – Белый |
R – Красный |
|
K – Черный |
Таблица 8
Тип точки |
|
Тип линии |
. – Точка |
|
|
+ – Плюс |
- |
–Сплошная |
О – Окружность |
||
Х – Крест |
: |
–Двойной пунктир |
* – Звездочка |
- . –Штрих-пунктир |
|
S – Квадрат |
- - |
–Штриховая |
D – Ромб |
|
|
V –Треугольник (вниз) |
|
|
Итак, с помощью строковой константы S можно:
–изменять цвет линии;
–представлять узловые точки различными отметками (точка, окружность, треугольник);
–менять тип линии.
36
¾ plot (Xl, Yl, Sl, X2, Y2, S2, X3 ,Y3, S3,...) – эта команда строит на од-
ном графике ряд линий, представленных данными вида (Xi,Yi, Si), где Xi и Yi
– векторы или строки матрицы, a Si –задает цвет и тип точек или линий, из которых будет построен график.
При отсутствии указания на цвет линий и точек он выбирается автоматически из таблицы цветов (белый исключается).
Рассмотрим пример построения графиков трех функций с различным стилем представления каждой из них:
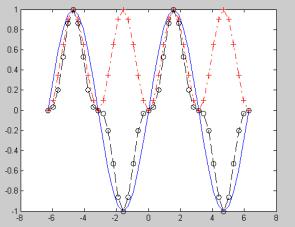
Пример 5
% Построение графиков трех функций со спецификацией линий каждого графика (рис. 12).
>>x = - 2 * pi : 0. 1 * pi: 2 * pi ;
>>y1 = sin (x);
>>y2 = sin (x). ^ 2;
>>y3 = sin (x). ^ 3;
>>plot (x, y1, ' – b ', x, y2, ' - . + r ', x, y3, ' – ok ')
Рис. 12. Графики трех функций со спецификацией линий каждого графика
–график функции yl строится сплошной синей линией;
–график у2 строится штрихпунктирной линией с точками в виде знака «плюс» красного цвета;
–график уЗ строится штриховой линией с кружками черного цвета.
2.Построение графиков в полярной системе координат
Вполярной системе координат любая точка представляется как конец радиус-вектора, исходящего из начала системы координат, имеющего длину
ри угол Q.
Для построения графика функции р(Q) используются приведенные ниже команды. Угол Q обычно меняется от 0 до 2π. Для построения графиков функций в полярной системе координат используются команды типа polar(...):
37
¾ polar (THETA, RHO) строит график в полярной системе координат, представляющий собой положение конца радиус-вектора длиной RHO
ис углом ТНЕТА;
¾polar (THETA, RHO, S) – аналогична предыдущей команде, но позволяет задавать стиль построения с помощью строковой константы S по аналогии с командой plot.
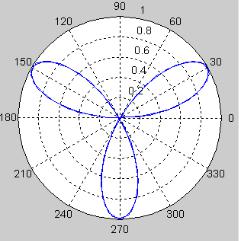
Пример 6
% График Polar(y) в полярной системе координат (рис. 13).
>>phi = 0 : 0. 1 : 2 * pi; r = sin (3 * phi) ;
>>polar (phi, r)
Рис. 13. График функции sin (3α) в полярной системе координат
3. Построение графиков векторов
Иногда желательно представление ряда радиус-векторов в их обычном виде, т.е. в виде стрелок, исходящих из начала координат и имеющих угол и длину, определяемые действительной и мнимой частью комплексных чисел, представляющих эти векторы.
Для этого служит группа команд compass:
–Compass (U, V) – строит графики радиус-векторов с компонентами (U, V), представляющими действительную и мнимую части каждого из ра- диус-векторов.
–Compass (Z) – эквивалентно Compass (real(Z),imag (Z)) ;
–Compass (U, V, LINESPEC) и Compass (Z, LINESPEC)- аналогичны представленным выше командам, но позволяют задавать спецификацию линий построения LINESPEC подобную описанной для plot.
Пример 7
% Построение радиус-векторов для вектора z, заданного комплексными числами (рис. 14).
>>z = [- 1 + 2i, -2 – 3i, 2 + 3i, 5 + 2i]
>>compass (z)
38
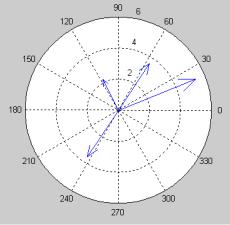
Рис. 14. Построение радиус-векторов
3.Трехмерные графики
3.1.Функция meshgrid для создание массивов трехмерной графики
Трехмерные поверхности обычно описываются функцией двух переменных z (x, у). Специфика построения трехмерных графиков требует не просто ряда значений x и y , то есть векторов x и y – она требует определения двумерных массивов X и Y — матриц. Для создания таких массивов служит функция meshgrid..В основном она используется совместно с функциями построения графиков трехмерных поверхностей. Функция meshgrid записывается в следующих формах:
–[X, Y] = meshgrid (x, y) преобразует область, заданную векторами х
иу, в массивы X и Y, которые могут быть использованы для вычисления функции двух переменных и построения трехмерных графиков. Строки выходного массива X являются копиями вектора х, а столбцы Y – копиями вектора у;
–[X, Y] = meshgrid (x) — аналогична [X, Y] = meshgrid (x, x);
–[X, Y, Z] = meshgrid (x, y, z) возвращает трехмерные массивы, используемые для вычисления функций трех переменных и построения трехмерных 3D-графиков.
3.2. Построение графиков трехмерных поверхностей
Команда plot3 (...) является аналогом команды plot (...). Она строит аксонометрическое изображение трехмерных поверхностей и представлена следующими формами:
¾plot3 (x, y, z) строит массив точек, представленных векторами х, у
иz, соединяя их отрезками прямых. Эта команда имеет ограниченное применение;
¾plot3 (X, Y, Z)- строит точки с координатами X(i,:), Y(i,:) и Z(i,:)
исоединяет их отрезками прямых, где X, Y и Z — три матрицы одинакового размера;
¾plot3 (X, Y, Z, S)- обеспечивает построения аналогичные предыдущей команде, но со спецификацией стиля линий и точек, соответствующей
39
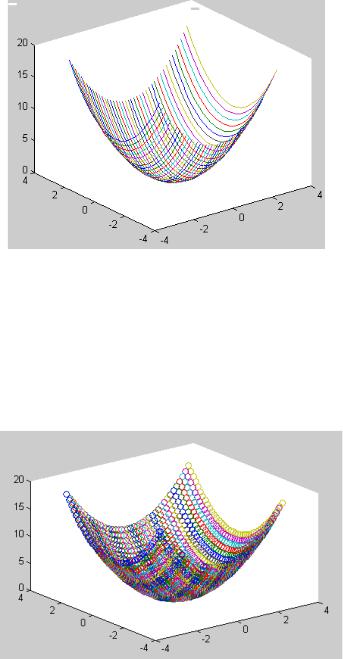
Пример 8
Рассмотрим пример построения трехмерной поверхности, описываемой функцией z (x, y) = x2 + y2 (рис. 15).
>>% Построение графика 3D поверхности линиями
>>[x, y] = meshgrid ([ - 3 : 0. 15 : 3 ]);
>>z = x . ^ 2 + y . ^ 2;
>>plot3 (x, y, z)
Рис. 15. График трехмерной поверхности
Пример 9
Построить график 3D поверхности (рис. 16).
>>% Построение графика 3Dповерхности цветными кружками
>>[x , y] = meshgrid ([ -3 : 0. 15 : 3]) ;
>>z = x . ^ 2 + y . ^ 2 ;
>>plot 3(x, y, z, ' o ')
Рис. 16. График трехмерной поверхности, построенный разноцветными кружками
3.3. Управление осями
Функция axis имеет несколько возможностей для настройки масштаба, ориентации и коэффициента сжатия.
41
