Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Лабораторные работы 5-6-7 MatLab.pdf

Скачиваний:

Добавлен:

27.03.2015

Размер:

936.17 Кб

Скачать

☆

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

u – переменная интегрирования,

а – нижний предел интегрирования, b – верхний предел интегрирования.

Продемонстрируем приемы вычисления интегралов в MATLAB на следующих примерах:

Пример 9

Вычислить интеграл: ∫a2 +dx( bx )2 ;

>> syms a b c % задаем символьные переменные

>> int (1 / a ^ 2 + ( b * x ) ^ 2) % вычисляем интеграл в символьном виде

ans =
1/ a / b * atan (b *	x /		a)
Пример 10	a / b
	a / b			dx
Вычислить интеграл	∫			dx		;
Вычислить интеграл	∫	a	2	+ ( bx )	2	;
	a	a		+ ( bx )
>> syms a b c	a					% задаем символьные переменные
>> syms a b c						% задаем символьные переменные

>> int (1 / a ^ 2 + (b * x) ^ 2, 0, a / b) % вычисляем интеграл в символь-

ном виде ans =

1 / 4 * pi / a / b

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Перечислите пакеты расширения МATLAB.

2.Как получить справку по командам пакета

3.Какая функция используется для создания символьных переменных

ислужит для обращения к стандартным функциям?

4.Какая команда используется для решения алгебраических уравнений?

5.Какая команда для упрощения алгебраических выражений?

6.Какая команда используется для вычисления сумм рядов?

7.Что необходимо сделать для вычисления производной функции?

8.Перечислите функции, служащие для вычисления интегралов в символьном виде.

ПРАКТИЧЕСКОЕ ЗАДАНИЕ

1.Ознакомиться с теоретическим материалом и ответить на вопросы.

2.Организовать ввод данных и вычисления в интерактивном режиме согласно заданиям.

3.ПротоколывыполненныхзаданийвМATLAB показатьпреподавателю.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

–Открыть окно программы МATLAB, используя соответствующий

ярлык

–Выполнить задания согласно указаниям, используя в случае необходимости help программы МATLAB.

Задание № 1

Решить алгебраические уравнения, используя команду solve:

x +8

−1;

x −3

2x2 −18

3 − x

x +1

;

x −1

x2 + 2x −3

x +3

c) 1 + x 6−1 = 5x−−27x ;

Задание № 2

Решить систему алгебраических уравнений, используя команду solve. Выбрать уравнение согласно своему варианту из табл. 3.

Таблица№3

Варианты заданий

Номер варианта			Система уравнений
1		2	−3xy +x	2	−x + y +9			=0,
	y
	y −x = 2.
2	(2x −6) / 3−(x −2) / 2 =2y,
	(3x −6) / 2 + y / 2 =x.
3	2x + y =1,
		2	−2xy −x2 =−28
	y
4		2	−xy =12 − y			2	,
	x
	x −2y =6.
5	(x −6) / 2 −( y +1) / 3=1,
	(2 − y)4 +(x −1) / 2 =2.
6	x − y =7,
		2	+ y2 =9 −2xy.
	x

7	1/ x −1/ y =−4 / 5,
	x − y =4.
8	4 /(x − y) +12(x + y) =3,
	8 /(x − y) +18(x + y) =−1.
9	3/(x − y) −4 /(x + y) =−1,
	9 /(x − y) −10 /(x + y) =8.
10	6 /(x − y) −8 /(x + y) =−2,
	9 /(x − y) −10 /(x + y) =8.
11	1/ x +4 / y =4,
	1/ e −2 / x =10.
12	2 / x +1/ y =4,
	1/ x −3/ y =9.
13	1/ x +1/ y = 7 /12,
	1/ x −1/ y =1/12.
14	1/ x −1/ y =3/ 8,
	x + y =12.
15	x + y =3,
		−x − y =2.
	x2 +3xy + y3
16	3x − y =10,
		− xy.
	x2 − y2 =20

Задание № 3

Упростить выражения, используя команду simplify:

+ 4

(2 −c)

p =

−

;

− 2

c +

− c

2c + c

p =

;

(x −1)(x −3)

(x −3)(x −5)

(x −5)(x −7)

6x −25

p =

3x −

: x −

x −4

x −

Задание № 4

Вычислить сумму ряда, используя команду symsum. Выбрать уравнение согласно своему варианту из табл. 4.

Таблица 4

Варианты заданий

Номер варианта	Вид функционального ряда
	∞	(−1)	2	k
1	s = ∑	(−1)		k
1	s = ∑	k (2k +1) 2			k
	k=1	k (2k +1) 2

s = ∑6

(−1)k

k=1

3k +1

s = ∑5

(k −1)2

k=2

(2k −1)

s = ∑

k=3

2 k

s = ∑7

(−1)n−1

k=1

(2k −1)

s = ∑5

(−1)2

k=1

2 k

∞

s = ∑

k (2k +1)

k=1

∞

s = ∑

(k +10)

k=1

∞

(−1)

s = ∑

(k +1)(k +2)

k=1

∞

s = ∑

k(k +1)(k +2)

k=1

∞

s = ∑

(k +1)(k +2)(k +3)

k=1

∞

(2k −1)

s = ∑

2 2

k=1

(k +1)

∞

s = ∑

k=2

−1

s = ∑9

−1

k=2

s = ∑9

−1

k=2

s = ∑5

(−1)k

k=1

5k +1

Задание № 5

Вычислить производную функции по х, используя команду diff. Выбрать функцию согласно своему варианту из табл. 5.

Таблица 5

Варианты заданий

Номер варианта	Функция для вычисления производной
1						ln x
1		x				1 + ln x
		x				1 + ln x

2		ln 2 x
2			x
			x

3		x e x Sin x
4						1
4			9 + x2
			9 + x2
5	1					Sin(				1	)
5		x2				Sin(					)
		x2								x
6			ArcSin										x
6			ArcSin									1 + x

7		xx			(1 + ln x)
8			x2 − 0,16
8						x
						x
9		e3x				+1
9		ex				+1
		ex				+1
10		ex			(1 +Sinx)
10				1 + Cosx
				1 + Cosx
11		Sinx ln (Tg x)

12								1
12		( x +1) x2 +1
13								1
13		(3Sin x + 2Cosx)2
14	(		ln x				) 3
14	(						) 3
				x
15									x
15		( x4 + 3x 2 + 2)
16				1				dx
16		x lg x						dx
		x lg x

Задание №6

Используя функцию int, подготовить и организовать вычисление опре-

деленного интеграла: y = ∫ f (x)dx .

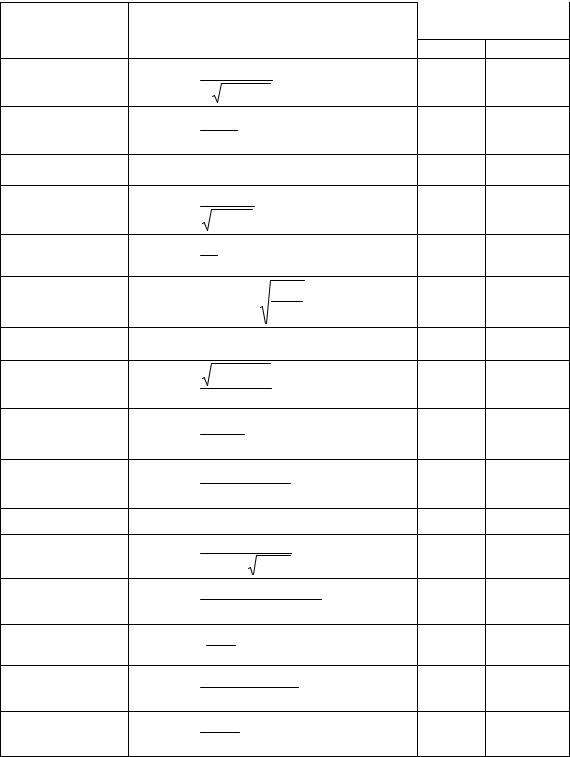
Подынтегральная функция f(x) определена и непрерывна на интервале
a <= x <= b. Вид подынтегральной функции f(x), а также интервал интегри-
рования [a, b] определяется номером варианта из табл. 6.
						Таблица 6
	Варианты заданий
						Пределы
Номер варианта	Подинтегральная функция f (x)				интегрирования
		ln x			a	b
1		ln x			1	3,5
1	x	1 + ln x			1	3,5
	x	1 + ln x
2	ln 2 x				1	4
2	x				1	4
	x
3	x e x		Sin x		0	1
4		1			0	2
4	9 + x2				0	2
	9 + x2
5	1	Sin( 1 )			1	2,5
	x2		x
6	ArcSin			x	0	3
6	ArcSin			1 + x	0	3
				1 + x
7	xx (1 + ln x)				1	3
8	x2 − 0,16				1	2
8		x			1	2
		x
9	e3x	+1			0	2
9	ex	+1			0	2
	ex	+1
10	ex (1 +Sinx)				0	1,5
10	1 + Cosx				0	1,5
	1 + Cosx
11	Sinx ln (Tg x)				1	1,5
12			1		0	0,75
12	( x +1) x2			+1	0	0,75
13			1		0	1
13	(3Sin x + 2Cosx)2				0	1
14	( ln x ) 3				1	2
	x		x
15			x			2
15	( x4 + 3x 2 + 2)					2
16	1		dx		2	3
16	x lg x		dx		2	3
	x lg x
				33

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
27.03.20152.23 Mб13Лабораторная работа_1.doc
#
04.12.20182.15 Mб44лабораторная №3.doc
#
20.08.2019162.3 Кб5Лабораторные работы для заочников.doc
#
03.05.2015421.38 Кб89ЛАБОРАТОРНЫЕ ПО ФОРТРАНУ №8.DOC
#
01.04.2025223.74 Кб0Лабораторные работы 2013 ( группы АБ).doc
#
27.03.2015936.17 Кб68Лабораторные работы 5-6-7 MatLab.pdf
#
27.03.2015760.46 Кб66Лабораторные работы ММП.pdf
#
01.05.2025479.97 Кб0Лабораторные работы по Агрегатам.docx
#
27.03.20151.02 Mб198Лабораторные работы по ПЭЭ.doc
#
01.07.202567.14 Кб0ЛабРабота_1_2_3_4.docx
#
27.03.2015643.48 Кб28лабСЭС.pdf