Нейман часть 3

УДК 621.3.011.71(075.8) Н 46

Рецензенты:

д-р техн. наук, проф. А.В. Сапсалев, канд. техн. наук, доц. Ю.В. Петренко

Работа подготовлена на кафедре теоретических основ электротехники для студентов дневного и заочного отделений

электротехнических специальностей

Нейман В.Ю.

Н 46 Теоретические основы электротехники в примерах и задачах. Ч. 3. Четырехполюсники и трехфазные цепи: учеб. пособие / В.Ю. Нейман. – Новосибирск: Изд-во НГТУ, 2010. – 144 с.

ISBN 978-5-7782-1547-4

В пособии на значительном числе примеров решения типовых задач рассматриваются методы расчета четырехполюсников и трехфазных цепей. Предлагаются аналогичные задачи для самостоятельного решения с ответами.

Показаны приемы использования персонального компьютера для автоматизации расчетов электрических цепей.

Структура и содержание пособия соответствуют программе курса «Теоретические основы электротехники» для электротехнических специальностей вузов.

Предназначено для самостоятельной работы студентов, а также может быть полезно преподавателям при организации учебного процесса.

УДК 621.3.011.71(075.8)

2

3

ВВЕДЕНИЕ

Цель пособия – оказать помощь студентам, изучающим курс «Теоретические основы электротехники», в их самостоятельной работе.

Усвоение материала из разделов курса «Четырехполюсники» и «Трехфазные цепи» становится возможным только с приобретением практических навыков, получаемых в процессе решения задач.

Так же как и первые две части пособия, третья состоит из отдельных разделов, разбитых по темам в соответствии с программой курса. Часть задач рассмотрена с их решением. В задачах, приведенных для самостоятельного решения, даны только ответы.

По каждой из задач изложен подробный алгоритм расчета, который поясняется на примере четырех и более задач с их решениями.

Приведенные примеры расчета электрических цепей соответствуют типовым задачам, которые могут оказаться полезными при подготовке к практическим занятиям и выполнении домашних заданий, а также при подготовке к экзаменам, обладают требуемой сложностью и трудоемкостью.

В качестве помощи студентам в изучении дисциплины рассмотрены приемы работы на компьютере с целью автоматизации расчетов электрических цепей в среде MathCAD. Предполагается, что учащийся имеет начальное представление о математическом пакете MathCAD из пройденного курса информатики. Это позволяет переложить выполнение рутинных математических расчетов на компьютер.

4

1.ОСНОВЫ РАСЧЕТА ЧЕТЫРЕХПОЛЮСНИКОВ

Соотношения между напряжениями и токами на входе и выходе четырехполюсника связаны между собой основными уравнениями. Это позволяет, не производя расчетов токов и напряжений внутри заданной схемы, получить аналитическую зависимость между токами и напряжениями на входе и выходе четырехполюсника.

Расчет пассивных четырехполюсников сводится к определению коэффициентов, связывающих его уравнения, характеристических параметров и передаточных свойств четырехполюсников.

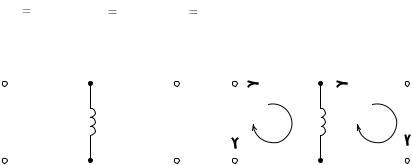
Задача 1.1

Определить коэффициенты четырехполюсника (рис. 1.1) для уравнений, составленных по А -форме, записать матрицу А -параметров

Решение

1. Решение получим приведением уравнений, составленных по методу контурных токов, к виду основных уравнений четырехполюсника, записанных в А-форме:

Положительные направления напряжений, токов и обходов контуров зададим в соответствии с расчетной схемой, приведенной на рис. 1.2.

2. По методу контурных токов для схемы (рис. 1.2) получим систему уравнений

Из второго уравнения системы выразим ток I1 и подставим в пер-

вое уравнение. После некоторых преобразований системы приведем ее к уравнениям четырехполюсника А-формы:

6

3. Из сравнения полученной системы уравнений с основными уравнениями четырехполюсника, записанными в A-форме при заданных числовых значениях, находим А-параметры:

Уравнение связи коэффициентов выполняется.

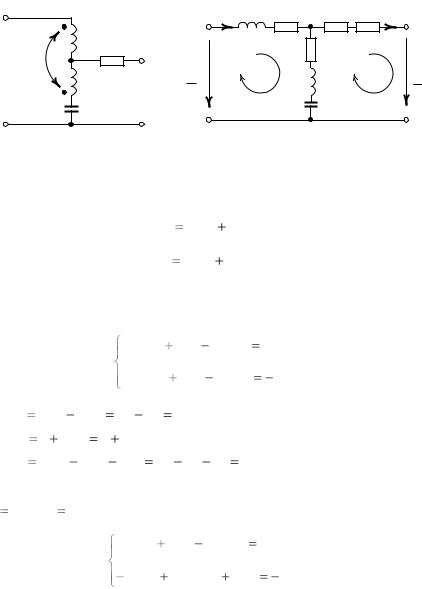
Задача 1.2

Определить коэффициенты уравнений А-формы и записать систему уравнений несимметричного Т-образного четырехполюсника (рис. 1.3) в матричной форме. Найти характеристические сопротивления и постоянную передачи четырехполюсника, если r 4 Ом ,

xL1 6 Ом , xL2 7 Ом , xM 2 Ом , xС 3 Ом .

Решение

1. Решение получим для схемы с развязкой индуктивных связей (рис. 1.4) приведением уравнений, составленных по методу контурных

7

токов, к виду основных уравнений четырехполюсника, записанных в А-форме:

2. С учетом заданных положительных направлений контурных токов I11 , I 22 для расчетной схемы (рис. 1.4) получим

Выразим ток I1 из второго уравнения системы и подставим в пер-

вое уравнение. После приведения системы к уравнениям четырехполюсника А-формы окончательно получаем

3. Из сравнения полученных уравнений четырехполюсника по рис. 1.4 с основными уравнениями, записанными в А-форме для коэффициентов, получим

4. Система уравнений четырехполюсника в матричной форме

5. Характеристическое (входное) сопротивление со стороны первичных выводов 1 и 1I четырехполюсника (рис. 1.3):

33,23 174,8о 5,76 87,4о Ом .

Характеристическое (входное) сопротивление со стороны вторичных выводов 2 и 2I четырехполюсника (рис. 1.3):

Задача 1.3

Для схемы (рис. 1.5) по значениям напряжений и токов в режимах холостого хода и короткого замыкания определить коэффициенты четырехполюсника и записать матрицу A -параметров, если r 15 Ом ,

xL 10 Ом , xС 5 Ом .

10