
сборник задач по дискретке другой вариант
.pdfРояк С.Х., Рояк М.Э.
Дискретная
математика
Сборник задач
1
1.СИСТЕМЫ СЧИСЛЕНИЯ
1.Записать в десятичной системе счисления числа, записанные в современной Римской системе: IV, VIII, XIX, XL, MCMLXXXIX, XCIV, CMMLXXXIX.
2.Записать в современной Римской системе счисления числа: 24, 46, 98, 176, 1963, 1998.
3.Записать в d-ичной системе числа d 2 , d 3 , …
4.В турнире участвовали 13 мальчиков и 54 девочки, а всего 100 человек. В какой системе счисления сделаны эти записи?
5.В какой системе счисления
2·2=10, 4·4=31, 3·3=10?
6.Как изменится число 325006 если а) приписать справа один нуль; б) приписать справа три нуля; в) отбросить справа два нуля?
7.В какой системе счисления верно:
а) 212d=2310, б) 53d=3310
8. Какое из чисел больше: |
|
|
|
|
|
|
|
|
||||||||||
а) 310 или 38, |
|
|
|
б) 1410 или 148, |
|
|
|
|
|
|
||||||||
в) æ |
1 |
ö |
или |
æ |
1 |
ö |
, |
г) æ |
1 |
ö |
или æ |
1 |
ö |
, |
д) 0,11 |
|
или 0,11 |
? |
|
÷ |
ç |
|
÷ |
|
÷ |
|
÷ |
2 |
|||||||||
ç |
|
|
|
|
ç |
|
ç |
|
|
|
|
10 |
||||||
è |
3 ø5 |
|
è |
3 ø8 |
|
è14 |
ø5 |
è14 |
ø8 |
|
|
|
|
|
||||
9.Какое самое большое 5-значное число в 3-ичной, 8-ричной системах?
10.Записать в десятичной системе счисления числа:
1324, 10023, 7778, 31758, 21214, 55417.
11. Записать числа 49, 57, 101, 196 а) в 3-ичной системе счисления; б) в 5-ричной системе счисления; в) в 7-ричной системе счисления.
2
12. Заполнить таблицу: первый столбец – числа от 0 до 15, второй столбец – соответствующие двоичные числа, третий столбец – соответствующие 16-ичные числа, четвертый столбец – соответствующие 4-ичные числа.
13.Перевести числа
1100010112, 10101001002, 1100000102, 100110012.
а) в 4-ичную систему счисления; б) в 8-ричную систему счисления; в) в 16-ричную систему счисления.
14. Перевести числа 5218, 6158, 4038, 1258 в 2-ичную систему счисления.
15.Перевести числа A3516, D2716, F4916, E8B516, С60116
а) в 4-ичную систему счисления; б) в 2-ричную систему счисления; в) в 8-ричную систему счисления.
16.Сколько существует
a)5-значных чисел в d-ичной системе счисления;
b)n-значных чисел в d-ичной системе счисления?
17.*Доказать V и VI алгоритмы.
18.Вычислить:
1)101.11012 +11.10112 ,
2)11101.112 +10011.12 ,
3)101101.0112 +1111.1012 ,
4)11.12 ×10.12 ,
5)1001.112 ×1.112 ,
6)0.10112 ×1.12 .
3

2.ТЕОРИЯ МНОЖЕСТВ
1.Задать множества перечислением их элементов и найти B IC ,
A U B , ( A U B) IC , A I B IC , если:
1)A – множество делителей числа 12; B = {1;5} ; C – множество
нечетных чисел x таких, что 2 < x < 13; |
x |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
2) A – множество четных чисел |
таких, что 3 < x < 10; B – |
|||||||||||||||||||||
множество |
|
делителей |
числа 21; |
C – |
множество |
простых |
|
чисел, |
|||||||||||||||
меньших 12. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2. Изобразить на координатной прямой множества A U |
|
, |
|
|
I B |
|||||||||||||||||
B |
A |
||||||||||||||||||||||
и |
|
, если: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
A I B |
] |
|
[ |
|
) |
|
|
|
( |
] |
( |
|
|
) |
|
|
|
|
|||||
|
1) A = |
( |
−1,0 |
и B = |
0,2 |
|
2) A |
= |
−∞,−3 |
|
|
|
|
||||||||||
|
|
|
|
|
, |
|
−∞,1 и B = |
|
|
|
, |
|
|
|
|||||||||
3) A = {x x Î ¡ и - 5 £ x < 2} и B = {x x Ρ и 1 < x £ 4},
4) A = {x x Î ¡ и x < 5} и B = {x x Î ¡ и x ³ -7}.
3. Дать геометрическую интерпретацию множества A I B \ C , если
A = {(x, y) x, y Ρ и x £ 4, y £ 4};
B= {(x, y) x, y Î ¡ и x2 + y2 £ 25};
C= {(x, y) x, y Î ¡ и y > 0}.
4.Определить множества:
1){x x = 5y, y ΢} \ {x x =10y, y ΢};
2){x x = 4n + 2,nÎ ¥}I{x x = 3n,nÎ ¥};
3){x x = 2y, y ΢}I{x x = 3y, y ΢};
4){x x = 2y, y ΢}U{x x = 3y, y ΢}.
5.Доказать, что:
1) A A; |
3) A I B A A U B ; |
||
4) A I B B |
A U B ; |
||
2) если A B и B C , то A C ; |
|||
5) A \ B A . |
|
||
|
|
||
4 |
|
|
|
6. Какой знак из множества {=, ¹, É, Ì} можно поставить вместо символа «?», чтобы полученное утверждение было верным.
1) |
{1,3} ? {1,2,3} , |
|
|
|
5) |
{( |
|
) |
|
( |
3,2 |
)} |
? |
{( |
|
) |
, |
( |
2,3 |
)} |
, |
|
||||||
|
|
|
|
2,1 , |
|
|
1,2 |
|
|
|
|
|||||||||||||||||
2) |
{2,3,4} ? {1,2,3} , |
|
|
6) |
{{ } |
, |
{ |
}} |
? |
{( |
|
) |
|
( |
2,3 |
)} |
, |
|
||||||||||
3) |
|
|
? x |
|
x делитель 6 , |
1,2 |
|
|
|
2,3 |
|
2,1 , |
|
|
|
|||||||||||||
1,2,3 |
|
|
{{ } |
|
{ }} |
|
{{ } |
|
{ } { }} |
|
||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
{ |
} |
{ |
|
|
|
|
|
} |
7) |
, |
? |
|
, |
||||||||||||||
|
|
|
|
|
|
1,2 |
|
|
|
2,3 |
|
2,1 , |
|
3,2 , |
1,3 |
|||||||||||||
4) |
{{ } |
{ }} |
? |
{ |
} |
, |
8) ? |
{ } . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1,2 |
, |
2,3 |
|
|
1,2,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
7.Какие из утверждений верны для всех A , B и C ?
1)Если AÎ B и B ÎC , то AÎC ,
2)Если A Ì B и B ÎC , то AÎC ,
3)Если A I B C и A UC B , то A IC = ,
4)Если A ¹ B и B ¹ C , то A ¹ C ,
5)Если A (B UC) и B (A UC), то B = Æ .
8. Даны |
два |
произвольных |
множества |
A |
и |
B |
такие, |
что |
||
A I B = Æ. Определить множества A \ B и B \ A. |
|
|
|
|
|
|||||
9. Даны |
два |
произвольных |
множества |
A |
и |
B |
такие, |
что |
||
A I |
|
= Æ. Определить множества A I B и A U B . |
|
|
|
|
||||
B |
|
|
|
|
||||||
10.Дано произвольное множество A . Найти множества
A I A, A U A, A \ A.
11.Существуют ли такие множества A , B и C , что
A I B ¹ Æ , A IC = Æ , (AI B) \ C = Æ?
12. Доказать, что:
A B A U B = B A I B = A A \ B = A U B = U.
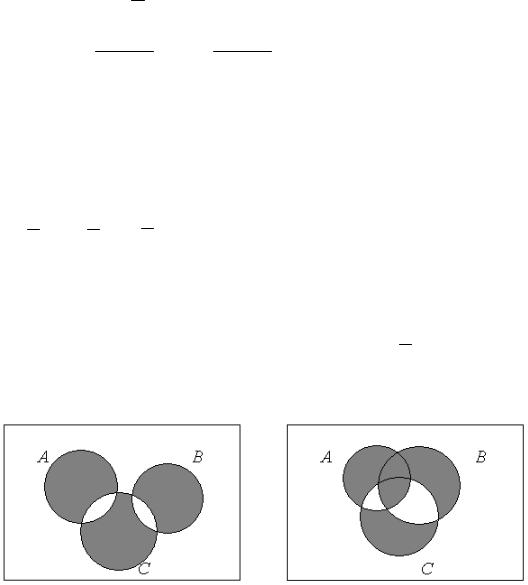
13. Опишите множества, соответствующие закрашенной части
диаграммы Венна: |
|
1) |
2) |
5
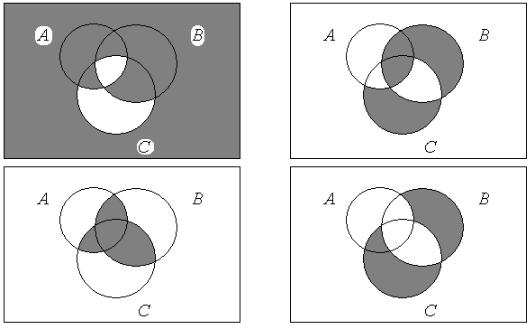
3) |
4) |
5) |
6) |
14. Доказать, что
1) |
A \ (B UC) = ( A \ B) I( A \ C) , |
16) |
A U B Ì C Û A Ì C и B Ì C , |
||||||||||||||||
2) |
A \ (B IC) = ( A \ B) U( A \ C) , |
17) |
A Ì B IC Û A Ì B и A Ì C , |
||||||||||||||||
3) |
A \ ( A \ B) = A I B , |
18) |
A B UC A I |
B |
|
C , |
|||||||||||||
19) |
A Ì B Þ C \ B Ì C \ A, |
||||||||||||||||||
4) |
A \ B = A \ ( A I B), |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
20) |
A Ì B Þ B Ì A, |
||||||||||||||||||
5) |
A I(B \ C) = ( A I B) \ ( A IC) , |
||||||||||||||||||
21) |
A U B = A I B Þ A = B , |
||||||||||||||||||
6) |
( A I B) \ ( A IC) = ( A I B) \ C , |
22) |
A= |
|
Û AIB =Æ и AUB =U , |
||||||||||||||
B |
|||||||||||||||||||
7) |
A I(B \ C) = ( A I B) \ C , |
23) |
A ¸ (B ¸ C) = (A ¸ B) ¸ C , |
||||||||||||||||
8) |
( A \ B) \ C = ( A \ C) \ (B \ C), |
24) |
A ¸ ( A ¸ B) = B , |
||||||||||||||||
9) |
A U B = A U(B \ A) , |
25) |
A U B = A ¸ B ¸ ( A I B), |
||||||||||||||||
10) ( A I B) U(A I |
|
|
) = A, |
26) |
A U B = (A ¸ B) U( A I B), |
||||||||||||||
B |
|||||||||||||||||||
11) ( A U B) I(A U |
|
) = A, |
27) |
A \ B = A ¸ ( A I B), |
|||||||||||||||
B |
|||||||||||||||||||
12) ( |
|
U B)I A = A I B , |
28) |
A ¸ B = Æ Û A = B , |
|||||||||||||||
A |
29) |
A I B = Æ Þ A U B = A ¸ B , |
|||||||||||||||||
13) ( A U B) \ C = (A \ C) U(B \ C), |
30) |
AI B C A |
|
UC , |
|||||||||||||||
B |
|||||||||||||||||||
14) |
A \ (B \ C) = (A \ B) U(A IC), |
31) |
AU(BIC) = (AUB) I(AUC), |
||||||||||||||||
15) |
A \ (B UC) = (A \ B) \ C , |
32) (A U B) I A = (A I B)U A = A , |
|||||||||||||||||
|
|
|
|
|
|
|
33) |
A I(B \ A) = Æ, |
|||||||||||
34) ( A I B) U(C I D) = (A UC) I(B UC) I( A U D) I(B U D).
6

15. Доказать следующие тождества: |
|
|
|
|
||||||
1) UUAkt =UU Akt |
, |
5) |
U(B I Ak |
æ |
ö |
, |
||||
k K t T |
t T k K |
|
) = B Iç UAk ÷ |
|||||||
2) IIAkt = II Akt |
, |
|
k K |
è k K |
ø |
|
||||
|
|
æ |
ö |
|
||||||
k K t T |
t T k K |
|
6) |
I(B U Ak |
) = B Uç IAk ÷, |
|||||
|
|
|
|
|
|
|||||
3) U Ak = I Ak , |
|
|||||||||
|
7) |
k K |
è k K |
ø |
|
|||||
k K |
k K |
|
U Ak U UBk = U(Ak U Bk ), |
|||||||
|
|
|
|
|
|
|||||
4) |
|
= U |
|
, |
|
|
|
|
|
|
I Ak |
|
|
|
|
|
|
||||
Ak |
|
|
k K k K |
k K |
|
|
||||
k K |
k K |
|
8) |
UIAkt IU Akt . |
|
|
||||
|
|
|
|
|
|
|
k K t T |
t T k K |
|
|
16.Доказать, что:
1)UAi есть наименьшее множество, содержащее все множества Ai ;
i I
2) IAi есть наибольшее множество, содержащееся во всех мно-
i I
жествах Ai .
17.Найти булеаны множеств {x}, {1,2}, {1,2,3} , , {Æ} , { ,{ }}.
18.Доказать, что:
1)P( AI B) = P(A)IP(B),
2) P(A U B) = {A1 U B1 A1 P(A) и B1 P(B)},
3) |
æ |
ö |
= IP(Ai ), |
|
|
|
|||
PçIAi ÷ |
|
|
|
||||||
|
è i I |
ø |
|
i I |
|
|
|
|
|
4) |
æ |
ö |
= |
ì |
|
Bi ÎP(Ai |
ü |
||
|
|||||||||
PçUAi ÷ |
íUBi |
|
)ý. |
||||||
|
è i I |
ø |
{ |
îi I |
|
|
{ |
} |
þ |
|
|
|
} |
, B = |
|
||||
19. Пусть A = 1,2,3 |
|
a,b . Определить множества |
|||||||
1) |
A× B , 2) B × A , 3) A× A , 4) B × B , 5) A× , 6) × B . |
||||||||
20. Пусть A – множество точек отрезка [0,1]; B – множество точек отрезка [2,3]; C = {4,5,6}; D – множество точек квадрата с вершинами в точках (0,0), (0,1), (1,0), (1,1). Найти геометрическую интерпрета-
цию множеств: |
|
|
1) A× B , |
3) C × B , |
5) C × D , |
2) A× C , |
4) A× D , |
6) D × B . |
7

21. |
Доказать, что существуют A , |
B и C такие, что: |
||
1) |
A´ B ¹ B ´ A , |
3) |
A´(B´C) = ( A´ B)´C , |
|
2) |
A´ B = B ´ A, |
4) |
A´(B ´C) ¹ ( A´ B)´C . |
|
22. |
Доказать, что |
( A´ B) U(C ´ D) Ì ( AUC)´(B U D). При каких |
||
A , B , C , D включение можно заменить равенством?
23.Доказать, что для произвольных множеств A , B , C , D
1)( A U B)´C = ( A´C) U(B ´C) ,
2)( A \ B)´C = ( A´C) \ (B ´C),
3)A´(B \ C) = ( A´ B) \ ( A´C),
4)( A I B)´(C I D) = ( A´C) I(B ´ D) ,
5)A´ B = ( A´ D) I(C ´ B), где A Ì C и B D.
24.Пусть A ¹ Æ, B ¹ Æ и ( A´ B) U(B´ A) = C ´ D. Доказать, что в этом случае A = B = C = D .
25.Задать отношение P перечислением его элементов или матрицей отношения, если P Ì A2 , A = {1,2,3,4,5,6,7,8,9}
1)P = {(x, y) (x +1) делитель (x + y)};
2)P = {(x, y) x ¹ 1 и x делитель (x + y)}.
26. Задать отношение P Ì A2 , |
{ |
} |
перечислением |
его |
||||||||||
A = 1,3,5,7 |
||||||||||||||
элементов и определить |
|
и P−1 , если |
|
|
|
|
|
|
|
|
|
|||
P |
|
|
|
|
|
|
|
|
|
|||||
1) P = {(x, y) |
|
x + 2 = y}; |
3) P = {(x, y) |
|
|
|
x + y -1Î A}; |
|
||||||
|
|
|
|
|||||||||||
2) P = {(x, y) |
|
(x + y)/ 2Î A}; |
4) P = {(x, y) |
|
|
2y + x Î A}. |
|
|||||||
|
|
|
||||||||||||
27. Составить |
|
матрицы отношений |
P , |
|
|
и P−1 , |
если |
|||||||
|
|
P |
||||||||||||
P Ì (P(A))2 , A = {a,b,c}.
1) P = {(X ,Y ) |
|
|
X Ì Y, X ¹ Y}; |
3) P = {(X ,Y ) |
|
X IY ¹ Æ}; |
||
|
|
|||||||
2) P = {(X ,Y ) |
|
|
X Ì Y}; |
4) P = {(X ,Y ) |
|
X = |
|
}. |
|
|
|
Y |
|||||
8

28. Определить отношения:
1) P o S , 2) S oT , 3) S−1 o S 4) S o S −1 , 5) (P oS )−1 , 6) S −1 o P−1 , 7) P−1 o S −1 , 8) (P oS ) oT , 9) P o(S oT ),
если T = {(11, ),(10,W),(13,*),(12,W),(13,d)} ,
P= {(1,7),(4,6),(5,6),(2,8)} , S = {(6,10),(6,11),(7,10),(8,13)}.
29.Найти P oS, (P oS )−1 , если:
1) X – множество точек плоскости, Y – множество окружностей, Z – множество треугольников?
P = {(x, y) |
|
x X , y Y и x центр окружности y}; |
||
|
||||
S = {(x, y) |
|
|
|
x Y, y Z и окружность x вписана в треугольник y} , |
|
|
|||
2) X – множество преподавателей института, Y – множество читаемых дисциплин, Z – множество академических групп,
P ={(x, y) x X , y Y и преподаватель x ведет занятия по дисциплине y};
S ={(x, y) x Y, y Z и студенты группы y изучают дисциплину x}, 3) X – множество мужчин, Y – множество людей, Z – множе-
ство женщин, P = {(x, y) x X , y Y и x отец y},
S= {(x, y) x Y, y Z и x родитель y}.
30.Пусть отношения P и S определены на множестве людей следующим образом: P = {(x, y) x дочь y}, S = {(x, y) x отец y}. Опре-
делить следующие отношения:
1) P2 , 2) S 2 , 3) P o S 4) S o P , 5) S−1 o S −1 , 6) P−1 o P−1 , 7) S o P−1 , 8) P−1 o S , 9) P−1 o S −1 , 10) S −1 o P .
31. Пусть |
P = {(x, y) |
|
x, y ¡ и y = x4 +1}, |
S = {(x, y) |
|
x, y ¡ и y =7x3}. |
|
|
|||||
Определить отношения P o S , S o P , P−1 , |
S −1 . Найти образ и прообраз |
|||||
множества [2,10) относительно отношений P и S . |
|
|
||||
32. Пусть |
P = {(x, y) |
|
x, y ¡ и y > x4 +1}, |
S = {(x, y) |
|
x, y ¡ и y ≤7x3}. |
|
|
|||||
Найти P( X ), P−1 ( X ), |
|
S ( X ), S−1 (X ), где X = (2,10]. |
||||
9

33. Пусть P = {(x, y) x, y ¥ и x делит y}. Найти δP , ρP , P−1 ,
P−1 o P , P o P−1 , P oP , P( A), P−1 (B), если
1) |
A = {x |
|
|
x ¥ и x ≤ 7}, B = {x |
|
x ¥ и 5 ≤ x ≤10}; |
|||
|
|
|
|||||||
2) |
A = {x |
|
x ¥ и 1 < x ≤ 7}, B = {x |
|
x ¥ и x кратно 5}. |
||||
|
|
||||||||
34. Найти
P−1 ((2,10])
1)P = {(x, y
2)P = {(x, y
3)P = {(x, y
4)P = {(x, y
5)P = {(x, y
6)P = {(x, y
7)P = {(x, y
8)P = {(x, y
9)P = {(x, y
10)P = {(x,
11)P = {(x,
12)P = {(x,
|
|
|
|
δP , ρP , P−1 , |
P−1oP , |
P o P−1 , |
|
|||||
для отношений: |
|
|
|
|
|
|||||||
) |
|
|
|
x, y Ρ и x + y £ |
0}, |
13) |
P = {(x, y) |
|
||||
|
|
|
||||||||||
) |
|
|
|
x, y Ρ и x + y > 0}, |
14) |
P = {(x, y) |
|
|
||||
|
|
|
|
|||||||||
) |
|
|
|
x, y Ρ и x + y ³ 2}, |
15) |
P = {(x, y) |
|
|||||
|
|
|
||||||||||
) |
|
|
|
x, y Ρ и x + y < 7}, |
16) |
P = {(x, y) |
|
|||||
|
|
|
||||||||||
) |
|
|
|
x, y Ρ и x - y < 0}, |
17) |
P = {(x, y) |
|
|
||||
|
|
|
|
|||||||||
) |
|
|
|
x, y Ρ и x - y ³ 0}, |
18) |
P = {(x, y) |
|
|
||||
|
|
|
|
|||||||||
) |
|
x, y Ρ и x - y £ 9}, |
19) |
P = {(x, y) |
|
|||||||
|
|
|||||||||||
) |
|
x, y Ρ и x - y > 3}, |
20) |
P = {(x, y) |
|
|||||||
|
|
|||||||||||
) |
|
x, y Ρ и xy < -5}, |
21) |
P = {(x, y) |
|
|||||||
|
|
|||||||||||
y) |
|
|
x, y Ρ и xy > -5}, |
22) |
P = {(x, y) |
|
||||||
|
|
|||||||||||
y) |
|
|
x, y Ρ и xy < 20}, |
23) |
P = {(x, y) |
|
|
|||||
|
|
|
|
|||||||||
y) |
|
|
x, y Ρ и xy > 20}, |
24) |
P = {(x, y) |
|
||||||
|
|
|
||||||||||
P oP , P ([−5,−1)),
x, y Ρ и 3x - 5y < 0}, x, y Ρ и 7x - 4y ³ 0}, x, y Ρ и 2x - 3y > 5}, x, y Ρ и 9x - 5y £ 2}, x, y Ρ и 2x + 5y ³ 0}, x, y Ρ и 7x + 3y < 2}, x, y Ρ и x2 - y < 0}, x, y Ρ и x2 - y > 0}, x, y Ρ и x2 + y < 0}, x, y Ρ и x2 + y > 0}, x, y Ρ и x3 > y2},
x, y Ρ и x2 > y + 2}.
35. Найти δP , |
ρP , P−1 , P−1 o P , P o P−1 , P oP , P( A), P−1 (B), если |
|||||||||||||||||||||
1) |
P = {(x, y) |
|
x, y Ρ+ и ln x < y}, A = B = (1,3]; |
|
|
|||||||||||||||||
|
|
|
||||||||||||||||||||
2) |
P = {(x, y) |
|
|
|
x, y Ρ и ex > y}, |
A = B = (1,3]; |
|
|
||||||||||||||
|
|
|
|
|
||||||||||||||||||
|
|
{( |
|
) |
|
|
|
} |
|
( |
|
] |
|
[ |
) |
|
||||||
3) |
P = |
|
x, y |
|
|
|
|
|
|
x, y Ρ и |
|
x |
|
< y , |
A = |
|
−2,5 |
|
, |
B = 1,7 |
|
; |
4) |
P = {(x, y) |
|
|
x, y Ρ и |
|
x |
|
> y}, |
A = (−3,7 |
], |
B = [2,9); |
|||||||||||
|
|
|
|
|||||||||||||||||||
5) P = {(x, y) |
|
|
|
x, y Î[-p/ 2,p/ 2] и sin x £ y}, |
A = B = (0,π / 2]. |
|||||||||||||||||
|
|
|||||||||||||||||||||
10
