
Конспект по ТАУ
.pdf
№ 35 Создание комбинированных САУ
Основным методом, используемым при создании инвариантных систем, является применение комбинированного управления, при котором управляющее воздействие реализуется не только по отклонению регулируемой величины, но и по возмущению, для этого измеряется основное возмущающее воздействием и сигнал через корректирующее звено вводится в САУ.
При этом реализуется принцип двухканальности и не возникает противоречия между устойчивостью и инвариантностью, как это имеет место в одноконтурных системах, реализующих условие инвариантности за счет повышения коэффициента усиления системы.
Условия реализации абсолютной инвариантности легко проследить на примерах (рисунок 8.4,8.5). Для системы (рисунок 8.4)
Wз p |
xвых p |
|
Wk p 1 |
. W p 1. |
||
xвх p |
1 W p |
|
||||
|
|
|
||||
Отсюда |
|
|
k |
|
|
|
|
|
k |
|
|
1 |
|
|
|
W |
p |
1 W p , или |
W |
p |
|
|
. |
||||
W p 1 |
W p |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для системы (8.5): |
|
|
1 Wk p Wp p W0 p |
|
|
|
|||||||
Wз p |
xвых p |
|
0, |
|
|||||||||
|
p |
1 W0 p Wp p |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||
или Wk p Wp p 1, Wk p |
|
1 |
. |
|
|
|
|
||||||
|
|
|
|
|
|
||||||||
Wp p |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
(8.5)
(8.6)
Введение дополнительных воздействий не изменяет характеристического уравнения замкнутой САУ, поскольку корректирующие звенья не входят в замкнутый контур прохождения сигнала. При этом не будет нарушаться не только устойчивость САУ, но и сохраняться оценки качества переходного процесса, базирующиеся на использовании корней характеристического уравнения.
Поскольку для физической реализации передаточной функции |
W p |
|
|
|
|
n m , то при реализации условия абсолютной инвариантности |
W |
|
|
|
|
|
|
k |
|
b |
0 |
p |
m |
b p |
m 1 |
b |
m |
необходимо, чтобы |
|||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
n |
a p |
n 1 |
a |
|
|
|
|||
|
|
a |
0 |
p |
n |
|
|
|||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||
p |
|
|
1 |
сталкиваются с затруднениями |
||||||||||
W |
p |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
реализации производных. Например, если
W p |
K |
p |
T p K |
p |
|
|
|
p |
|
T p |
|
Это звено физически реализуемо, |
|||||||||
|
n |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
, то |
W |
|
n |
|
. |
||||||||||
|
|
|
|
|
|
|
T p 1 |
|
|
|
|
|
|
|
|||||||
p |
|
|
T p |
|
|
|
k |
K |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
||
дифференцирующее звено. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
При |
|
W |
p |
p |
|
K |
, |
необходимо, |
чтобы W |
p |
p |
|
p |
2 |
. |
||||||
|
|
|
|
|
p Tp 1 |
|
|
|
|
|
|
k |
1 |
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
m
n
1. Это реальное
Если регулятор обладает астатизмом |
n -го порядка, то W |
p должно реализовать производную |
n -го и |
||
|
|
n 1 |
k |
|
|
выше порядков и не иметь производных до |
порядка, что физически невозможно реализовать. |
|
|||
В этом случае реализуется частичная инвариантность за счет замены идеальных дифференцирующих звеньев реальными.
|
|
Wн(p) |
|
|
+ |
xвх |
- |
W(p) |
x |
||
|
|
вых |
Рисунок 8.4 - Реализация инвариантности по заданию САУ
|
|
|
|
|
|
|
|
|
|
|
W (p) |
|
|
|
|
|
|
|
к |
|
|
|
|
x |
вх |
+ |
W (p) |
- |
W (p) |
x |
вых |
|
|
|
|
||||
|
|
- |
|
|
|
||
|
|
р |
|
о |
|
|
|
|
|
|
|
|
|
Рисунок 8.5 - Реализация инвариантности по возмущению САУ
Можно реализовать инвариантность по нескольким возмущениям, но это практически сложно. Для САУ, описываемых дифференциальными уравнениями 1-го и 2-го порядка, когда необходимое
условие устойчивости (положительность коэффициентов характеристического уравнения) является и
достаточным, можно корректирующие звенья не устанавливать, а увеличивать коэффициент усиления |
||||
разомкнутой САУ. При этом (рисунок 8.4): |
||||
W p |
xвых p |
|
W p |
. |
|
|
|||
з |
xвх p |
|
1 W p |
|
|
|
|
||
Коэффициент усиления разомкнутой САУ равен
K lim W p p 0
W 0
. Для того, чтобы САУ была
инвариантна к задающему воздействию, необходимо, чтобы
|
|
|
|
|
x |
вых |
p |
|
|
W 0 |
|
|
K |
|
|||
W |
|
p |
|
|
|
|
|
|
|
|
|
1. Это отношение будет стремиться к единице при |
|||||
з |
|
|
|
|
x |
вх |
p |
|
|
|
|
|
K 1 |
|
|||
|
|
|
|
|
|
|
|
1 W 0 |
|
|
|||||||
|
|
W 0 |
. При
этом САУ будет инвариантна и к возмущающему воздействию (рисунок 8.5).
W |
p |
з |
|
Если
|
xвых p |
|
W |
|
|
||
|
|
|
0 p |
|
. |
||
p |
W |
p W |
p |
||||
|
1 |
|
|||||
|
|
|
0 |
p |
|
|
|
p |
|
p |
K |
p |
, |
|
з |
0. |
W p |
W 0 |
|
то |
W p |
||||
p 0 |
|
|
|
|
|
|
|
|
36. Инвариантность по задающему воздействию
В настоящее время существует три направления создания инвариантных САУ:
1.Системы с одной регулируемой величиной, работающие по отклонению. В таких системах условие абсолютной инвариантности достигается при коэффициенте усиления разомкнутой САУ равном бесконечности.
2.Создание комбинированных систем.
3.Использование принципа двухканальности Б.Н. Петрова в многосвязных системах.
САУ называется инвариантной по отношению к задающему воздействию, если после завершения переходного процесса, определяемого начальными условиями, ее ошибка не зависит от этого воздействия.
САУ инвариантна к задающему воздействию, если ее передаточная функция по отношению к нему равна единице
W(p)=1.
37. Инвариантность по возмущающему воздействию
САУ называется инвариантной по отношению к возмущающему воздействию, если после завершения переходного процесса, определяемого начальными условиями, регулируемая величина и ошибка системы не зависят от этого воздействия.
САУ инвариантна к возмущающему воздействию, если ее передаточная функция по отношению к нему равна нулю W(p)=0.
Возмущающее воздействие – это такое воздействие, которое стремится нарушить требуемую функциональную связь между переменными, характеризующими ее состояние.
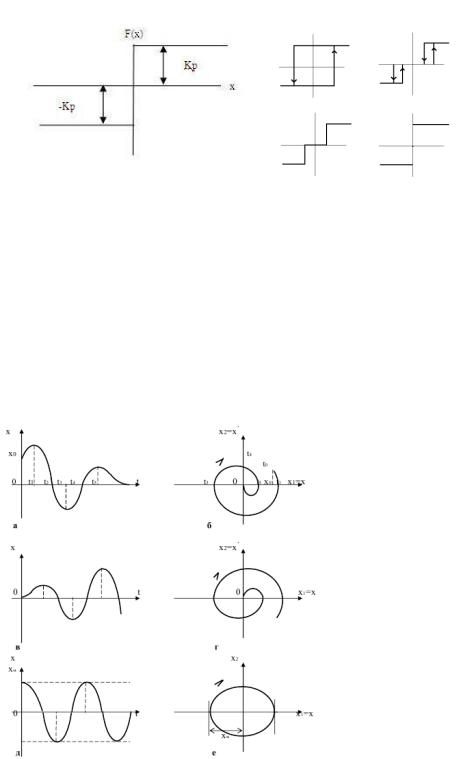
38. Основные типы нелинейностей
Нелинейной системой автоматического управления называется такая система, которая содержит хотя бы одно звено, описываемое нелинейным уравнением.
Нелинейности бывают:
релейного типа
динамические (описываются нелинейными дифференциальными зависимостями);
переменной структуры (эта нелинейность связана с изменением значения переменной х, например: система, состоящая из линейных звеньев, создает нелинейное устройство, реализующее определенную функцию переключения Ф (фи))
логического типа (элемент, имеющий несколько входов выдает ступенчатый сигнал. В зависимости от определенных логических комбинаций входных величин.)
релейные автоматические системы
39.Нелинейности релейного типа.
Характеристика релейного элемента без среднего положения (2х-розиционный).
40. Релейные автоматические системы.
Это наиболее простой класс нелинейных систем, т.к. благодаря специфике релейного элемента, создающего воздействие на релейную часть системы в виде прямоугольных импульсов одинаковой высоты. Исследования сводятся к исследованию линейной части, подверженной этим импульсам.
Управляющее воздействие приложенное к линейной части системы можно представить в виде суммы воздействий простейшего вида, а реакцию линейной части найти по принципу суперпозиции на сумму реакций на каждое из них.
41. Построение переходных процессов в релейных системах.
Главная особенность релейных систем что они не подчиняются принципу наложения, а форма и показатели переходного процесса зависят от величины и формы внешнего воздействия.
42. Устойчивость нелинейных систем.
Самые важные для анализа нелинейных систем свойства фазовых траекторий заключаются в следующем:
Неустойчивому процессу соответствует фазовая траектория, удаляющаяся от начала координат.
Периодическому процессу соответствует замкнутая фазовая траектория, называемая предельным циклом.
Устойчивость нелинейной системы оценивают по 3 признакам:
–устойчивость в малом – это устойчивость системы при бесконечно малых отклонениях от исходного режима. При чуть больших отклонениях система становится неустойчивой.
–система устойчива в большом, если система устойчива при бесконечно больших отклонениях, которые возможны в данной системе. При малых система может быть неустойчива.
–система устойчива в целом, если система устойчива при любых воздействиях.
43.Устойчивость релейных систем.
Релейная автоматическая система устойчива, если для всякого заданного числа Е>0 можно найти такое число N(E)>0 что для всех изчезающих воздействий f(t), таких что  , входная величина релейного элемента x(t) удовлетворит неравенству
, входная величина релейного элемента x(t) удовлетворит неравенству 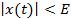 для всех t>t0.
для всех t>t0.
Если релейная автоматическая система устойчива лишь при достаточно малых значениях, то имеет место устойчивость в малом. Если же релейная система устойчива при любых конечных значениях, то имеет место устойчивость в большом. Если релейная система устойчива при любых N, то имеет место устойчивость в целом.
44. Вынужденные колебания в релейных системах.
Внешнее периодическое воздействие навязывает системе свою частоту и подавляет автоколебания, возможные в системе. В этом случае система автоматически синхронизируется частотой внешнего воздействия. В ней имеет место вынужденные колебания, частота которых равна частоте внешнего воздействия.
45. Линеаризация релейных систем.
Подача на вход релейного элемента дополнительного высокочастотного периодического воздействия наряду с медленно изменяющейся по сравнению с ним входной величиной (управляющим сигналом) приводит, по крайней мере при малых изменениях, к линеаризации релейного элемента, т.е. к тому что среднее значение выходной величины его становится пропорциональной величине х(т). При этих условиях релейный элемент эквивалентен линейному усилителю. Характерная особенность такого усилителя является зависимость коэффициента усиления от амплитуды внешнего воздействия. Увеличение последней уменьшает коэффициент усиления.
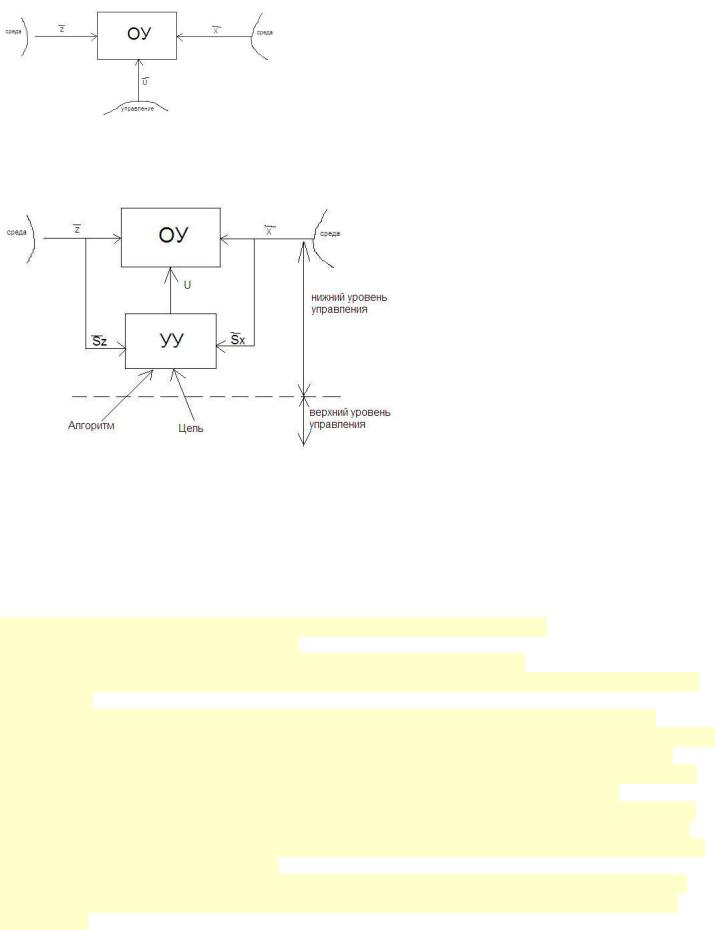
46. Основные определения теории оптимальных систем.
Опр.1. Задачи управления – формализация и реализация для перевода его в нужное состояние. Опр.2. Объект – часть окружающей среды, выделенная так, что выполняется 2 условия:
на объект можно воздействовать; воздействие может изменить состояние объекта в нужном направлении.
Опр.3. Алгоритм управления – совокупность правил, методов и способов, позволяющих синтезировать оптимальное управляющее воздействие на объект в реальных условиях.
Опр.4. Управляющее устройство реализует алгоритм управления.
Опр.5. Система управления – совокупность объектов управления и управляющего воздействия.
Опр.6. Критерий оптимальности – количественная оценка качества функционирования объекта. Опр.7. Целевая функция (функция качества) – формализованное выражения критерия оптимальности.
Опр.8. Оптимальные системы – системы управления, обеспечивающие экстремальное значение критерия при заданных условиях.
Опр.9. Оптимальное управление – соответствующее управление.
47. Этапы решения задач оптимизации.
Постановка задачи на оптимизацию и ее решение включает в себя ряд этапов:
•выбор и обоснование цели оптимизации;
•согласование цели с имеющимися возможностями, т.е. учет ограничений;
•реализация способа достижения цели (экспериментального значения критерия качества ) при учете ограничений.
Выбор и обоснование цели оптимизации предусматривают определение критериев качества (целевых функций), которые наиболее полно отражали бы цели оптимизации. Этот этап является одним из основных, так как от правильности выбора критерия качества зависит решение задачи в целом.
Второй этап решения задачи связан с определением ограничений, которые должны учитываться в процессе оптимизации. Смысл этого этапа заключается в том, что часто качество системы характеризуется не одним, а группой показателей качества, поэтому если система оптимизируется по одному показателю качества, то другие могут достичь такой величины. Следовательно, если выбран какой-либо параметр системы как критерий качества, то на другие показатели качества и варьируемые параметры накладываются ограничения.
При реализации третьего этапа применяется тот или иной метод оптимизации, обеспечивающий решение поставленной задачи - достижение экстремального значения критерия качества при учете ограничений

48. Постановка и классификация детерминированных задач оптимизации.
Под решением задачи понимают процесс выбора управляемых переменных x , принадлежащих допустимой |
||||||||
области D и обеспечивающих оптимальное значение некоторой характеристики объекта F F x . |
|
|||||||
Задача называется задачей оптимизации с ограничениями или задачей условной оптимизации. Задача, в |
||||||||
которой нет ограничений, т.е. |
|
|
|
|
|
|||
m 0 ; |
b |
i |
a |
i |
, i 1, n называется задачей безусловной оптимизации. |
|
||
|
|
|
|
|
|
|
||
Задачи, в которых |
x |
представляет собой одномерный вектор |
n 1 |
, называются задачами одномерной |
|
|||
|
|
|
|
|
|
|
|
|
оптимизации. Если число варьируемых переменных x больше единицы n 2 , то такие задачи являются |
||||||||
задачами многомерной оптимизации, связанными с оптимизацией некоторой n-мерной гиперповерхности |
F x |
|||||||
Задачи условной оптимизации, в которых функции f j x и k x являются линейными, носят название задач с линейными ограничениями. В таких задачах целевые функции могут быть либо линейными, либо нелинейными. Задачи с линейной целевой функцией F x и линейными ограничениями f j x и k x являются задачами линейного программирования (ЗЛП).
Если целевая функция F x - квадратичная функция, а ограничения f j x и k x - линейные функции, то задача (1)-(4) является задачей квадратичного программирования. В тех случаях, когда критерий оптимальности F x или ограничения f j x и k x представляют собой нелинейные функции переменных x , задача (1)-(4) является задачей нелинейного программирования.
49. Многокритериальные задачи оптимизации.
В практике часто возникает необходимость найти решение, которое бы являлось наилучшим с позиций
нескольких различных критериев |
F |
x , |
, F |
x , |
|
, F |
x . |
|
1 |
|
2 |
|
|
k |
|
Решение задачи многокритериальной оптимизации (компромиссное решение) ( x эффективным решением, если для него справедливо неравенство
D
) является
|
|
|
|
F x |
|
x D |
F x |
|
|
,
Первый подход — выбор основного критерия. Один из путей учёта совокупности противоречивых критериев состоит в том, что какой либо из критериев выбирается в качестве основного, а остальные критерии считаются вспомогательными. Оптимизацию осуществляют по основному (одному) критерию, а на все остальные критерии накладывают ограничения.
Второй подход — ранжирование критериев. Пусть критерии ранжированы и номер критерия обозначает номер
ранга. Очевидно, что оптимизацию следует начинать с критерия первого ранга |
|
F1 x min . |
(18) |
x D
Третий подход — формирование обобщённого критерия. Идея этого метода проста: построить обобщённый скалярный критерий
|
|
x , |
|
x , |
, |
|
|
(24) |
F x f F |
F |
F |
x |
|||||
|
1 |
|
2 |
|
|
k |
|
|
как функцию исходных критериев. Пусть минимизируются все частные критерии, чего легко добиться, умножив максимизируемые критерии на -1. При этом минимум обобщённого критерия (24) должен соответствовать
решению многокритериальной задачи. Тогда решение поставленной задачи сведётся к обычной оптимизации |
|
F x min . |
(25) |
x D |
|

50. Одномерная оптимизация.
4.1. Метод равномерного поиска Пусть априорная информация об унимодальности функции крайне недостаточна, чтобы строить разумный
процесс поиска экстремума. Наиболее приемлемым способом поведения в такой обстановке является последовательное вычисление целевой функции I(y) при всех допустимых значениях варьируемого параметра y
a y b ,
где a, b - границы интервалов поиска.
Пусть заданная величина погрешность определения оптимального параметра y*. Тогда для реализации алгоритма поиска следует определить значение I(y) в
N |
b a |
1 |
|
|
|||
|
|
точках, равномерно отстоящих друг от друга на расстоянии h= , т. е. в точках y j a ( j 1) h, j 1,N 1.
Из полученных значений показателя качества I(yj) выбирается наибольшее значение (глобальный максимум). Такой способ поиска называется сканированием. При малой заданной погрешности этот метод требует слишком большое число вычислений функции I(y) и больших затрат машинного времени.
4.2. Метод поразрядного приближения Этот метод применим для поиска оптимума унимодальной функции и обладает более высоким быстродействием.
Это достигается тем, что используется алгоритм с переменным шагом поиска. Вначале величина шага выбирается достаточно большой, значительно превышающей требуемую погрешность определения положения оптимума, и выполняется грубый поиск. В районе оптимума поиск производится с меньшим шагом.
Задается начальное значение параметра y0 = a и вычисляется I0=I(y0). Задаются начальный шаг поиска h и кратность k уменьшения шага в районе оптимума. Производится поиск максимума I(y) из начальной точки y = y0
по алгоритму
y(j+1)=y(j)+h(j+1);
|
|
|
( j) |
, |
при I |
( j) |
|
I |
( j 1) |
; |
|
h |
( j 1) |
h |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h( j) / k, при I( j) |
|
I( j 1), |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
(25)
где j - номер шага.
По этому алгоритму поиск из начальной точки y = y0 осуществляется с постоянным шагом h. После каждого шага вычисляется значение критерия I(y), оно сравнивается с предыдущим значением и в случае улучшения критерия шаги продолжаются до тех пор, пока очередной шаг не окажется неудачным. После этого поиск максимума продолжается из последней точки в обратном направлении с шагом в k раз меньше прежнего. Эта процедура поиска продолжается до тех пор, пока не будет выполнено условие
h ,
где - заданная погрешность определения оптимума. 4.3. Метод дихотомии
Этот метод отыскания экстремума применим для класса унимодальных функций. Идея метода проста - делить интервал [a, b], где расположен оптимум I(y), пополам
y0 = (a + b)/2
и отбрасывать часть, где оптимума заведомо быть не может. С этой целью достаточно вычислить показатель качества I(y) в точках y0 d, отстоящих друг от друга на расстояние 2d < , где - заданная погрешность определения оптимума. По двум вычисленным значениям I(y0 - d) и I(y0 + d), в силу унимодальности функции I(y), легко установить новый интервал неопределенности по следующим условиям (при поиске максимума):
* |
(y0 |
d ) если I(y0 |
d ) I(y0 d ); |
|
|
||||
y |
|
|
|||||||
y* (y |
|
d ) если I(y |
|
d ) I(y |
|
|
|
(26) |
|
0 |
0 |
0 |
d ). |
|
|||||
|
|
|
|
|
|
|
|||
Таким образом, в результате двух вычислений I(y) промежуток, где содержится оптимум, сокращается почти вдвое. Следующая пара измерений проводится в районе середины нового интервала неопределенности [a, y0 + d] или [y0 - d, b] в зависимости от того, какое из условий (26) выполняется.
Аналогично производятся последующие шаги поиска до тех пор, пока на k-ом шаге после 2k измерений I(y) длина интервала неопределенности lk = (b-a)/2k, где находится оптимум, не станет меньше или равен , т. е. lk. 4.4. Метод золотого сечения
В геометрии золотым сечением называется такое деление отрезка на две неравные части, при котором отношение всего отрезка к большей части равнялось отношению большей части к меньшей.

51. Многомерная оптимизация.
Метод наискорейшего спуска представляет собой модификацию градиентного метода и заключается в
определении минимума F x |
, x |
2 |
, , x |
n |
вдоль антиградиентного направления. В основу метода положены |
||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
вычисление и анализ производных целевой функции |
F x |
, x |
2 |
, , x |
n |
|
. |
|
|
|
|
|
|||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
В начальной точке поиска определяем направление вектора градиента F x |
, x |
2 |
, , x |
n |
, для чего |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||
вычисляются частные производные
независимых переменных
F / xi
i 1, n
в точке x x0 , где
x =
x |
, |
1 |
|
x |
, , |
2 |
|
xn
,
- вектор
|
F |
, |
F |
, |
|
, |
F |
||
F x |
x |
x |
|
x |
|
||||
|
|
2 |
|
|
|
n |
|||
1 |
|
|
|
|
|
|
|||
.
Вектор градиента по направлению совпадает с направлением наискорейшего возрастания целевой функции F x . Следовательно, целевая функция в направлении, обратном направлению градиента, т.е. в направлении
антиградиента, убывает наиболее быстро. После того, как в начальной точке найдем градиент оптимизируемой функции и таким образом определим направление её наибыстрейшего убывания, в данном направлении делается
шаг спуска. Если значение функции F x в результате этого шага уменьшилось, производится очередной шаг в
этом же направлении. Аналогичным образом шаги продолжаются до тех пор, пока не будет найден минимум в этом направлении. В новой точке, где достигнут частный минимум в текущем направлении, вновь определяются
частные производные F / xi и новое направление наибыстрейшего убывания F x . Теперь поиск
осуществляется в новом направлении путем анализа величины F x после каждого шага и т.д.
При достаточно большой величине шага в районе оптимума поиск может зациклиться. В этом случае следует
последовательно уменьшить величину h при поиске в районе оптимума.
При использовании рассматриваемого метода можно обнаружить только локальный минимум. Каждый локальный минимум целевой функции можно охарактеризовать некоторой областью притяжения, обладающей тем свойством, что при задании начального состояния в границах этой области метод наискорейшего спуска всегда приводит в один и тот же локальный минимум. Поэтому для поиска других локальных минимумов и выбора среди них глобального необходимо производить поиск из других начальных точек.
52. Линейное программирование.
Линейное программирование представляет собой математический аппарат, разработанный для решения оптимальных задач с линейными выражениями для критерия оптимальности и линейными ограничениями на область изменения переменных. Такие задачи обычно встречаются при решении вопросов оптимального планирования производства с ограниченным количеством ресурсов, при определении оптимального плана перевозок (транспортные задачи) и т.д.
Для решения большого круга задач линейного программирования имеется практически универсальный алгоритм - симплексный, метод, позволяющий за конечное число итераций находить оптимальное решение подавляющего большинства задач. Тип используемых ограничений (равенства или неравенства) не сказывается на возможности применения указанного алгоритма. Дополнительной проверки на оптимальность для получаемых решений не требуется. Как правило, практические задачи линейного программирования отличаются весьма значительным числом независимых переменных. Поэтому для их решения обычно используют вычислительные машины, необходимая мощность которых определяется размерностью решаемой задачи.
