
для Однорала
.docxМинистерство образования и науки Российской Федерации
Новосибирский государственный технический университет
Кафедра аэродинамики
Расчётно – графическая работа №1
по аэрогидрогазодинамике
Факультет: ЛА
Группа: С-21 Преподаватель: Однорал В.П.
Студент: Степанов.К.Б
Вариант: 14
Новосибирск 2014 г.
-
Исходные данные и постановка задачи:
Самолёт с прямоугольным в плане крылом имеет параметры:
|
Масса |
|
37 т. |
|
Размах крыла |
lкр = (25+B/4) |
28.5 м |
|
Плечо ГО |
Lgo = (16 + B/3) |
20.66 м |
|
Площадь крыла |
Skp = (75+ B) |
89 м2 |
|
Высота полёта |
H |
7 км |
|
Скорость полёта |
V = (600+5B) |
670 км/ч |
|
Плотность воздуха (H = 7 км) |
ρ |
0,59 кг/м3 |
|
Скорость звука (а = 7 км) |
а |
308 м/с |
|
Коэффициент адиабаты для воздуха |
k |
1.4 |
|
Ускорение свободного падения |
g |
9.81 м/с2 |
|
Давление (H = 7км) |
Pn |
41098Н/м2 |
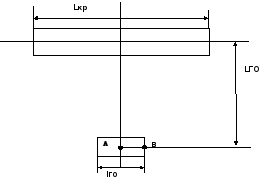
рис. 1
Определить:
1). Углы скоса в центральном и концевом сечениях крыла, приняв П – образную модель вихревой системы крыла.
2). Максимальный перепад давления на обшивке крыла; крыло надувается изнутри полным давлением набегающего потока.
3). Построить эпюру распределения погонной нагрузки по размаху крыла, приняв эллиптический закон распределения циркуляции.
Схему П – образной вихревой системы крыла для центрального сечения горизонтального оперения (для точки А) можно представить в виде:

рис. 2
Схему П – образной вихревой системы крыла для центрального сечения горизонтального оперения (для точки B) можно представить в виде:

рис. 3
Выполнение всех расчётов данной задачи производится с помощью редактора MathCad 14.
Задаём исходные параметры:

Определяем необходимую величину подъёмной силы:

Далее, определяем по формуле Журавского величину циркуляции:

где ρ – плотность воздуха на высоте H = 8000 м; V – скорость полёта самолёта.
Находим углы в центральном сечении крыла (для точки А):

Находим углы в концевом сечении крыла (для точки B):

Вычисляем скорости, индуцированные участками вихря по формуле Био-Савара.
Скорость, индуцированная участком 1, вихревой системы в пределах от θ15 до θ14, для точки А:


где гi -минимальное расстояние от вихря, до рассчитываемой точки.
Скорость, индуцированная участком 2, вихревой системы в пределах от θ13 до θ12, для точки А:
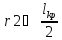

Скорость, индуцированная участком 3, вихревой системы в пределах от θ11 до θ22, для точки А:


Скорость, индуцированная участком 4, вихревой системы в пределах от θ21 до θ23, для точки А:

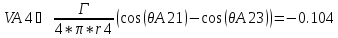
Скорость, индуцированная участком 5, вихревой системы в пределах от θ24 до θ23, для точки А:


Определение скоростей, индуцированных на участках 1-5, для точки B.
Скорость, индуцированная участком 1, вихревой системы в пределах от θ15 до θ14, для точки B:


Скорость, индуцированная участком 2, вихревой системы в пределах от θ13 до θ12, для точки B:


Скорость, индуцированная участком 3, вихревой системы в пределах от θ11 до θ22, для точки B:


Скорость, индуцированная участком 4, вихревой системы в пределах от θ21 до θ23, для точки B:


Скорость, индуцированная участком 5, вихревой системы в пределах от θ24 до θ25, для точки B:


Скорость, индуцированная вихревой системой в точке А:

Скорость, индуцированная вихревой системой в точке B:

Определим угол скоса потока в центральном сечении (точка А):

Определяем
угол скоса потока в концевом сечении
крыла (точка B):

Определение максимального перепада давлений на обшивке:

где q – скоростной напор.
Выполняем построение эпюр распределения погонной нагрузки по размаху крыла.
Принимаем закон распределения циркуляции за эллиптический.
Уравнение эллипса имеет вид:

отсюда

или, выражение для циркуляции:

Площадь сечения S может быть выражена как

Приравнивая
данные выражения, и выразив
 получим:
получим:

Подставляя значение (2) в формулу (1), получим:
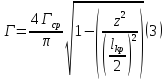
где Гср определим как:

Таким образом окончательно получим выражения для Г(z) и Y(z):


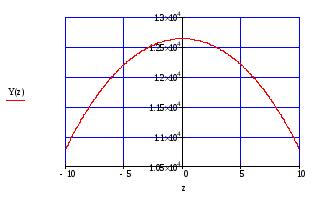

 =
(30+ B/2)
=
(30+ B/2)