24.0. Введение

← 23.5. Способы записи алгоритмов

25.0. Введение →

Линейная алгоритмическая структура отражает последовательность выполнения некоторых действий. Например, при исполнении алгоритма сначала нужно выполнить действие A, затем - действие B, а за ним – действие C. На псевдокоде это может быть записано следующим образом:

… Действие A Действие B Действие C …

Рис. 23.3. Блок схема алгоритма вычисления корней квадратного уравнения

Блок-схема линейной структуры показана на рис. 24.1. Каждое алгоритмическое действие отражается прямоугольником. Размеры сторон прямоугольника a и b могут быть выбраны произвольно, но должны сохраняться во всей блок-схеме и определяют размеры других ее элементов. Переход от одного действия к другому изображается линиями со стрелками. Если линия направлена сверху вниз или справа налево, то стрелки на них допускается не ставить.

Под действием может скрываться элементарное алгоритмическое действие: присваивание, вывод или вывод данных, обращение к вспомогательному алгоритму, а также любая из описанных ниже структурных конструкций или их комбинация. Линейная структура однозначно определяет последовательность действий. В приведенном примере Действие B должно быть выполнено после Действия A и перед Действием C.

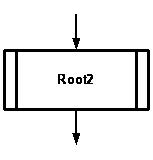
Если действие представляет собой обращение к вспомогательному алгоритму, то на псевдокоде его вызов указывается следующим образом:

… Root2(s,q,r, t1,t2,key) …

На блок-схеме обращение к вспомогательному алгоритму показывается двойными боковыми линиями прямоугольника (рис. 24.2).

Рис. 24.1. Блок-схема линейной алгоритмической структуры	Рис. 24.2. Изображение на блок-схеме обращения к вспомогательному алгоритму

← 23.5. Способы записи алгоритмов

25.0. Введение →

25.0. Введение

← 24.0. Введение

26.0. Введение →

Разветвляющая алгоритмическая структура представляет собой конструкцию, состоящую из двух или более ветвей. Наиболее простой ее вариант – бинарное ветвление (альтернатива, структура if-else, если-то-иначе). Ее блок схема представлена на рис. 25.1 а, а псевдокод – следующим текстом:

… если <логическое выражение> то Ветвь A иначе Ветвь В все …

При ее выполнении сначала вычисляется логическое выражение. Если оно имеет значение истина, то выполняется ветвь A, если же ложь, то ветвь B. Каждая ветвь может включать в себя одно или несколько элементарных действий. Если в ветвь входит несколько действий (операторов), то их необходимо объединить в одно составное действие с помощью служебных слов нач и кон (см. пример алгоритма решения квадратного уравнения). На блок-схеме бинарное ветвление изображается в виде ромбовидного графического элемента альтернатива. Направления перехода могут помечаться также 1 или да (истина) и 0 или нет (ложь).

Частным случаем бинарного ветвления является обход, при котором ветвь иначе не со-держит никакого действия – пустая.

… если <логическое выражение> то Ветвь A все …

Блок-схема этой структуры приведена на рис. 25.1 б.

a	б

Рис. 25.1. Блок-схема структур «ветвление» (а) и «обход» (б)

В качестве логического выражения может быть использовано может быть использовано выражение отношения (условие), в котором два выражения сравниваются знаками отношения, например, k = 0 или i<n или sin(x+π/2)>=exp(-2y)-1. В более сложных случаях в логических выражениях используются знаки логических операций: инверсии not, дизъюнкции or или конъюнкции and. Например, not(k = 0 and ((i<n) or (sin(x+π/2)>=exp(-2y)-1))). При конструировании сложных логических выражений необходимо использовать правила и законы булевой алгебры.

Множественное ветвление представляет собой структуру, разветвляющуюся на более чем две ветви. С точки зрения теоретического программирования она является избыточной, так как может быть реализована с помощью бинарных ветвлений. Но практически все языки программирования имеют оператор, поддерживающий эту структуру, поэтому рассмотрим ее на примере ветвления на три ветви (блок-схема на рис. 25.2). Ветвлением управляет выражение-селектор s, которое может принимать предусмотренные значения a, b и c. Если s = a, то выполняется ветвь A, если s = b, то выполняется ветвь B, и если s = с, то выполняется ветвь С. В структуре также имеется ветвь X, которая будет выполняться, если селектор s примет непредусмотренное для исполнения предыдущих ветвей значение.

На рис. 25.3 показана реализация этой структуры с помощью бинарных ветвлений.

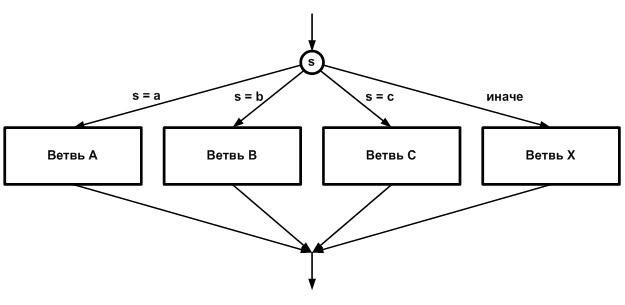
Рис. 25.2. Блок-схема множественного ветвления

Рис. 25.3. Реализация множественного ветвления с помощью бинарных

На псевдокоде множественное ветвление записывается следующим образом:

выбор при s = a: Ветвь A при s = b: Ветвь B при s = c: Ветвь C иначе Ветвь X все

← 24.0. Введение

26.0. Введение →

↑ Наверх