
RGZ_3
.docxМинистерство образования и науки РФ
Новосибирский государственный технический университет
Кафедра ТОЭ
Задание №3
Переходные процессы в цепях с сосредоточенными параметрами
Факультет ФТФ
Группа ФЛ-31 Отметка о защите__________
Студент Гущин А.С. Преподаватель Давыденко О.Б.
Дата выполнения_______
Новосибирск 2014
Задание:
Найти
переходный ток на входе цепи второго
порядка, изображенной на схеме, и
построить график его изменения в функции
времени. ЭДС источника задана в виде

Примечание:
Принужденную составляющую тока рекомендуется найти методом комплексных амплитуд (т.е. символическим методом), а свободную – операторным.
Если наибольшее значение свободной составляющей окажется несоизмеримо малым по сравнению с амплитудой принужденной составляющей, то допускается раздельное построение этих составляющих на чертеже в разных масштабах (без суммирования).
Исходные данные:
n=1 - порядковый номер в группе;
k=1 - номер группы (без первой цифры);
ENT(x) - целая часть числа x;
 -
номер схемы;
-
номер схемы;
 -
номер строки параметров;
-
номер строки параметров;
Параметры:![]()





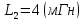

-
Расчет принужденной составляющей.
В соответствии с рекомендациями расчет принужденной составляющей входного тока будем осуществлять методом комплексных амплитуд.
Комплексная
схема замещения для момента времени
 будет иметь вид:
будет иметь вид:



Принуждённую составляющую входного тока можно определить следующим образом:

По правилу делителя токов:
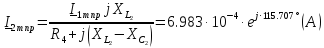
Тогда
ток
 найдём по 1-му закону Кирхгофа:
найдём по 1-му закону Кирхгофа:

Напряжение на конденсаторe

Мгновенные значения токов:



Мгновенное значение напряжения на конденсаторе:

-
Расчёт режима работы цепи до коммутации.
Комплексная
схема замещения для момента времени
 будет иметь вид:
будет иметь вид:






Напряжение на конденсаторе:

Mгновенные значения:
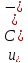
-
Определение независимых начальных условий.
В
соответствии с 1-ым законом коммутации
ток через индуктивный элемент L
непосредственно до коммутации
 равен току через этот же индуктивный
элемент непосредственно после коммутации
равен току через этот же индуктивный
элемент непосредственно после коммутации
 .
.
Из
этого следует:

В
соответствии со 2-ым законом коммутации
напряжение на конденсаторе C
непосредственно до коммутации
 равно напряжению на этом же конденсаторе
непосредственно после коммутации
равно напряжению на этом же конденсаторе
непосредственно после коммутации
 .
Из этого
следует:
.
Из этого
следует:

-
Определение свободных составляющих независимых начальных условий.
Напряжение
на конденсаторе в любой момент времени
переходного процесса представляет
собой сумму принужденной и свободной
составляющих. В частности в момент
времени
 :
:
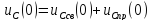

 :
:

Аналогично для тока через индуктивный элемент:

Значение
свободной составляющей тока в момент
времени
 равно:
равно:

-
Определение свободных составляющих операторным методом.
Для
определения свободной составляющей
перейдём к операторной схеме замещения.
Катушка индуктивности заменяется
последовательно соединенными
сопротивлением
 и источником ЭДС, значение которого
равно
и источником ЭДС, значение которого
равно
 . Конденсатор заменяется последовательно
соединёнными сопротивлением
. Конденсатор заменяется последовательно
соединёнными сопротивлением
 и источником ЭДС, значение которого
равно
и источником ЭДС, значение которого
равно
 .
Источник переменного напряжения заменим
на его внутреннее сопротивление, т.е.
закоротим.
.
Источник переменного напряжения заменим
на его внутреннее сопротивление, т.е.
закоротим.
Таким образом, операторная схема замещения имеет вид:

Рассчитаем схему методом узловых потенциалов.
Примем
потенциал узла 0 за ноль:
 .
Тогда:
.
Тогда:

Согласно закону Ома изображение входного тока равно:

Определение оригинала свободной составляющей входного тока
Согласно
теореме разложения, если операторную
функцию
 можно представить в виде отношения двух
многочленов
можно представить в виде отношения двух
многочленов
 (причём многочлен
(причём многочлен
 имеет больший порядок, чем многочлен
имеет больший порядок, чем многочлен
 ),
то изображение для этой функции можно
определить следующим образом:
),
то изображение для этой функции можно
определить следующим образом:
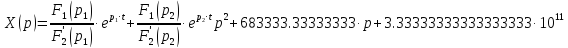
Где
 - корни уравнения
- корни уравнения
 .
.
В нашем случае:
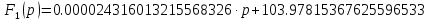

Так
как многочлен
 второго порядка, то свободная составляющая
входного тока будет представлять особую
сумму двух затухающих экспонент (при
условии действительных разных корней
уравнения
второго порядка, то свободная составляющая
входного тока будет представлять особую
сумму двух затухающих экспонент (при
условии действительных разных корней
уравнения
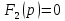 ).
).
В результате решения уравнения получаем:


Найдём производную многочлена в знаменателе:

Вычислим:

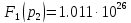


Тогда оригинал свободной составляющей входного тока имеет вид:


-
Графики переходного тока.
Входной ток можно представить как сумму принуждённой и свободной составляющих:

Построим графики каждой из составляющих и полного тока:




-
Проверка решения.
-
Найдём входное сопротивление операторной схемы замещения. Предварительно заменим источники питания в схеме на их внутреннее сопротивление, которое равно 0. В этом случае выражение для входного сопротивления будет иметь вид:

Решив
уравнение
 ,
получаем:
,
получаем:


Как
видно эти значения полностью соответствуют
значениям, полученным в пункте 5 для
уравнения
 .
.
-
Значение входного тока в момент коммутации совпадает со значением полного тока при t=0:

