3. Решение задач линейного программирования средствами пакета MathCad
Задача поиска условного экстремума функции многих переменных часто встречаются в экономических расчётах для минимизации затрат, максимализации прибыли и т. п. При этом экономическая задача описывается системами линейных уравнений и неравенств и относится к задачам линейного программирования. Типичным примером является так называемая транспортная задача, которая решает проблему оптимальной доставки товара потребителям с точки зрения экономии (минимизации) транспортных расходов.
Пусть
у нас имеется N
предприятий-изготовителей, производящих
некоторый продукт в количествах
.
Вся производимая продукция доставляетсяM
потребителям, которые потребляют её в
количестве
.
Отсюда с очевидностью следует, что
.
Затраты на доставку единицы продукции
сi-го
предприятия-изготовителя на j-ое
предприятие-потребитель составляют
.
Если обозначить объём доставляемой
продукции наj-ое
предприятие-потребитель с i-го
предприятия-изготовителя через
,
то общие транспортные расходы можно
найти по формуле
,
где
и
матрица затрат на перевозку единицы
продукции и матрица, элементами которой
является объём перевозимой продукции
между предприятиями соответственно.
Очевидно, что
,
.
Теперь рассмотренную выше транспортную
задачу можно записать формально в
математических терминах. Найти матрицу
,
для которой минимизируемая (целевая)
линейная функция
достигает своего минимума (или максимума)
при следующих ограничениях:
,
,
,
Пример. Три предприятия производят 145, 210 и 160 тонн хлебопродуктов ежедневно. Их реализацией занимаются два торговых объединения, с объёмом продаж 237 и 278 тонн соответственно. Себестоимость доставки тонны продукции задаётся таблицей 3.1. Определить оптимальное с точки зрения минимума затрат на перевозку распределение продукции. Показать, что найденное решение является лучшим. Порядок решения задачи представлен на рис. 3.1.
Таблица 3.1 Транспортные расходы
-
Предприятие-
производитель
1
2
3
Предприятие-
потребитель
1
11.5
7
12
2
6.2
10
9.0
Определяем
векторы
предприятий-производителей
и предприятий-потребителей.
Выполняем
проверку.
Определяем
матрицу
себестоимости
доставки
продукции.
Определяем
целевую
функцию.
Задаём
начальное
приближение.
Задаём
ограничения
.
Матрица
оптимального
товаропотока
и значение целевой функции.
Матрица
неоптимального
товаропотока
и значение целевой функции.
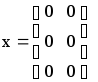
Рис. 3.1. Решение транспортной задачи
Для решения задач оптимизации пакет MathCAD имеет следующие функции:
Minimize(f, var1, var2, …) возвращает значения переменных var1, var2, …, соответствующие минимальному значению функции f;
Maximize(f, var1, var2, …) возвращает значения переменных var1, var2, …, соответствующие максимальному значению функции f;
rows(A) возвращает число столбцов матрицы A.
Задание
В соответствии с заданным вариантом (см. таблицу 3.2) найти оптимальное решение транспортной задачи. Показать, что найденное решение является наилучшим.
Таблица 3.2 Варианты заданий
|
5-я цифра варианта |
Условие транспортной задачи | |||||||||||||||||||||||||||||||||||||||||||
|
0 |
Цех малого предприятия должен изготовить 100 изделий трёх типов. каждого изделия нужно сделать не менее 20 штук. На изделия уходят соответственно 4, 3.4 и 2 кг металла при его общем запасе 340 кг, а также по 4.76, 11 и 2 кг пластмассы при её общем запасе 700 кг. Сколько изделий каждого типа надо выпустить для получения максимального объёма выпуска в денежном выражении, если цена изделий составляет по калькуляции 4, 3 и 2 рубля? | |||||||||||||||||||||||||||||||||||||||||||
|
1 |
В нижеследующей таблице приведены исходные данные транспортной задачи, причём в 12 центральных ячейках указаны тарифы на перевозку единицы груза. Определить наиболее выгодное распределение грузов со складов к скупщикам.
| |||||||||||||||||||||||||||||||||||||||||||
|
2 |
В нижеследующей таблице приведены исходные данные транспортной задачи, причём в 12 центральных ячейках указаны тарифы на перевозку единицы груза. Определить наиболее выгодное распределение грузов от поставщиков к потребителям.
| |||||||||||||||||||||||||||||||||||||||||||
|
3 |
В нижеследующей таблице приведены исходные данные транспортной задачи, причём в 16 центральных ячейках указаны тарифы на перевозку единицы груза. Определить наиболее выгодное распределение грузов от фабрик в пункты назначения.
| |||||||||||||||||||||||||||||||||||||||||||
|
4 |
В нижеследующей таблице приведены исходные данные транспортной задачи, причём в 15 центральных ячейках указаны тарифы на перевозку единицы груза. Определить наиболее выгодное распределение грузов от пунктов отправления к пунктам назначения.
| |||||||||||||||||||||||||||||||||||||||||||
|
5 |
У некого предпринимателя, занимающегося производством и продажей холодильников, есть две фабрики, которые снабжают три его магазина. В начале месяца он получает от директора каждого из магазинов заявку на определенное число холодильников, в которых данный магазин нуждается в текущем месяце. Совокупность всех таких заявок позволяет установить общее число новых холодильников, которые нужно изготовить на этих двух фабриках. Для простоты мы предположим, что у предпринимателя достаточно ресурсов (рабочей силы, сырья и т. д.), чтобы выполнить все заявки, и что в данный момент отсутствует задел для продажи. Пусть первому магазину, обозначим его S1, требуется 10 холодильников, магазину S2 - 8 и магазину S3 - 7, всего, таким образом, 25 холодильников. Пусть предприниматель решил изготовить 11 холодильников на первой фабрике F1 и оставшиеся 14 на фабрике F2. Задача состоит в том, чтобы выяснить, сколько холодильников нужно отправить с каждой фабрики в каждый магазин, чтобы общая стоимость всех перевозок была минимальной. Матрица транспортных расходов С
| |||||||||||||||||||||||||||||||||||||||||||
|
6 |
Cosmic Computer Company (CCC) имеет три сборочных компьютерных завода, расположенных в Сан-Франциско, Лос Анжелесе и Фениксе. Завод в Лос Анжелесе может собирать в месяц до 2000 компьютеров, заводы в Сан-Франциско и Фениксе до 1700. Продукцией ССС торгуют четыре розничных магазина, находящиеся в Сан-Диего, Таксоне, Барстоу и Далласе. Объем заказов на планируемый месяц составляет 1700 компьютеров в Сан-Диего, 1000 в Барстоу, 1500 в Таксоне и 1200 в Далласе. Стоимости доставки одного компьютера из места сборки в место продажи (в $/ед.) или, как принято говорить, транспортные тарифы, приведены в следующей таблице
Определить наиболее выгодное распределение компьютеров по магазинам. | |||||||||||||||||||||||||||||||||||||||||||
|
7 |
В нижеследующей таблице приведены исходные данные транспортной задачи, причём в 12 центральных ячейках указаны тарифы на перевозку единицы груза. Определить наиболее выгодное распределение грузов от поставщиков к потребителям.
| |||||||||||||||||||||||||||||||||||||||||||
|
8 |
В нижеследующей таблице приведены исходные данные транспортной задачи, причём в 12 центральных ячейках указаны тарифы на перевозку единицы груза. Определить наиболее выгодное распределение грузов от поставщиков к потребителям.
| |||||||||||||||||||||||||||||||||||||||||||
|
9 |
Для строительства четырех объектов используется кирпич, изготавливаемый на трех заводах. Ежедневно каждый из заводов может изготовить 100, 150 и 50 условных единиц кирпича (предложение поставщиков). Потребности в кирпиче на каждом из строящихся объектов ежедневно составляют 75, 80, 60 и 85 условных единиц (спрос потребителей). Тарифы перевозок одной условной единицы кирпича с каждого из заводов к каждому из строящихся объектов задаются матрицей транспортных расходов
Требуется составить такой план перевозок кирпича к строящимся объектам, при котором общая стоимость перевозок будет минимальной. | |||||||||||||||||||||||||||||||||||||||||||
|
a |
В нижеследующей таблице приведены исходные данные транспортной задачи, причём в 15 центральных ячейках указаны тарифы на перевозку единицы груза. Определить наиболее выгодное распределение грузов от пунктов отправления к пунктам назначения.
| |||||||||||||||||||||||||||||||||||||||||||
|
b |
В нижеследующей таблице приведены исходные данные транспортной задачи, причём в 12 центральных ячейках указаны тарифы на перевозку единицы груза. Определить наиболее выгодное распределение грузов от поставщиков к потребителям.
| |||||||||||||||||||||||||||||||||||||||||||
|
c |
В нижеследующей таблице приведены исходные данные транспортной задачи, причём в 12 центральных ячейках указаны тарифы на перевозку единицы груза. Определить наиболее выгодное распределение грузов со складов к скупщикам.
| |||||||||||||||||||||||||||||||||||||||||||
|
d |
Два завода снабжают три магазина телевизорами. В начале месяца они получают от каждого из магазинов заявки на определенное число телевизоров, в которых данный магазин нуждается в текущем месяце. Совокупность всех таких заявок позволяет установить общее число новых телевизоров, которые нужно изготовить на этих двух заводах. Пусть первому магазину, обозначим его M1, требуется 10 телевизоров, магазину M2 - 8 и магазину M3 - 7, всего, таким образом, 25 телевизоров. Пусть первый завод решил изготовить 11 телевизоров, а оставшиеся 14 второй завод. Задача состоит в том, чтобы выяснить, сколько телевизоров нужно отправить с каждой фабрики в каждый магазин, чтобы общая стоимость всех перевозок была минимальной. Матрица транспортных расходов С
| |||||||||||||||||||||||||||||||||||||||||||
|
e |
Для строительства четырех объектов используется кирпич, изготавливаемый на трех заводах. Ежедневно каждый из заводов может изготовить 200, 300 и 100 условных единиц кирпича (предложение поставщиков). Потребности в кирпиче на каждом из строящихся объектов ежедневно составляют 150, 160, 120 и 170 условных единиц (спрос потребителей). Тарифы перевозок одной условной единицы кирпича с каждого из заводов к каждому из строящихся объектов задаются матрицей транспортных расходов С.
Требуется составить такой план перевозок кирпича к строящимся объектам, при котором общая стоимость перевозок будет минимальной. | |||||||||||||||||||||||||||||||||||||||||||
|
f |
Предприятие должно изготовить 300 изделий трёх типов. каждого изделия нужно сделать не менее 40 штук. На изделия уходят соответственно 4, 3.4 и 2 кг металла при его общем запасе 940 кг, а также по 4.76, 11 и 2 кг пластмассы при её общем запасе 2100 кг. Сколько изделий каждого типа надо выпустить для получения максимального объёма выпуска в денежном выражении, если цена изделий составляет по калькуляции 4, 3 и 2 рубля? | |||||||||||||||||||||||||||||||||||||||||||
.
Отчётность по расчётно-графическому заданию
Отчёт предоставляется в виде распечатки файла формата MS Word 2000. Отдельно к отчёту прилагаются его электронная версия и файлы кодов программ для пакета Mathcad 2000. Приложения должны быть оформлены в виде папки (каталога). Отчёт должен включать в себя: титульный лист; текст задания; текст кода программ(ы) с подробными комментариями; выводы, отражающие мнение студента о достоинствах и недостатках пакета Mathcad 2000 для решения задач вычислительной математики. Размер символов (Times New Roman) в отчёте и приложениях – не менее 12 пт.