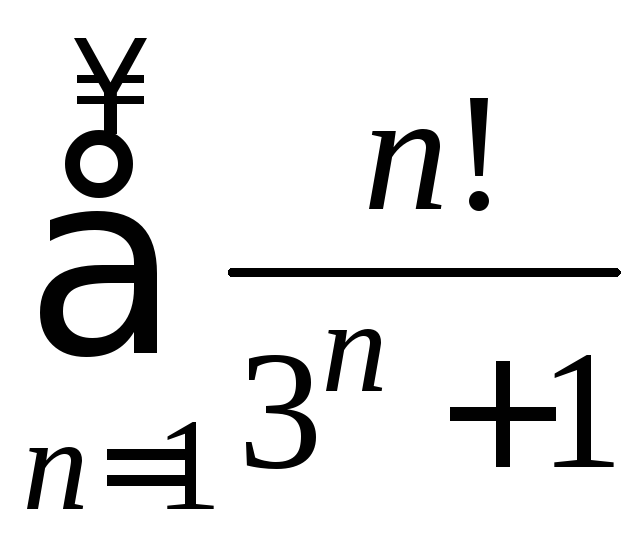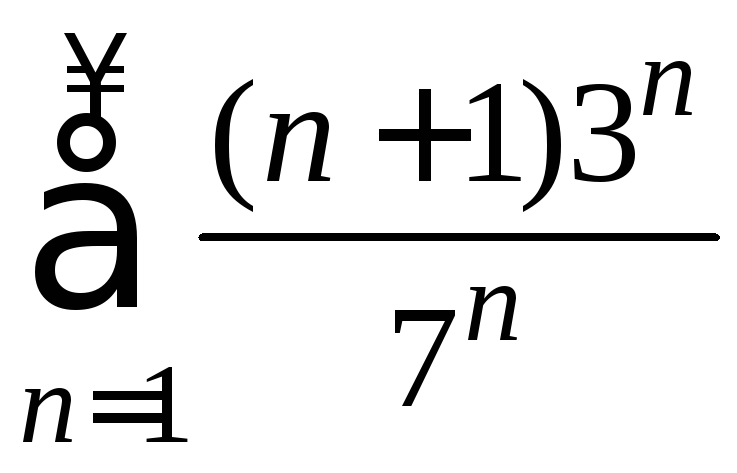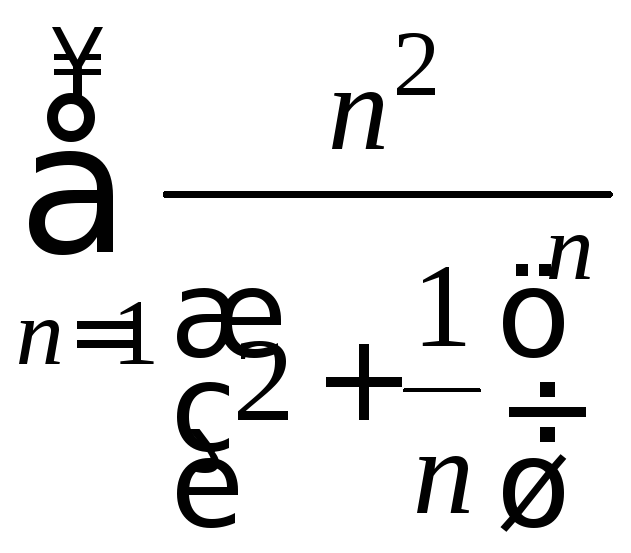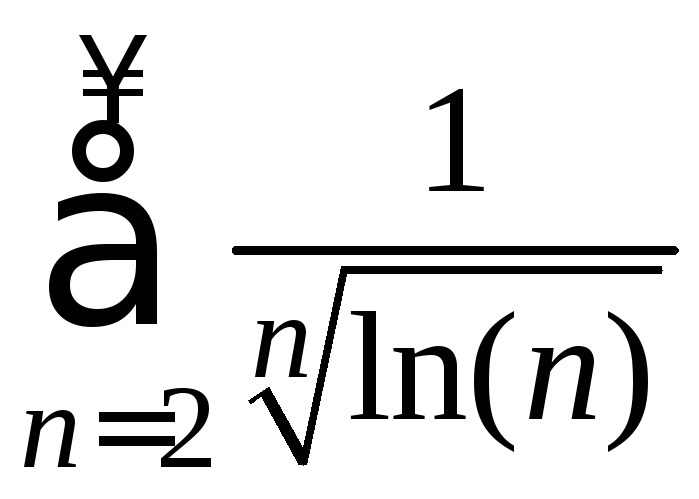2. Исследование числовых рядов

Пусть ,,, …,, …, где− бесконечная числовая последовательность. Выражение

называют бесконечным числовым рядом, а числа ,,, …,, … − членами ряда;называется общим членом. Суммаn первых членов называется n-ой частичной суммой ряда .

Ряд 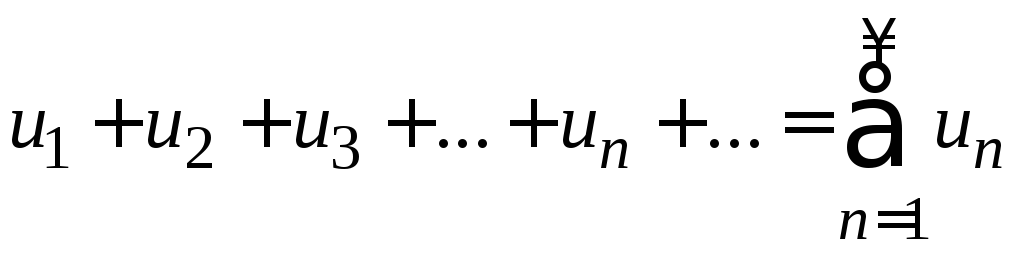называется сходящимся, если егоn-ая частичная сумма при неограниченном возрастании n стремится к конечному пределу, т. е. если . ЧислоS называют суммой ряда. Если n-ая частичная сумма ряда при не стремится к конечному пределу, то ряд называется расходящимся.

Справедливо следующее утверждение (необходимый признак сходимости ряда). Для того чтобы ряд сходился, необходимо, чтобы последовательность его членовстремилась к нулю при, т. е.. Обратное, вообще говоря, неверно. Члены ряда могут стремиться к нулю, но ряд при этом расходится.

На рис. 2.1 приведён фрагмент рабочего документа MathCAD, содержащий исследование расходящегося и сходящегося рядов; для каждого исследуемого ряда построен график последовательности частичных сумм и членов ряда.

Указание. Для того чтобы вычислить символьно сумму ряда или пределв панели, следует щёлкнуть по кнопкев панелии по рабочему документу вне выделяющей рамки.

Перечислим важнейшие признаки сходимости и расходимости рядов с положительными членами.

Гармонический ряд

Ряд расходится.

Необходимый признак сходимости

ряда выполняется.

Ряд Лейбница

Ряд сходится.

Необходимый признак сходимости

ряда выполняется.

Тем не менее,

сумму ряда MathCAD

символьно не

вычисляет!

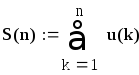
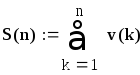
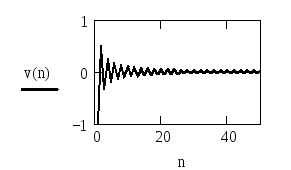
Рис. 2.1. Фрагмент рабочего документа MathCAD, содержащий

исследование расходящегося и сходящегося рядов

1. Первый признак сравнения. Рассмотрим два числовых ряда с неотрицательными членами и,,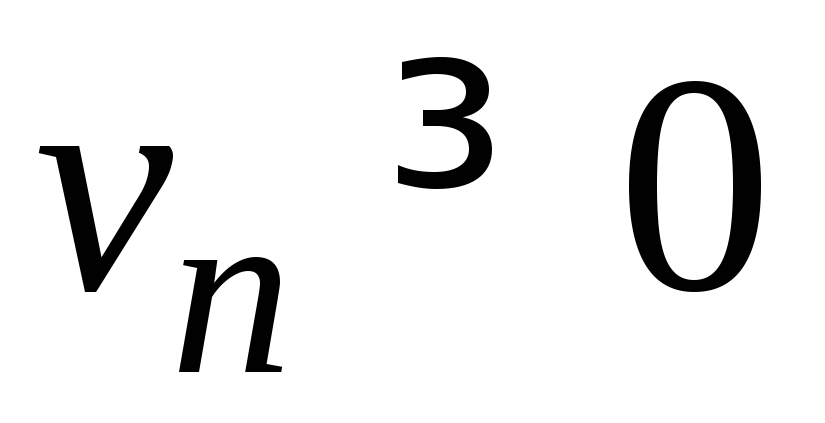. Если для всехn, начиная с некоторого, справедливо неравенство 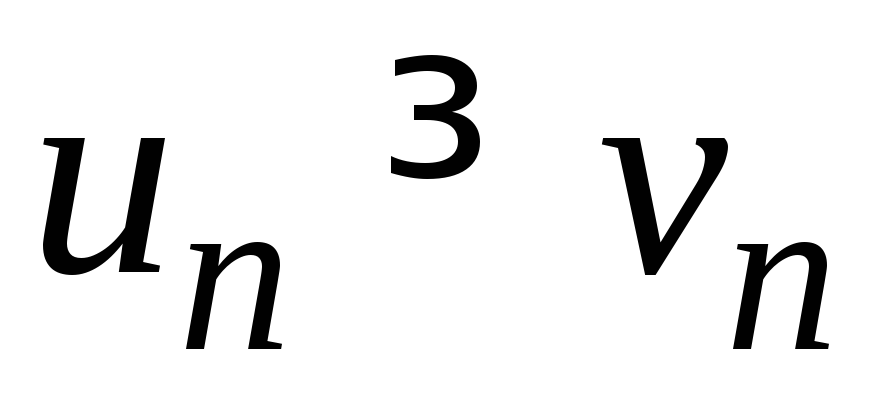, то из сходимости рядаследует сходимость ряда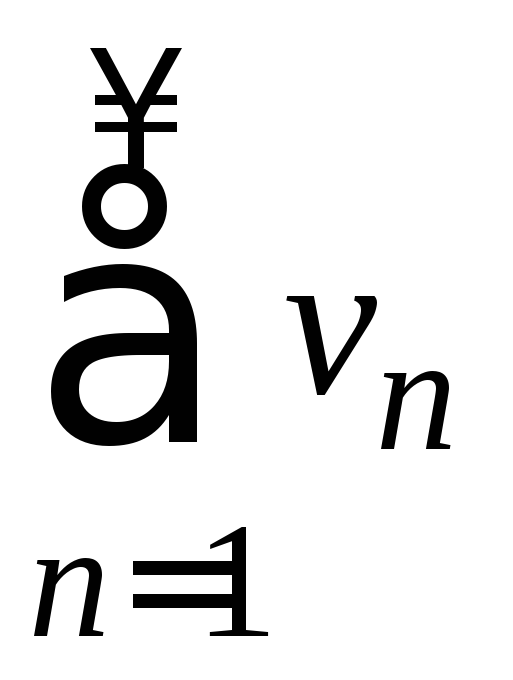; и наоборот, из расходимости рядаследует расходимость ряда.

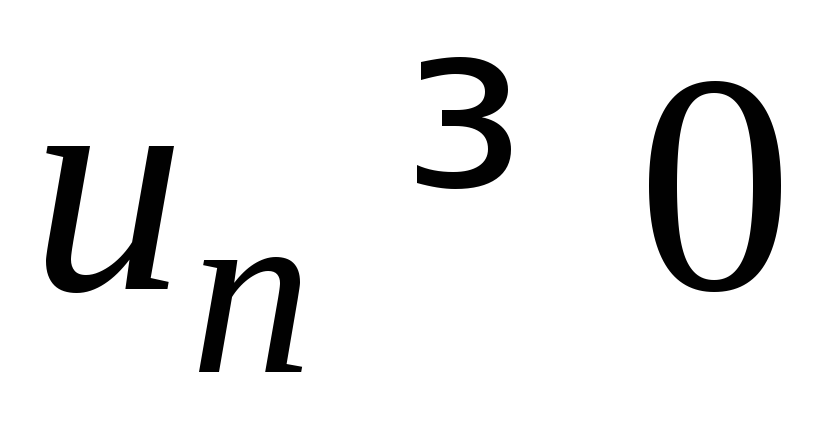2. Второй признак сравнения. Рассмотрим два числовых ряда с неотрицательными членами и,,. Если, то рядыисходятся или расходятся одновременно.

При использовании теорем сравнения исследуемый ряд чаще всего сравнивают с простейшими рядами − с обобщённым гармоническим рядом (, который сходится прии расходится при) или с рядом типа прогрессии (,который сходится прии расходится при).

На рис. 2.2 приведён фрагмент рабочего документа MathCAD, содержащий исследования сходимости рядов на основе теорем сравнения.

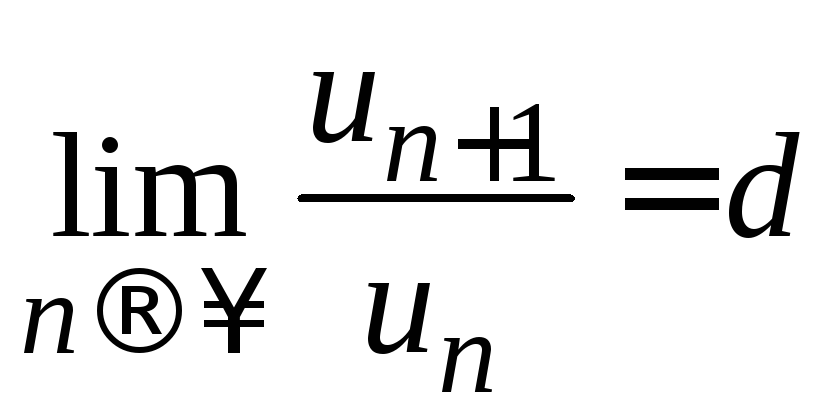3. Признак сходимости Даламбера. Для ряда с положительными членами ,, вычислим предел. Если, то рядсходится, если− расходится. Привопрос о сходимости ряда остаётся открытым: ряд может оказаться как сходящимся, так и расходящимся.

4. Признак сходимости Коши. Для ряда с положительными членами ,, вычислим предел. Если, то рядсходится, если− расходится. Привопрос о сходимости ряда остаётся открытым: ряд может оказаться как сходящимся, так и расходящимся.

Рис. 2.2. Исследование сходимости рядов на основе теорем сравнения

На рис. 2.3 приведён фрагмент рабочего документа MathCAD, содержащий исследования сходимости рядов ис использованием признаков сходимости Даламбера и Коши.

Ряд сходится по признаку

сходимости Даламбера.

Ряд сходится по признаку

сходимости Коши.

Сумма ряда символьно не вычисляется.

Рис. 2.3. Исследование сходимости рядов на основе признаков

сравнения Даламбера и Коши

Задание

2.1. Выяснить, выполняется ли необходимый признак сходимости рядов. Вычислить сумму ряда. Построить (по возможности) графики для величин членов ряда и его n-ой частичной суммы (). Вариант взять из таблицы 2.1.

2.2. Исследовать сходимость ряда, используя один из признаков сходимости. Построить (по возможности) графики для величин членов ряда и его n-ой частичной суммы (). Вариант взять из таблицы 2.2.

Таблица 2.1 Вид числовых рядов

3-я цифра варианта	Вид ряда	3-я цифра варианта	Вид ряда
0		8
1		9
2		a
3		b
4		c
5		d
6		e
7		f

Таблица 2.2 Вид числовых рядов

4-я цифра варианта	Вид ряда	4-я цифра варианта	Вид ряда
0		8
1		9
2		a
3		b
4		c
5		d
6		e
7		f