ИИС СПОСОБЫ РЕШЕНИЯ ЗАДАЧ

СПОСОБЫ РЕШЕНИЯ ЗАДАЧ

Процесс решения задачи, как правило, включает два этапа: представление задачи и поиск (перебор). Успех решения задачи в значительной мере определяет­ся формой ее представления. Формы или способы пред­ставления задачи могут быть различными и зависят как от природы самой задачи, так и от ее решателя. Например, при вычислении интеграла человек стремится путем преобразований представить его так, чтобы вос­пользоваться табличными интегралами. Выбирая крат­чайший маршрут движения, человек может воспользо­ваться схемным представлением возможных путей пере­мещения и опенками расстояний между промежуточны­ми пунктами. Однако характер человеческого мышления таков, что этап и форма представления задачи, которую он использует, не всегда им осознаются. Так, шахматист не может четко объяснить форму представления шах­матной ситуации, позволяющую ему не перебирать все возможные варианты продолжения при поиске очередно­го хода. Поэтому этап представления задачи часто выпадает из поля зрения человека. Тем не менее важность этого этапа осознается сразу же при попытке построить программно реализуемый алгоритм решения задачи.

3.1. Способы представления задач

Поиск формы представления задачи, удобной для ее машинного решения, является трудно формализуемым творческим процессом. Можно выделить следующие наиболее употребительные формы: представление пространстве состояний; представление путем сведена задачи к подзадачам; представление в виде теоремы; комбинированное представление.

Представление задач в пространстве состояний. Пол­ное представление задачи в пространстве состояний

66

включает описание всех состояний или только началь­ных, задание операторов, отображающих одни состоя­ния в другие, и задание целевого состояния. Возможны различные формы описания состояний задачи. В част­ности, могут быть использованы строки, векторы, матри­цы и графы. Выбирая ту или иную форму описания состояний, следует позаботиться о том, чтобы приме­нение оператора, преобразующего одно состояние в дру­гое, оказалось достаточно простым.

Операторы могут быть заданы с помощью таблицы, связывающей каждое «входное» состояние с некоторым «выходным». Для больших задач такое задание опера­тора практически непригодно. При описании состояний в форме строки (вектора) удобно задать оператор в виде правила переписывания.

Процедура поиска решения в пространстве состоя­ний состоит в том, чтобы найти последовательность операторов, которая преобразует начальное состояние в целевое, т. е. в состояние, отвечающее поставленной цели. Решением задачи будет указанная последователь­ность операторов.

Из изложенного ясно, что представление задачи в пространстве состояний определяется совокупностью трех составляющих — тройкой (So, F, G), где So — множество начальных состояний; F — множество операторов, ото­бражающих одно состояние в другое (т. е. пространство состояний в себя), G — множество целевых состоя­ний.

Задача о выборе маршрута, или зада­ча о коммивояжере.

Транспортный робот должен построить маршрут так, чтобы побывать в каждом из п заданных пунктов в точности по разу и возвратиться в исходный пункт. При этом, если таких маршрутов несколько, жела­тельно выбрать такой, который имеет минимальную протяжен­ность. На рис. 3.1 приведено схе­матическое изображение распо­ложения пунктов А, В, С, D, марш­рутов и расстояний.

Состояния в этой задаче можно задавать строкой, обозначающей список пунктов, пройденных к те­ кущему моменту. Так, если робот р_ие. 3.1. Cxeva начинает маршрут из пункта А, маршрутоь

67

то начальным состоянием будет строка из одной буквы а Не допускается, чтобы в строке какой-либо пункт упоми нался более одного раза. Исключением является строка в которой в конце повторно упоминается А, после того как перечислены (упомянуты) все остальные пункты.

Операторы — это отображения, соответствующие ре шению робота направиться из данного пункта в какой-либо следующий. Целевым состоянием, если не требуется минимизировать протяженность маршрута, является любое состояние, описание которого начинается и кон-чается А и содержит названия всех других пунктов Таким, например, является состояние ABCDA.

Задача о манипуляции предметами Пусть состояние, или, как принято говорить, мир задачи включает некоторое число площадок с расположенными на них кубиками (в реальной задаче вместо кубиков могут рассматриваться детали, из которых необходимо собрать изделие), а также робот-манипулятор, пере­мещающий кубики с одной площадки на другую и устанавливающий их друг на друга. Текущее состояние такого мира можно интерпретировать как текущее рас­положение кубиков на площадках и положение манипу­лятора. Совокупность всех возможных состояний об­разует множество S. Очевидно, способы перемещения кубиков роботом, т. е. переход от одного состояния к другому, должны быть подчинены некоторым требова­ниям. Так, может быть ограничено число кубиков на конкретной площадке. Для перемещения естественно выбирать кубики, лежащие сверху, и т. д. На основе таких требований строится множество F допустимых операторов преобразований мира, которые фактически являются совокупностью разрешенных действий робота. Желаемое расположение кубиков на площадках есть целевое состояние мира. Решением задачи является последовательность действий робота (цепочка операто­ров F\, ..,., F_n), с помощью которой можно переставить кубики из некоторого начального расположения (на­чальное состояние мира) в желаемое, т. е целевое состояние. Часто описанную задачу называют задачей преобразования сцен.

Планирование работы гибкого про-изводственного участка. Рассмотрим гибкий производственный участок, состоящий из нескольких механообрабатывающих центров (в общем случае раз­личных), транспортной тележки и автоматизированною

68

склада. На участке требуется обработать N деталей m различных типов за время, не превышающее T. На- яльное состояние системы — все заготовки, необходи- мые для изготовления деталей, находятся на складе, обрабатывающие центры и транспортная тележка на- ходятся в определенном состоянии. Целевое состояние - все заготовки прошли обработку в заданном техноло­ гическим маршрутом порядке на соответствующих обра­ батывающих центрах. Текущее состояние системы опре­ деляется числом и типом обработанных деталей, состоя­ ниями обрабатывающих центров и транспортной тележ­ ки, а состояние обрабатывающего центра — типом дета­ ли, которую в данный момент он обрабатывает (ожида­ ние детали и отказ обрабатывающего центра также являются его определенными состояниями). Состояние тележки зависит от того, где она располагается, какой деталью она загружена в данный момент, движется или находится в режиме ожидания вызова. Множество опе­ раторов F формируется с учетом требований техноло­ гического маршрута, настройки обрабатывающих цент­ ров, возможностей транспортной тележки. Каждое перемещение детали с одного центра на другой, оче­ видно, является сменой состояний. Решением задачи будет последовательность операторов F , F_n, организу­ ющих изменение состояния системы (перемещение дета­ лей между центрами их обработки) таким образом, что все детали будут обработаны за время, не пре­ вышающее Т.

Граф. При описании пространства состояний и методов поиска решений в искусственном интеллекте широко используются граф и особенно одна его раз­новидность, называемая деревом.

Графом (или геометрическим графом) называется геометрическая конфигурация, состоящая из множест­ва V точек, взаимосвязанных с множеством Е непре­рывных, самонепересекающихся кривых [2]. Точки из множества V называются вершинами, а кривые из мно­жества Е — ребрами. Общими точками ребер могут быть только вершины (т. е. точки из множества V). Если на всех ребрах задано направление, указываемое стрелкой, то граф называется ориентированным графом или орграфом, а его ребра — дугами. Если заданы Два графа G1 и G2, причем множества вершин и кривых графа G2 являются подмножествами множеств вершин И кривых графа G1 соответственно, то граф G2 назы-

69

вается подграфом графа G1, а граф G1 —надграфом графа G2- Последовательность различных дуг d1, ....dn.. для которой конечная вершина v1, дуги d1 является начальной вершиной дуги d(i+1)(i= 1, ...,n — 1), называет­ся путем от вершины v0 к вершине vn (v0—начальная вершина дуги d1, v_n — конечная вершина дуги dn).

Деревoм называется орграф, в каждую вершину которого входит только одна дуга, за исключением одной вершины, называемой корнем дерева. В корень не входит ни одна дуга. Таким образом, в дереве каждая вершина, за исключением корня, является концом ровно одной дуги и началом одной или нескольких других дуг, а ко-рень — только началом одной или нескольких дуг. Все дуги, выходящие из одной вершины, называются ветвью этой вершины. Если v — какая-либо вершина дерева и вершины v, (i=1,..,m) являются концами дуг, выходя-ших из вершины v, то будем считать, что вершины у. порождаются вершиной v или вершина v порождает вершины vi. Иногда вершину v (по отношению к верши-нам vi) называют родительской, а вершины vi (по отно­шению к вершине v) — дочерними вершинами или прием­никами.

Введем понятие уровня. Примем, что корень находит­ся на нулевом уровне; вершины, порожденные корнем, -на первом уровне; вершины, порожденные вершинами k-го уровня, — на (k+1)-м уровне.

Представление, сводящее задачу к подзадачам. Такое представление предусматривает разбиение исход-ной задачи на множество подзадач, раздельное решение которых дает решение исходной задачи. Каждая из под­задач может, в свою очередь, быть также разбита на подзадачи. Число уровней разбиения теоретически не ограничено. На практике разбиение продолжается до получения на нижнем уровне множества задач (подза­дач), способ решения которых известен. Такие задачи условимся называть элементарными.

Существуют два типа структур взаимосвязи подза­дач: И-структуры и И—ИЛИ-структуры. В структурах типа И для решения основной задачи требуется решить все подзадачи. В структурах И—ИЛИ подзадачи разби­ваются на группы, внутри которых они связаны отноше­нием И, а между группами — отношением ИЛИ. В этом случае для решения исходной задачи достаточно решить все подзадачи только какой-либо одной группы.

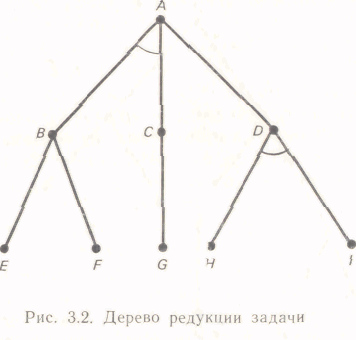
Для описания представления сведения задач к подза­дачам можно использовать граф, называемый графом редукции задачи. При этом вершинам будут соответство-вать задачи, а дугам — операторы редукции задач. Причем корню дерева соответствует исходная задача, вершинам 1-го уровня — задачи, непосредственно по-рожденные исходной задачей, вершинам 2-го уровня -задачи, порожденные задачами 1-го уровня, и т. д.

Предположим, что задача А может быть решена, если будут решены задачи б и С или задача D; задача B будет решена, если будут решены задачи Е или F; зада­ча С — если решена С; задача D — если решены // и /. Граф такого представления задачи А приведен на рис. 3.2. Вершины B и С связаны в том смысле, что для решения задачи А необходимо решить обе задачи В и С. Связанными в этом смысле являются также верши­ны // и /. Для указания связанности каких-либо вершин дуги, входящие в эти вершины, соединяются специаль­ной кривой. Если имеются связанные вершины (дуги), то обычно, вводя при необходимости дополнительные вершины, дерево редукции задачи преобразуют так, чтобы каждая группа связанных вершин имела отдель­ную родительскую вершину. На рис, 3.2 связанные вершины В и С имеют общую с О родительскую верши­ну А. После преобразования этого дерева в соответствии с указанным требованием (введением дополнительной вершины К) получим дерево, изображенное на рис. 3.3, В котором каждая группа связанных вершин имеет

71

отдельную родительскую вершину. Далее рассматривают­ся деревья редукции задачи только такого типа.

Структурно граф (дерево) редукции задачи отлича-ется от графа (дерева) состояния тем, что в нем имеют­ся связанные дуги. Связанные вершины также называ­ют И-вершинами, а несвязанные— ИЛИ-вершинами, а граф, содержащий И- и ИЛИ-вершины, — графом типа И — ИЛИ. Вершины, соответствующие элементарным задачам, называются заключительными Z. Вершины, не имеющие дочерних вершин и не являющиеся заключи­тельными, будем называть тупиковыми. Тупиковым вершинам соответствуют задачи, которые в рамках дан­ного представления не разрешимы, т. е. не могут быть решены. Вершины, которым соответствуют разрешимые задачи, называют разрешимыми, а вершины, которым соответствуют неразрешимые задачи — неразрешимыми. В соответствии с этим заключительные вершины являют­ся разрешимыми, а тупиковые — неразрешимыми. Вер­шина, не являющаяся ни заключительной, ни тупико-вой, будет разрешимой тогда и только тогда, когда все-ее дочерние вершины разрешимы, если они являются связанными, или хотя бы одна из дочерних вер­шин разрешима, если они являются несвязанными. Оче­видно, задача А (рис. 3.3) является разрешимой в том и только в том случае, если вершины H и I являются

72

заключительными или заключительными являются вер­шины С и Г или вершина Е.

Граф редукции задачи может быть задан в явном виде, как в рассмотренном примере. Но чаще он, как и граф состояния, задается в неявном виде посредством описания исходной задачи и операторов редукции.

Представление в виде теорем. Многие задачи (ло­гического типа и др.) могут быть сформулированы как теоремы, подлежащие доказательству. К доказательству теорем могут быть сведены головоломки, игровые задачи, а также ряд практических задач, таких, как принятие решений, планирование действий.

При представлении задачи в виде теоремы определя­ются или задаются посылки, т. е. множество известных истинных утверждений (аксиом). Затем формулируется теорема, доказательство которой позволяет получить решение исходной задачи. Поиск решения при таком представлении производится следующим образом. Ком­бинируя по-разному две аксиомы или более, выводятся утверждения, которые можно получить из посылок. За­тем проверяется, не содержит ли полученное множество утверждений теорему или ее отрицание. Если содержит, то теорема доказана или соответственно отвергнута. Если теорема или ее отрицание не содержится, то полу­ченное множество утверждений добавляется к посылкам i и процедура повторяется. Такой метод поиска решения (доказательства) фактически является методом полного перебора. Если подлежащая доказательству теорема или ее отрицание могут быть выведены из исходных посы­лок, то методом полного перебора всегда можно полу­чить искомое доказательство через конечное число шагов. Но практически применение этого метода ограничено, так как при полном переборе может потребоваться чрезмерно большой объем памяти и большое время решения.

Комбинированное представление. В общем случае необязательно использовать какое-либо одно представле­ние. Более эффективным при решении отдельных задач может оказаться комбинированное (т. е. смешанное) представление. Например, если задача имеет явно выра­женную иерархическую структуру и легко разбивается на ряд подзадач, то естественно сначала свести задачи к подзадачам, а для представления подзадач исполь­зовать различные формы описания в пространстве со­стояний или представление в виде теоремы.

73

3.2. Поиск решений в пространстве состояний

Поиск решений в пространстве состояний сводится к определению последовательности операторов, отобра­жающих начальные состояния в целевые. Причем если такая последовательность операторов не одна и задан критерий оптимальности, то поиск сводится к нахожде­нию оптимальной последовательности, т. е. последова­тельности операторов, обеспечивающей оптимум задан­ного критерия оптимальности. Методы поиска решений в пространстве состояний удобно рассмотреть, используя дерево (граф) состояний. На дереве состояний поиск решения сводится к определению пути (оптимального, если задан критерий оптимальности) от корня дерева к целевой вершине, т. е. к вершине, соответствующей целевому состоянию. Поиск решения можно наглядно проиллюстрировать на дереве состояний, когда началь­ное состояние одно. Поэтому сначала рассмотрим зада­чи, определяемые тройкой (So, F, G), в которой мно­жество So начальных состояний состоит из одного эле­мента. Напомним, что в указанной тройке F -- множе­ство операторов, отображающих пространство состояний в себя; G — множество целевых состояний.

Для построения дерева состояния следует, используя операторы из F, применимые к корню дерева (началь­ному состоянию), построить вершины 1-го уровня. Затем, используя операторы из F, применимые к вершинам 1-го уровня, построить вершины 2-го уровня и т. д. Процесс применения операторов к какой-либо вершине дерева для построения всех ее дочерних вершин назы­вается раскрытием вершины. Поэтому операторы преоб­разования мира (операторы из F) интерпретируются как правила раскрытия вершин. Применение правил рас­крытия к начальной вершине порождает совокупность дочерних вершин. Каждая из них соответствует некото­рому состоянию мира, в которое он может перейти из начального состояния. Дуги, связывающие начальную вершину с дочерней, идентифицируются как соответ­ствующие операторы преобразования. Для всех дочерних вершин производится проверка, не являются ли они целевыми, т. е. не соответствуют ли целевым состоя­ниям. Если целевая вершина не обнаружена, то выпол­няется следующий этап порождения вершин путем при­менения правил раскрытия к каждой вершине, порожден­ной на предыдущем этапе. Полученное множество

74

вершин также анализируется на присутствие целевой вершины. Процедура продолжается до обнаружения це­левой вершины.

Рассмотрим процедуру построения графа состояний на примере выбора маршрута транспортным роботом, который должен, выйдя из склада (пункта А), обойти обрабатывающие центры (пункты В, С, D) и вернуться в склад. Запрещается, чтобы робот побывал в каком-либо из обрабатывающих центров более одного раза. Схема маршрутов и расстояние между пунктами пред­ставлены на рис. 3.1.

Условимся состояние в этой задаче обозначать сло­вом (набором букв), образованным из букв, соответ­ствующих наименованию пунктов, пройденных к текуще­му моменту, и расположенных в том порядке, в каком были пройдены соответствующие пункты. Тогда, оче-

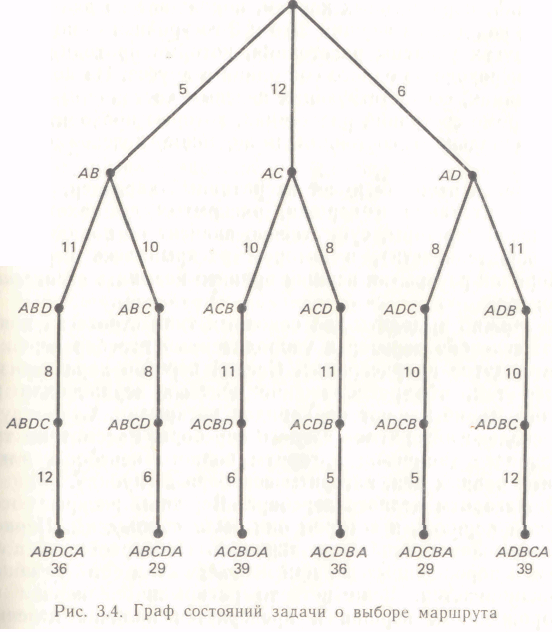
видно, начальным будет состояние А, а целевыми будут состояния, которые обозначаются словами, начинаю­щимися и кончающимися буквой А и включающими по одному разу наименования всех остальных пунктов. Состояния, кроме целевых, которые описываются слова­ми, содержащими повторяющиеся буквы, являются недо­пустимыми.

Операторы (или правила раскрытия) в данном при­мере соответствуют выбору того или иного маршрута. Так как из каждого пункта можно попасть в любые три другие пункта, то множество состоит из 12 опера­торов. Причем применимыми к любому данному состоя­нию являются не более трех операторов.

На графе состояний этой задачи (рис, 3.4) началь­ной вершине (корню дерева) соответствует состояние А. Корень дерева порождает три дочерние вершины, соот­ветствующие состояниям АВ, АС и АD. Каждая из вершин, порожденных корнем, порождает по две верши­ны и каждая из вершин 2-го и 3-го уровнен — по одной. На дугах указаны расстояния, которые проходит робот при переходе из одного состояния в другое. На концевых вершинах, соответствующих целевым состояниям, указа­ны кроме состояний расстояния, которые проходит робот из начального состояния в заданное целевое состоя­ние.

Поиск решения имеет итеративный характер, причем число итераций и вершин, раскрытых до нахождения целевой вершины, существенно зависит от порядка (по­следовательности), в котором раскрывались вершины. Порядок раскрытия вершин принято называть стратегией поиска.

Можно выделить два основных типа стратегий поис­ка: «слепой» перебор и упорядоченный перебор вершин-кандидатов на раскрытие. Слепой перебор характеризу­ется тем, что расположение целевых вершин или их близость не влияют на порядок раскрытия. Существует несколько алгоритмов слепого перебора. Рассмотрим три наиболее типичных: алгоритм полного перебора, алго­ритм равных цен, алгоритм перебора в глубину.

Алгоритм полного перебора. Вершины раскрываются в том порядке, в котором они были порождены. Первой раскрывается начальная вершина. Проверяется, нет ли среди порожденных вершин целевой. Если есть, то поиск заканчивается. Если нет, то раскрывается первая из порожденных вершин и проверяется наличие целевых

76

вершин. Затем раскрывается вторая из порожденных вершин и т. д.

Для структуризованной записи алгоритмов поиска в пространстве состояний введем понятия списков откры­тых (ОТК) и закрытых (ЗКР) вершин. Список закры­тых вершин — это список, где размещаются идентифика­торы раскрытых вершин и идентификатор вершины, которую предстоит раскрыть в данный момент. Вершины из списка ЗКР, кроме последней, раскрывать нельзя. Список открытых вершин — это список, где размещаются вершины, которые могут и должны быть раскрыты. Стратегии поиска различаются правилами размещения вершин в списке ОТК и выбора очередной вершины для раскрытия.

В структуризованном виде алгоритм полного перебо­ра можно представить следующим образом.

1. Поместить начальную вершину в список ОТК.

2. Если список ОТК пуст, то подать сигнал о неудаче поиска, в ином случае перейти к следующему шагу.

3. Взять первую вершину из списка ОТК и перенести ее в список ЗКР; присвоить вершине идентификатор v.

4. Раскрыть вершину v. Поместить все дочерние не­ повторяющиеся (т. е. не встречающиеся в списке ЗКР) вершины в конец списка ОТК и построить указатели, ведущие от них к вершине v. Если вершина v не имеет дочерних вершин или имеет только повторяющиеся до­ черние вершины, то перейти к шагу 2.

5. Проверить, не является ли одна из дочерних вершин v целевой. Если является, то выдать решение; в ином случае перейти к шагу 2.

В этом алгоритме предполагается, что начальная вершина (корень) не может быть целевой. Алгоритм, безусловно, позволяет найти оптимальное (минимальное по числу дуг) решение. Например, использование этого алгоритма для решения задачи о выборе маршрута (с минимальным расстоянием) по существу сводится к построению графа состояний (см. рис. 3.4). Имея этот граф и сравнивая расстояния различных маршрутов, ведущих к целевым состояниям, можно выбрать опти­мальные маршруты. Как следует из графа состояний, таких маршрутов два — маршруты, ведущие к целевым состояниям ABCDA и ADCBA.

Алгоритм равных цен. Пусть каждой дуге поставле-на в соответствие некоторая функция стоимости сij, требуется найти путь минимальной стоимости, Раскры-

77

тие вершин осуществляется в порядке возрастания их стоимости. Обозначим g(v) — стоимость раскрытия не­которой вершины v и опишем алгоритм равных цен.

1. Поместить начальную вершину s0 в список ОТК. Положить g(so) =0.

2. Если список ОТК пуст, то подать сигнал о неудаче поиска; в ином случае перейти к следующему шагу.

3. Взять из списка ОТК ту вершину, для которой величина g(v) имеет наименьшее значение, и поместить ее в список ЗКР. Присвоить этой вершине идентифика­ тор v (если вершин с минимальной стоимостью не­ сколько, то можно выбрать любую из них).

4. Если v есть целевая вершина, то выдать решающий путь; в ином случае перейти к следующему шагу.

5. Раскрыть вершину v. Для каждой дочерней вер­ шины vi вычислить стоимость g(vi) по формуле g(vi) = =g(v)+c(v,vi)- Поместить эти вершины вместе с соот­ ветствующими им g(vi) в список ОТК и построить указатели, идущие от них к вершине v. Если вершина v не имеет дочерних вершин, то сразу перейти к шагу 2.

6. Перейти к шагу 2.

Алгоритм равных цен является обобщением алгорит­ма полного перебора и сводится к нему при условии, что стоимости раскрытия всех вершин равны. При при­менении этого алгоритма для решения задачи о выборе маршрута раскрывается меньшее число вершин. Граф решения приведен на рис. 3.5, где на дугах указаны «стоимости» с (v, vi), а на вершинах кроме обозначения состояния — значение функции g(vi), а также (в скоб­ках) порядковый номер, в котором раскрываются вер­шины.

Алгоритм перебора в глубину. Определим глубину вершины числом, равным номеру ее уровня. При методе перебора в глубину всегда раскрывается та из вершим, которая имеет наибольшую глубину. Так как несколько вершин могут иметь одинаковую наибольшую глубину, предполагается, что имеется правило выбора одной из них. Кроме того, обычно по тем или иным соображе­ниям задается граничная глубина; вершины, имеющие глубину, равную граничной, не раскрываются. Таким образом, метод перебора в глубину можно определить как метод перебора, при котором всегда раскрывается та из вершин, которая имеет наибольшую глубину, меньшую граничной.

Рис. 3.5. Граф решения задачи о выборе маршрута при использовании алгоритма равных иен

Рассмотрим алгоритм перебора в глубину в структу­ризованном виде.

1. Поместить начальную вершину в список ОТК-

2. Если список ОТК пуст, то выдается сообщение о неудаче, в ином случае перейти к шагу 3.

. Взять первую вершину из списка ОТК и перенести список ЗКР. Этой вершине присвоить идентификатор v. 4. Если глубина вершины v равна граничной глуби­не, то перейти к 2, в ином случае — к 5. 5. Раскрыть вершину v. Поместить все дочерние вершины в начало списка ОТК и построить указатели, идущие от них к вершине v. Если v не имеет дочерних вершин, то перейти к шагу 2.

6. Если одна из этих вершин целевая, то на выход 79

выдать решение, полу­чаемое путем просмотра назад в соответствии с указателями, в ином случае перейти к ша­гу 2.

Один из возможных графов решения задачи выбора маршрута с по­мощью алгоритма пере­бора в глубину приве­ден на рис. 3.6. При при­менении этого алгорит­ма решение зависит от стратегии упорядочения вершин в списке ОТК. В приведенном решении найден неоптимальный маршрут.