
- •Глава 2. Элементы векторной алгебры §2.1. Линейные операции над векторами
- •§2.2. Линейная зависимость векторов. Базис и координаты
- •10. Определение линейной зависимости и независимости векторов. Введем важные понятия, играющие большую роль в линейных уравнениях, например, – понятия линейной зависимости и независимости векторов
- •§2.3. Произведение векторов
- •2.3.1. Скалярное произведение векторов
- •2.3.2. Векторное произведение двух векторов
- •10. Определение векторного произведения. Его механический смысл.
- •2.3.3. Смешанное произведение трех векторов
2.3.3. Смешанное произведение трех векторов
10. Определение смешанного произведения. Введем определение.
Определение. Смешанным
произведением трех векторов![]() и
и![]() (обозначается символом
(обозначается символом![]() )
называется скалярное произведение
вектора
)
называется скалярное произведение
вектора![]() на вектор
на вектор![]() :
:
![]() =
=![]() .
(2.45)
.
(2.45)
Теорема. Модуль смешанного
произведения![]() равен объему параллелепипеда, построенного
на векторах
равен объему параллелепипеда, построенного
на векторах![]() и
и![]() .
.
Доказательство. Пусть
векторы![]() и
и![]() ,
образующие правую тройку, некомпланарны
(в случае их компланарности
,
образующие правую тройку, некомпланарны
(в случае их компланарности![]() =
=![]() =0
– равенство очевидно).
=0
– равенство очевидно).
Тогда (рис.2.19)
![]() =
=![]()
![]() – смешанное произведение векторов
– смешанное произведение векторов![]() и
и![]() равно объему параллелепипеда, построенного
на этих векторах.
равно объему параллелепипеда, построенного
на этих векторах.
Для случая левой ориентации
тройки векторов
![]() и
и![]() угол между векторами
угол между векторами![]() и
и![]() тупой; в таком случае произведение
тупой; в таком случае произведение![]() =
–V(ориентация
пространства всюду предполагается
правой).
=
–V(ориентация
пространства всюду предполагается
правой).
20. Свойства смешанного произведения.
1) смешанное произведение равно нулю тогда и только тогда, когда все три вектора компланарны (в доказательстве можно использовать геометрический смысл смешанного произведения);
2)
![]() – смешанное произведение не зависит
от группировки множителей.
– смешанное произведение не зависит
от группировки множителей.
Доказательство. Оба смешанных
произведения имеют одинаковые абсолютные
величины, ибо равны объему параллелепипеда,
построенного на векторах![]() и
и![]() .
Знаки произведений также совпадают,
ибо если тройка
.
Знаки произведений также совпадают,
ибо если тройка![]() ,
,![]() – правая, то и
– правая, то и![]() – правая тройка. Аналогично при левой
ориентации тройки векторов.
– правая тройка. Аналогично при левой
ориентации тройки векторов.
3) законы круговой и парной
перестановки векторов:
![]() =
=![]() =
=![]() =
=![]() =
=
=
=![]() =
=![]() – доказательства очевидны;
– доказательства очевидны;
4)
![]() – смешанное произведение векторов
обладает распределительным свойством;
это следует из распределительного
свойства скалярного произведения;
– смешанное произведение векторов
обладает распределительным свойством;
это следует из распределительного
свойства скалярного произведения;
5)
![]() – скалярный множитель можно выносить
за знак смешанного произведения (это
есть следствие соответствующих законов
для векторного и скалярного произведений).
– скалярный множитель можно выносить
за знак смешанного произведения (это
есть следствие соответствующих законов
для векторного и скалярного произведений).
30. Смешанное
произведение в координатной форме.
Пусть заданы разложения векторов![]() ,
,![]() и
и![]() .
Найдем выражение для смешанного
произведения их.
.
Найдем выражение для смешанного
произведения их.
Векторное произведение
![]()
![]()
![]() =
=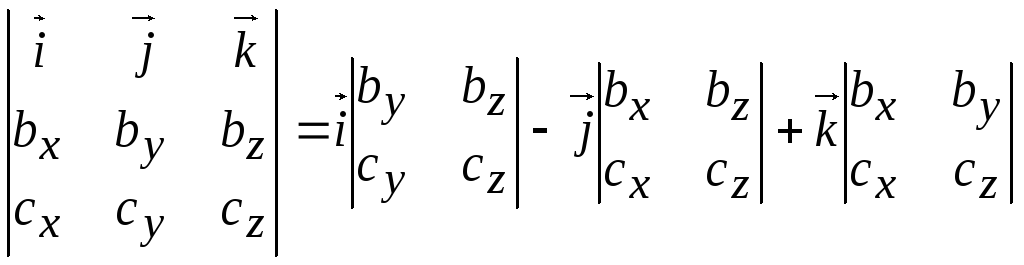
и, следовательно, смешанное произведение
![]() =
=![]() =
=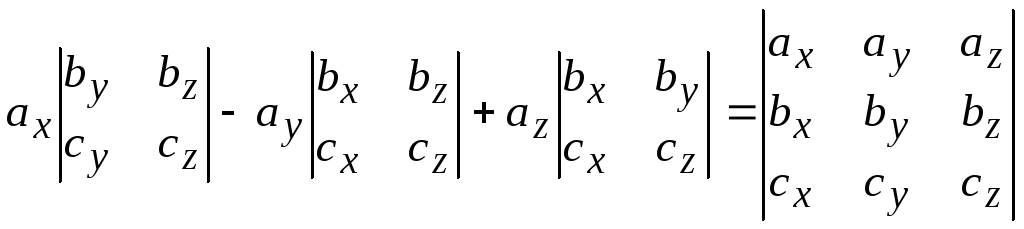 .
(2.46)
.
(2.46)
Пример. Доказать, что точки![]() и
и![]() лежат в одной плоскости.
лежат в одной плоскости.
Решение. «Построим» три
вектора![]() и
и![]() :
четыре точки лежат в одной плоскости,
если эти три вектора компланарны. Имеем:
:
четыре точки лежат в одной плоскости,
если эти три вектора компланарны. Имеем:![]() ,
,![]() =
=![]() ,
,![]() =
=![]() .
.
По формуле (2.46) составим смешанное произведение
![]()
![]()
![]() =
=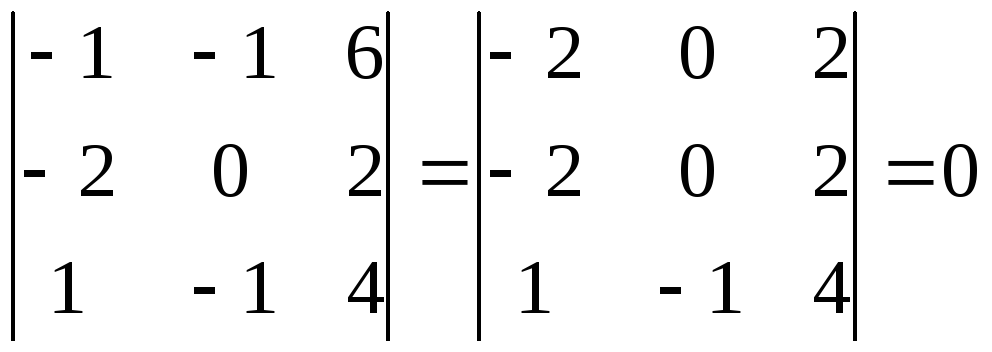
– векторы компланарны и, следовательно, заданные четыре точки лежат в одной плоскости.
Этим завершим изложение основ векторной алгебры.
