2.3.2. Векторное произведение двух векторов

Во многих вопросах механики и электротехники большую роль играет понятие векторного произведения двух векторов. Введем это понятие.

10. Определение векторного произведения. Его механический смысл.

Определение. Векторным произведением векторана векторназывается вектор(для обозначения употребляют символы==ab=), удовлетворяющий следующим трем условиям (рис.2.16 хх ):

а) вектор ортогонален каждому из перемножаемых векторов:│ и │;

б) вектор направлен так, что тройка векторовявляется правой, то есть он направлен в ту сторону, откуда поворот от первого вектора произведения (вектора) ко второму () виден против часовой стрелки;

в) модуль произведения (– угол между векторамии)

. (2.41)

Установим механический смысл векторного произведения векторов.

а) пусть вектор есть сила, приложенная к некоторой точкеM,– радиус-вектор точкиM. Тогда векторное произведениеопределяет моментсилыотносительно точкиO.

б) пусть (рис.2.17) имеем твердое тело, вращающееся вокруг оси OO’, векторобозначает скорость некоторой точкиMэтого тела,– угловая скорость вращения тела. Тогда скорость точкиMможно представить формулой:=, где– радиус-вектор точкиM.

2⁰. Свойства векторного произведения. Приведем свойства векторного произведения.

1) необходимым и достаточным условием коллинеарности векторов иявляется равенство нулю их векторного произведения:

, (2.42)

иначе (2.42) называется условием коллинеарности векторов ив векторной форме. Приведем доказательство.

Необходимость. Пусть векторыиколлинеарны; докажем, что тогда выполняется условие (2.42).

В случае коллинеарности векторов иугол между ними равен либо нулю, либо. В таком случае модуль произведения ,откуда произведение=0.

Достаточность. Пусть выполнено условие (2.42). Докажем коллинеарность векторови.

Равенство нулю векторного произведения равносильно равенству нулю его модуля: , что равносильно тому, что либо=0, либо=0, либо уголили. Завершить доказательство можно тем, что нулевой вектор коллинеарен с любым вектором.

2) модуль векторного произведения равен площади параллелограмма, построенного на векторах и(этот факт выражает геометрический смысл формулы (2.41)):

. (2.43)

Доказательство. Модуль (рис.2.18)==.

3) =0 – следует из свойства 1;

4) = –– векторное произведение векторов антикоммутативно (доказательство см. п.2 определения векторного произведения);

5) – скалярный множитель можно выносить за знак векторного произведения (ибо если одну из сторон параллелограмма удлинить враз, то и площадь увеличится враз);

6) – векторное произведение векторов обладает дистрибутивным свойством сложения относительно умножения векторов (доказательство опустим).

Замечание. Векторное произведение не обладает сочетательным (ассоциативным) свойством: произведениене обязательно равно.

Приведенные выше свойства дают возможность раскрывать скобки в выражениях, включающих векторное произведение векторов. Приведем пример.

Пример..

3⁰. Векторное произведение в декартовых координатах. Составим всевозможные векторные произведения из ортов; нетрудно проверить, что

.

Для векторов инайдем:

==

==

=.

Если учесть, что коэффициенты при ортах суть определители ,,,то полученный результат можно записать в виде символического определителя:

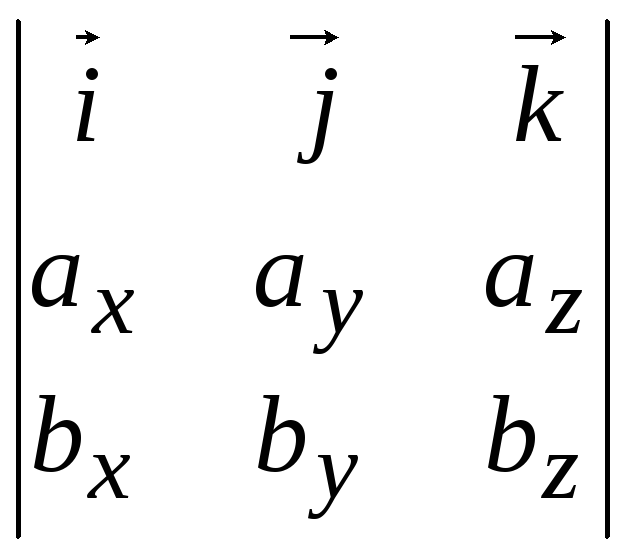=, (2.44)

при условии его раскрытия по элементам первой строки (ортам ).

Пример.Найти а) векторное произведение векторови; б) определить площадь параллелограмма, построенного на этих векторах; найти орт, нормальный заданным векторам и записать с его помощью векторное произведение.

Решение. а) имеем по формуле (2.44)

=.

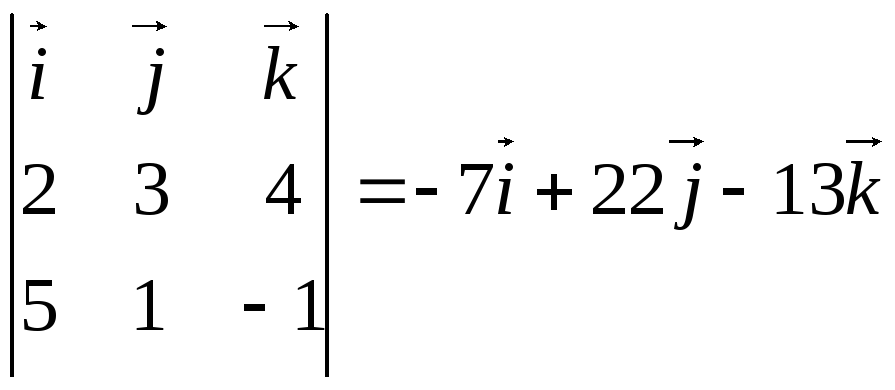б) найдем по формуле (2.43) площадь параллелограмма, построенного на векторах и:. в) орт векторного произведения(обозначим его) определяется соотношением:

=.

Векторное произведение =