§2.2. Линейная зависимость векторов. Базис и координаты

10. Определение линейной зависимости и независимости векторов. Введем важные понятия, играющие большую роль в линейных уравнениях, например, – понятия линейной зависимости и независимости векторов

Определение 1. Линейной комбинацией векторовназывается сумма произведений этих векторов на скаляры:

. (2.8)

Определение 2. Система векторовназывается линейно зависимой системой, если линейная комбинация их (2.8) обращается в нуль:

=0, (2.9)

причем среди чиселсуществует хотя бы одно, отличное от нуля.

Определение 3. Векторыназываются линейно независимыми, если их линейная комбинация (2.8) обращается в нуль лишь в случае, когда все числа.

Из этих определений можно получить следующие следствия.

Следствие 1. В линейно зависимой системе векторов хотя бы один вектор может быть выражен как линейная комбинация остальных.

Доказательство. Пусть выполнено (2.9) и пусть для определенности, коэффициент. Имеем тогда:. Заметим, что справедливо и обратное утверждение.

Следствие 2. Если система векторовсодержит нулевой вектор, то эта система (обязательно) линейно зависима – доказательство очевидно.

Следствие 3. Если средиnвекторовкакие либоk() векторов линейно зависимы, то и всеnвекторов линейно зависимы (опустим доказательство).

2⁰. Линейные комбинации двух, трех и четырех векторов. Рассмотрим вопросы линейной зависимости и независимости векторов на прямой, плоскости и в пространстве. Приведем соответствующие теоремы.

Теорема 1. Для того чтобы два вектора были линейно зависимы, необходимо и достаточно, чтобы они были коллинеарны.

Необходимость. Пусть векторыилинейно зависимы. Это означает, что их линейная комбинация=0 и (ради определенности). Отсюда следует равенство, и (по определению умножения вектора на число) векторыиколлинеарны.

Достаточность. Пусть векторыиколлинеарны (║) (предполагаем, что они отличны от нулевого вектора; иначе их линейная зависимость очевидна).

По теореме (2.7) (см. §2.1,п.2⁰) тогдатакое, что, или– линейная комбинация равна нулю, причем коэффициент приравен 1 – векторыилинейно зависимы.

Из этой теоремы вытекает следующее следствие.

Следствие. Если векторыине коллинеарны, то они линейно независимы.

Теорема 2. Для того чтобы три вектора были линейно зависимы, необходимо и достаточно, чтобы они были компланарны.

Необходимость. Пусть векторы,илинейно зависимы. Покажем, что они компланарны.

Из определения линейной зависимости векторов следует существование чисел итаких, что линейная комбинация, и при этом (для определенности). Тогда из этого равенства можно выразить вектор:=, то есть векторравен диагонали параллелограмма, построенного на векторах, стоящих в правой части этого равенства (рис.2.6). Это означает, что векторы,илежат в одной плоскости.

Достаточность. Пусть векторы,икомпланарны. Покажем, что они линейно зависимы.

Исключим случай коллинеарности какой либо пары векторов (ибо тогда эта пара линейно зависима и по следствию 3 (см.п.1⁰) все три вектора линейно зависимы). Заметим, что такое предположение исключает также существование нулевого вектора среди указанных трех.

Перенесем три компланарных вектора в одну плоскость и приведем их к общему началу. Через конец вектора проведем прямые, параллельные векторами; получим при этом векторыи(рис.2.7) – их существование обеспечено тем, что векторыине коллинеарные по предположению векторы. Отсюда следует, что вектор=+. Переписав это равенство в виде (–1)++=0, заключаем, что векторы,илинейно зависимы.

Из доказанной теоремы вытекает два следствия.

Следствие 1. Пустьине коллинеарные векторы, вектор– произвольный, лежащий в плоскости, определяемой векторамии, вектор. Существуют тогда числаитакие, что

=+. (2.10)

Следствие 2. Если векторы,ине компланарны, то они линейно независимы.

Теорема 3. Любые четыре вектора линейно зависимы.

Доказательство опустим; с некоторыми изменениями оно копирует доказательство теоремы 2. Приведем следствие из этой теоремы.

Следствие. Для любых некомпланарных векторов,,и любого вектораитакие, что

. (2.11)

Замечание. Для векторов в (трехмерном) пространстве понятия линейной зависимости и независимости имеют, как это следует из приведенных выше теорем 1-3, простой геометрический смысл.

Пусть имеются два линейно зависимых вектора и. В таком случае один из них является линейной комбинацией второго, то есть просто отличается от него численным множителем (например,). Геометрически это означает, что оба вектора находятся на общей прямой; они могут иметь одинаковое или противоположное направления (рис.2.8 хх ).

Если же два вектора расположены под углом друг к другу (рис.2.9 хх ), то в этом случае нельзя получить один из них умножением другого на число – такие векторы линейно независимы. Следовательно, линейная независимость двух векторов иозначает, что эти векторы не могут быть уложены на одну прямую.

Выясним геометрический смысл линейной зависимости и независимости трех векторов.

Пусть векторы ,илинейно зависимы и пусть (для определенности) векторявляется линейной комбинацией векторови, то есть расположен в плоскости, содержащей векторыи. Это означает, что векторы,илежат в одной плоскости. Справедливо и обратное утверждение: если векторы,илежат в одной плоскости, то они линейно зависимы.

Таким образом, векторы ,илинейно независимы в том и только в том случае, если они не лежат в одной плоскости.

3⁰. Понятие базиса. Одним из важнейших понятий линейной и векторной алгебры является понятие базиса. Введем определения.

Определение 1. Пара векторов называется упорядоченной, если указано, какой вектор этой пары считается первым, а какой вторым.

Определение 2. Упорядоченная пара,неколлинеарных векторов называется базисом на плоскости, определяемой заданными векторами.

Теорема 1. Всякий векторна плоскости может быть представлен как линейная комбинация базисной системы векторов,:

(2.12)

и это представление единственно.

Доказательство. Пусть векторыиобразуют базис. Тогда любой векторможно представить в виде.

Для доказательства единственности предположим, что имеется еще одно разложение . Имеем тогда=0, причем хотя бы одна из разностей отлична от нуля. Последнее означает, что векторыилинейно зависимы, то есть коллинеарны; это противоречит утверждению, что они образуют базис.

Но тогда – разложение единственно.

Определение 3. Тройка векторов называется упорядоченной, если указано, какой вектор ее считается первым, какой вторым, а какой третьим.

Определение 4. Упорядоченная тройка некомпланарных векторов называется базисом в пространстве.

Здесь также справедлива теорема разложения и единственности.

Теорема 2. Любой векторможет быть представлен как линейная комбинация базисной системы векторов,,:

(2.13)

и это представление единственно (опустим доказательство теоремы).

В разложениях (2.12) и (2.13) величины называются координатами векторав заданном базисе (точнее, аффинными координатами).

При фиксированном базисе иможно писать.

Например, если задан базис и дано, что, то это означает, что имеет место представление (разложение).

4⁰. Линейные операции над векторами в координатной форме. Введение базиса позволяет линейные операции над векторами заменить обычными линейными операциями над числами – координатами этих векторов.

Пусть задан некоторый базис . Очевидно, задание координат вектора в этом базисе полностью определяет сам вектор. Имеют место следующие предложения:

а) два вектора иравны тогда и только тогда, когда равны их соответственные координаты:

; (2.14)

б) при умножении вектора на числоего координаты умножаются на это число:

; (2.15)

в) при сложении векторов складываются их соответственные координаты:

. (2.16)

Доказательства этих свойств опустим; докажем лишь для примера свойство б). Имеем

==

==.

Замечание. В пространстве (на плоскости) можно выбрать бесконечно много базисов.

Приведем пример перехода от одного базиса к другому, установим соотношения между координатами вектора в различных базисах.

Пример 1. В базисной системезаданы три вектора:,и. В базисе,,векторимеет разложение. Найти координаты векторав базисе.

Решение. Имеем разложения:,,; следовательно,=+2+= =, то естьв базисе.

Пример 2. Пусть в некотором базисечетыре вектора заданы своими координатами:,,и.

Выяснить, образуют ли векторы базис; в случае положительного ответа найти разложение векторав этом базисе.

Решение. 1) векторы образуют базис, если они линейно независимы. Составим линейную комбинацию векторов() и выясним, при какихиона обращается в нуль:=0. Имеем:

=++=

=.

По определению равенства векторов в координатной форме получим следующую систему (линейных однородных алгебраических) уравнений: ;;, определитель которой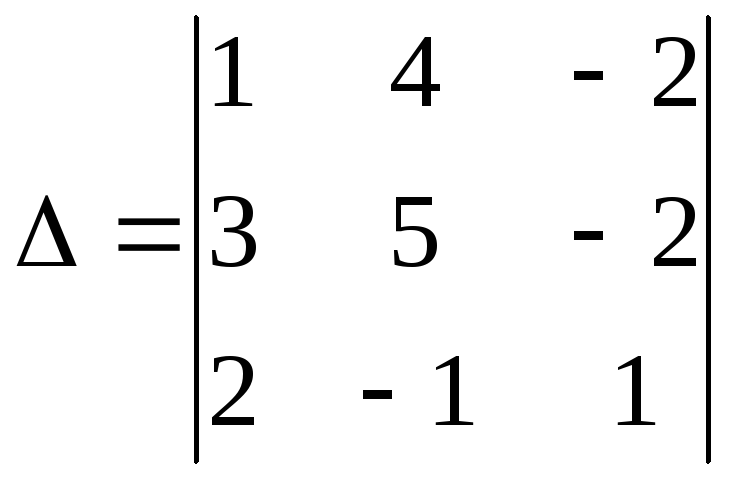=1, то есть система имеет (лишь) тривиальное решение. Это означает линейную независимость векторови, следовательно, они образуют базис.

2) разложим вектор в этом базисе. Имеем:=или в координатной форме.

Переходя к равенству векторов в координатной форме, получим систему линейных неоднородных алгебраических уравнений: ;;. Решая ее (например, по правилу Крамера), получим:,,и (). Имеем разложение векторав базисе:=.

5⁰. Проекция вектора на ось. Свойства проекций. Пусть имеется некоторая осьl, то есть прямая с выбранным на ней направлением и пусть задан некоторый вектор.Определим понятие проекции векторана осьl.

Определение. Проекцией векторана осьlназывается произведение модуля этого вектора на косинус угла между осьюlи вектором (рис.2.10):

. (2.17)

Следствием этого определения является утверждение о том, что равные векторы имеют равные проекции (на одну и ту же ось).

Отметим свойства проекций.

1) проекция суммы векторов на некоторую ось lравна сумме проекций слагаемых векторов на ту же ось:

. (2.18)

2) проекция произведения скаляра на вектор равна произведению этого скаляра на проекцию вектора на ту же ось:

=. (2.19)

Следствие. Проекция линейной комбинации векторов на ось равна линейной комбинации их проекций:

. (2.20)

Доказательства свойств опустим.

6⁰. Прямоугольная декартова система координат в пространстве.Разложение вектора по ортам осей. Пусть в качестве базиса выбраны три взаимно перпендикулярных орта; для них вводим специальные обозначения. Поместив их начала в точкуO, направим по ним (в соответствии с ортами) координатные осиOx,OyиOz(ось с выбранным на ней положительным направлением, началом отсчета и единицей длины называется координатной осью).

Определение. Упорядоченная система трех взаимно перпендикулярных координатных осей с общим началом и общей единицей длины называется прямоугольной декартовой системой координат в пространстве.

Ось Ox называется осью абсцисс,Oy– осью ординат иOz – осью аппликат.

Займемся разложением произвольного вектора по базису . Из теоремы (см.§2.2,п.3⁰, (2.13)) следует, чтоможет быть и единственным образом разложен по базису(здесь вместо обозначения координатупотребляют):

. (2.21)

В (2.21) суть (декартовы прямоугольные) координаты вектора. Смысл декартовых координат устанавливает следующая теорема.

Теорема. Декартовы прямоугольные координатывектораявляются проекциями этого вектора соответственно на осиOx,OyиOz.

Доказательство.Поместим векторв начало системы координат – точкуO. Тогда его конец будет совпадать с некоторой точкой.

Проведем через точку три плоскости, параллельные координатным плоскостямOyz,OxzиOxy(рис.2.11 хх ). Получим тогда:

. (2.22)

В (2.22) векторы и называются составляющими векторапо осямOx,OyиOz.

Пусть через иобозначены соответственно углы, образованные векторомс ортами. Тогда для составляющих получим следующие формулы:

==, ==, ==(2.23)

Из (2.21), (2.22) (2.23) находим:

==;==;==(2.23)

– координаты вектораесть проекции этого вектора на координатные осиOx,OyиOzсоответственно.

Замечание . Числаназываются направляющими косинусами вектора.

Модуль вектора (диагональ прямоугольного параллелепипеда) вычисляется по формуле:

. (2.24)

Из формул (2.23) и (2.24) следует, что направляющие косинусы могут быть вычислены по формулам:

=;=;=. (2.25)

Возводя обе части каждого из равенств в (2.25) и складывая почленно левые и правые части полученных равенств, придем к формуле:

(2.26)

– не любые три угла образуют некоторое направление в пространстве, но лишь те, косинусы которых связаны соотношением (2.26).

7⁰. Радиус-вектор и координаты точки.Определение вектора по его началу и концу. Введем определение.

Определение. Радиусом-вектором (обозначается) называется вектор, соединяющий начало координатOс этой точкой (рис.2.12 хх ):

. (2.27)

Любой точке пространства соответствует определенный радиус-вектор (и обратно). Таким образом, точки пространства представляются в векторной алгебре их радиус-векторами.

Очевидно, координаты точкиMявляются проекциями ее радиус-векторана координатные оси:

(2.28’)

и, таким образом,

(2.28)

– радиус-вектор точки есть вектор, проекции которого на оси координат равны координатам этой точки. Отсюда следует две записи: и.

Получим формулы для вычисления проекций вектора по координатам его начала – точкеи конца – точке.

Проведем радиус-векторы и вектор(рис.2.13). Получим, что

==(2.29)

– проекции вектора на координатные орты равны разностям соответствующих координат конца и начала вектора.

8⁰. Некоторые задачи на декартовы координаты.

1) условия коллинеарности векторов. Из теоремы (см.§2.1,п.2⁰, формула (2.7)) следует, что для коллинеарности векторовинеобходимо и достаточно, чтобы выполнялось соотношение:=. Из этого векторного равенства получаем три в координатной форме равенства:, откуда следует условие коллинеарности векторов в координатной форме:

(2.30)

– для коллинеарности векторов инеобходимо и достаточно, чтобы их соответствующие координаты были пропорциональны.

2) расстояние между точками. Из представления (2.29) следует, что расстояниемежду точкамииопределяется формулой

==. (2.31)

3) деление отрезка в данном отношении. Пусть даны точкиии отношение. Нужно найти– координаты точкиM (рис.2.14).

Имеем из условия коллинеарности векторов: , откудаи

. (2.32)

Из (2.32) получим в координатной форме:

. (2.32’)

Из формул (2.32’) можно получить формулы для вычисления координат середины отрезка , полагая:

. (2.32”)

Замечание. Будем считать отрезкииположительными или отрицательными в зависимости от того, совпадает их направление с направлением от началаотрезка к концу, или не совпадает. Тогда по формулам (2.32) – (2.32”) можно находить координат точки, делящей отрезоквнешним образом, то есть так, что делящая точкаMнаходится на продолжении отрезка, а не внутри его. При этом конечно,.

4) уравнение сферической поверхности. Составим уравнение сферической поверхности – геометрического места точек, равноудаленных на расстояниеот некоторого фиксированного центра – точки. Очевидно, что в данном случаеи с учетом формулы (2.31)

. (2.33)

Уравнение (2.33) и есть уравнение искомой сферической поверхности.