3. Упрощение логических выражений
Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определённому виду путем использования основных законов алгебры логики.
Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определённому виду путем использования основных законов алгебры логики.
Покажем на примерах некоторые приемы и способы, применяемые при упрощении логических формул:
1)
(законы алгебры логики применяются в следующей последовательности: правило де Моргана, сочетательный закон, правило операций переменной с её инверсией и правило операций с константами);
2
)
(применяется правило де Моргана, выносится за скобки общий множитель, используется правило операций переменной с её инверсией);
3)
(повторяется второй сомножитель, что разрешено законом идемпотенции; затем комбинируются два первых и два последних сомножителя и используется закон склеивания)
4)
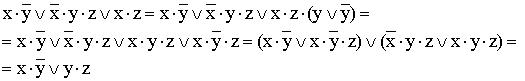
(вводится
вспомогательный логический сомножитель
(
);
затем комбинируются два крайних и два
средних логических слагаемых и
используется закон поглощения);
5
)
(сначала добиваемся, чтобы знак отрицания стоял только перед отдельными переменными, а не перед их комбинациями, для этого дважды применяем правило де Моргана; затем используем закон двойного отрицания);
6)
(выносятся за скобки общие множители; применяется правило операций с константами);
7)
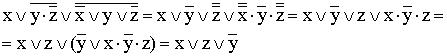
(к отрицаниям неэлементарных формул применяется правило де Моргана; используются законы двойного отрицания и склеивания);
8)
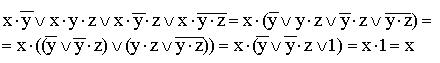
(общий
множитель x выносится за скобки,
комбинируются слагаемые в скобках —
первое с третьим и второе с четвертым,
к дизъюнкции
применяется
правило операции переменной с её
инверсией);
9)
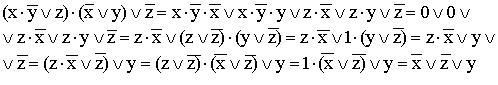
(используются распределительный закон для дизъюнкции, правило операции переменной с ее инверсией, правило операций с константами, переместительный закон и распределительный закон для конъюнкции);
10)
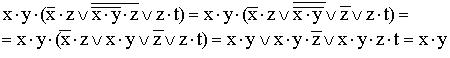
(используются правило де Моргана, закон двойного отрицания и закон поглощения).
Задание №1. Решить задачи, согласно варианту, заданному преподавателем. Решения предоставить:
Для п.1 в виде таблиц истинности, в которой значения всех столбцов, кроме первых трех, должны быть вычислены с применением соответствующих формул, составленных в MS Excel.
Для п.2 в виде двух таблиц истинности, в которых значения последнего столбца должны быть вычислены с применением соответствующих формул, составленных в MS Excel. Итоговая таблица должна содержать результаты сравнения последних столбцов таблиц истинности и вывод о равносильности высказываний.
Для п.3 предоставить всю цепочку упрощений предложенных выражений с использованием редактора формул.
|
Вариант 1. |
Вариант 2. | ||||||||||||
|
1. Постройте таблицу истинности для следующего логического выражения:
|
1. Постройте таблицу истинности для следующего логического выражения:
| ||||||||||||
|
2. Установить, равносильны ли два высказывания:
|
2. Установить, равносильны ли два высказывания:
| ||||||||||||
|
3. Упростить логические выражения:
а)
б)
|
3. Упростить логические выражения:
а)
б)
| ||||||||||||
|
Вариант 3. |
Вариант 4. | ||||||||||||
|
1. Постройте таблицу истинности для следующего логического выражения:
|
1. Постройте таблицу истинности для следующего логического выражения:
| ||||||||||||
|
2. Установить, равносильны ли два высказывания:
|
2. Установить, равносильны ли два высказывания:
| ||||||||||||
|
3. Упростить логические выражения:
а)
б)
|
3. Упростить логические выражения:
а)
б)
| ||||||||||||
|
Вариант 5. |
Вариант 6. | ||||||||||||
|
1. Постройте таблицу истинности для следующего логического выражения:
|
1. Постройте таблицу истинности для следующего логического выражения:
| ||||||||||||
|
2. Установить, равносильны ли два высказывания:
|
2. Установить, равносильны ли два высказывания:
| ||||||||||||
|
3. Упростить логические выражения:
а)
б)
|
3. Упростить логические выражения:
а)
б)
| ||||||||||||
|
Вариант 7. |
Вариант 8. | ||||||||||||
|
1. Постройте таблицу истинности для следующего логического выражения:
|
1. Постройте таблицу истинности для следующего логического выражения:
| ||||||||||||
|
2. Установить, равносильны ли два высказывания:
|
2. Установить, равносильны ли два высказывания:
| ||||||||||||
|
3. Упростить логические выражения:
а)
б)
|
3. Упростить логические выражения:
а)
б)
| ||||||||||||
|
Вариант 9. |
Вариант 10. | ||||||||||||
|
1. Постройте таблицу истинности для следующего логического выражения:
|
1. Постройте таблицу истинности для следующего логического выражения:
| ||||||||||||
|
2. Установить, равносильны ли два высказывания:
|
2. Установить, равносильны ли два высказывания:
| ||||||||||||
|
3. Упростить логические выражения:
а)
б)
|
3. Упростить логические выражения:
а)
б)
| ||||||||||||
|
Вариант 11 |
Вариант 12 | ||||||||||||
|
1. Постройте таблицу истинности для следующего логического выражения:
|
1. Постройте таблицу истинности для следующего логического выражения:
| ||||||||||||
|
2. Установить, равносильны ли два высказывания:
|
2. Установить, равносильны ли два высказывания:
| ||||||||||||
|
3. Вычислите значение логического выражения: A B C 1 0 1
|
3. Вычислите значение логического выражения: A B C 0 1 0 | ||||||||||||
|
4. Упростите выражение
|
4. Упростите выражение
| ||||||||||||
|
Вариант 13 |
Вариант 14 | ||||||||||||
|
1. Постройте таблицу истинности для следующего логического выражения:
|
1. Постройте таблицу истинности для следующего логического выражения:
| ||||||||||||
|
2. Установить, равносильны ли два высказывания:
|
2. Установить, равносильны ли два высказывания:
| ||||||||||||
|
3. Вычислите значение логического выражения: A B C 1 1 1
|
3. Вычислите значение логического выражения: A B C 0 0 1 | ||||||||||||
|
4. Упростите выражение
|
4. Упростите выражение
| ||||||||||||
|
Вариант 15 |
Вариант 16 | ||||||||||||
|
1. Постройте таблицу истинности для следующего логического выражения:
|
1. Постройте таблицу истинности для следующего логического выражения:
| ||||||||||||
|
2. Установить, равносильны ли два
высказывания:
|
2. Установить, равносильны ли два высказывания:
| ||||||||||||
|
3. Вычислите значение логического выражения: A B C 1 0 1 |
3. Вычислите значение логического выражения: A B C 1 0 1 | ||||||||||||
|
4. Упростите выражение
|
4. Упростите выражение
|
и
и
и
и
и
и
и
и
и
и
и
и
и
и
и
и
