
- •Специальные главы физики
- •Практическая значимость курса
- •Основы теории вероятностей Вероятность случайного события
- •Характеристики случайной дискретной величины Среднее значение случайной величины
- •X1, x2, …, xk.
- •Свойства среднего
- •Основные определения
- •Относительная флуктуация
- •Характеристики случайНой непрерывНой величиНы
- •Биномиальное распределение
- •Распределение Пуассона
- •Условие нормировки
- •Среднее значение
- •Дисперсия
- •Пример 1
- •Пример 2
- •Пример 3
- •Пример 4
- •Пример 5
Распределение Пуассона
Пусть
вероятность появления признака у одной
частицы мала
![]() и общее число частиц велико
и общее число частиц велико
![]() ,
тогда, если
признак имеют в среднем
,
тогда, если
признак имеют в среднем
![]() частиц, то его вероятность дляn
частиц
частиц, то его вероятность дляn
частиц
 .
(1.18)
.
(1.18)
Результат получил Пуассон в 1837 г. на основе биномиального распределения.

Симеон Дени Пуассон (1781–1840)
Доказательство
Записываем биномиальное распределение (1.29)

 ,
,
где учтено
 .
.
При
![]() используем
используем
 ,
,
![]() ,
,
![]() ,
,
и получаем (1.18)
 .
.
Условие нормировки
Вычисляем сумму вероятностей всех возможных результатов
 .
.
При большом N используем
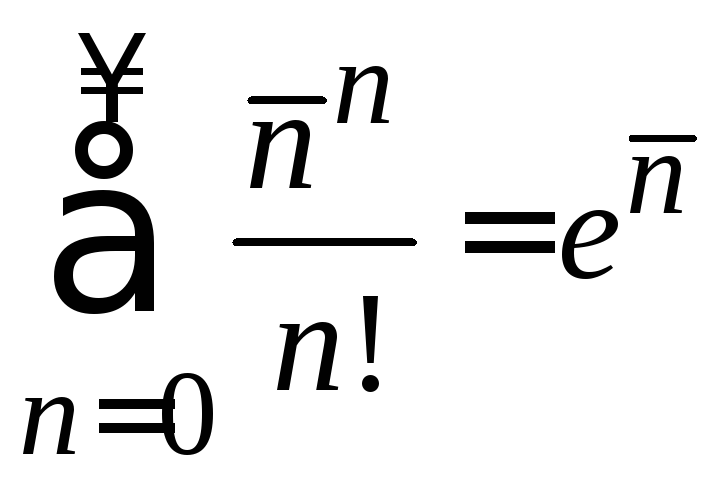 ,
,
получаем условие нормировки
 .
.
Среднеквадратичное число частиц и дисперсия
Используем результаты для биномиального распределения (1.28), (1.30) и (1.31)
![]() ,
,
![]() ,
,
![]() .
.
Для
распределения Пуассона учитываем
![]() и получаем среднеквадратичное число
частици
дисперсию
и получаем среднеквадратичное число
частици
дисперсию
![]() ,
(1.18а)
,
(1.18а)
![]() .
(1.18б)
.
(1.18б)
Частные и рекуррентные соотношения
Из (1.18)
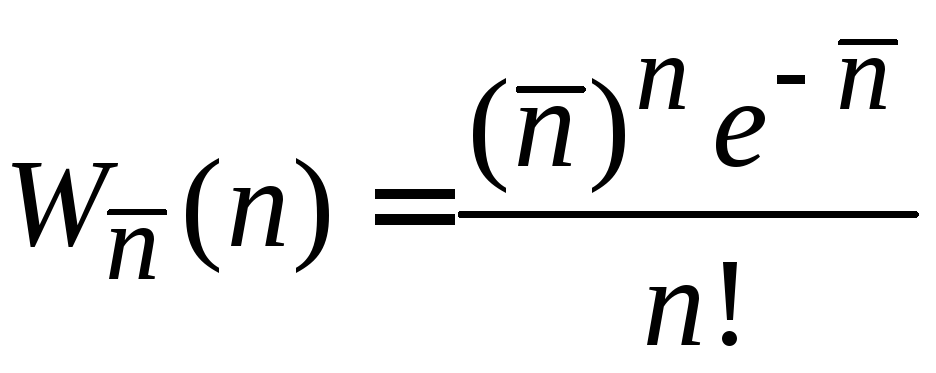
Прямой подстановкой находим
![]() ,
,
![]() ,
,
![]() ,
,
 .
(1.18в)
.
(1.18в)
График
распределения
для
![]() показан на рис. (б).
показан на рис. (б).

а б
Распределения
биномиальное (а) и Пуассона (б)для N
= 10,
![]() ,
р
= 0,45
,
р
= 0,45
Сравнение графиков показывает погрешность, допускаемую распределением Пуассона (график б), вызванную не достаточно малым p и не достаточно большим N.
нормальное распределение Гаусса
Если
признак имеется в среднем у
![]() частиц, причем выполняется
частиц, причем выполняется
![]() ,
то вероятность признака у n
частиц при относительно
малом отклонении от среднего
,
то вероятность признака у n
частиц при относительно
малом отклонении от среднего
![]() описывается нормальным
распределением
описывается нормальным
распределением
 .
(1.19)
.
(1.19)
Результат получил Гаусс в 1809 г.

Карл Фридрих Гаусс (1777–1855)
Доказательство
Условие
![]() означает
означает
![]() и выполнение
распределения Пуассона
и выполнение
распределения Пуассона
 .
.
Логарифмируем
![]() .
.
При
![]() используемформулу
Стирлинга
(рассматривается в курсе ММФ)
используемформулу
Стирлинга
(рассматривается в курсе ММФ)
 ,
,
которая дает
![]() .
.
Получаем
![]() .
.
Вводим
отклонение от среднего
![]() ,
тогда
,
тогда
 .
.
Для
распределения Гаусса учитываем ![]() .
Разлагаем
.
Разлагаем
![]() по степеням малой величины
по степеням малой величины![]() и сохраняем первые два слагаемые, считая
остальные несущественными:
и сохраняем первые два слагаемые, считая
остальные несущественными:

 .
.
Находим
 .
.
Потенцируем результат
и, используя
![]() ,заменяем
,заменяем ![]() ,
и получаем (1.19)
,
и получаем (1.19)
 .
.
Условие нормировки
На
основании ![]() считаем n
квазинепрерывным
и переходим от дискретного распределения
(1.19)
считаем n
квазинепрерывным
и переходим от дискретного распределения
(1.19)

к непрерывному распределению и получаем плотность вероятности
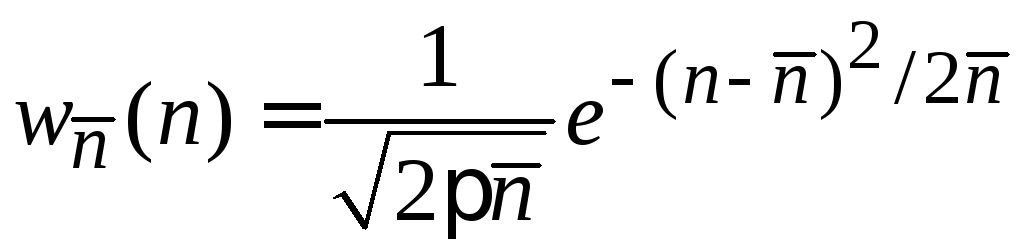 .
(1.19а)
.
(1.19а)
Условие нормировки имеет вид
 .
.
Верхний
предел интегрирования взят бесконечным,
поскольку функция
![]() быстро убывает при
быстро убывает при![]() .
Заменен аргумент
.
Заменен аргумент
![]() .
.
Нижний
предел
![]() при
при![]() равен
равен
![]() .
.
Верхний
предел
![]() дает
дает
![]() .
.
Последний интеграл является интегралом Пуассона
 .
.
В результате доказано, что плотность вероятности (1.19а) нормирована.
Среднее значение
В определение среднего случайной величины

подставляем
![]() .
Получаем
.
Получаем
 ,
,
где учтена нормировка
 ,
,
и среднее
отклонение от среднего
![]() .Следовательно,
в распределении Гаусса (1.19а)
.Следовательно,
в распределении Гаусса (1.19а)

величина
![]() является средним значением числа частицn.
является средним значением числа частицn.
