
готовые билеты по матану
.pdf1. Ограниченные, неограниченные множества.
Точные грани множества. Примеры..
Множество А называется ограниченным Сверху, если существует такое число M,
Что для всех X прин. А выполняетсяX<=M
Множество А называется ограниченным Снизу, если существует m,что для всех Х Из данного множества выполняется Х>=m.
Множество называется ограниченным,если Оно ограниченно и снизу и сверху m<=X,=M
Точная верхняя грань
supA=M
1.(Для всех Х прин. А): Х<=M
2.(Для всех Епсл.>0)(существует Х* прин. А):
Х*>M-Епсл.
Точная нижняя грань
Inf A=m
1.(Для всех Х прин. А):Х>=m
2.(для всех Епсл.>0)(Существует Х* прин. А):
Х*<m+Епсл,
Пример |
|
{1/3,1/9,1/27…} |
|
Sup A=1/3 |
1. X>0 |
Inf A=0 |
2. Для всех Епсл.>0 |
|
1\3^n < Епсл. |
3^n>1\Епсл. n>log3 1\Епсл. |
|
Епсл.=0.01 |
|
n>Log3 100 |
n=5 |
1\3^5 |
|
2. Последовательности. Точные пределы
последовательности. Корректность
определения предела. Примеры.
Понятие последовательности и её пределы.
Определение
Пусть каждому числу n натурального
ряда чисел
1,2…,n,… ставят в соотв число ,те заданы некоторые действительные числа, опред определённым образом
прономерованные, тогда мн-во вещественных чисел
|
наз числовой |
послед-ю{ } |
-члены |
послед-ти одно |
-общий член послед-ти |
Придел числовой последовательности
Число А называется приделом числовой последовательности, Если для любого положительного Епсл. найдется такой № зависящий от Епсл. начиная
с которого будет выпл. |Xn-A|<Епсл.
Числовая последовательность
Функция натурального аргумента называется Числовой последовательностью f(n)=Xn
3. Бесконечно малые и бесконечно большие последовательности.
Роль бесконечно малой последовательности в теории пределов. Примеры.
Последовательность Xn называется бесконечно малой, Если ее предел равен нулю.
Свойство Б.М.
1)Сумма Б.М.П. и есть Б.М.
2)Произведение 2х Б.М. ,есть произведение Б.М.
3)Произведение Б.М. последовательности,
на ограниченную Последовательность, есть Б.М.
Произведение любого конечного числа Б.М.П., есть Б.М.П.
Б.Б.П.
Последовательность Хn называется Б.Б.,если для любого Числа Е>0, найдется такой N(E) начиная с которого будет Выполняться неравенство Lin Xn= бесконечность.
4. Свойства последовательностей (3-4 из них с доказательством). Примеры.
Сумма 2х Б.М.П. и есть Б.М. 1/n+1/n^2=n+1/n^2
Произведение 2х Б.М. ,есть произведение Б.М. 1/n*1/n^2=1/n^3
Произведение Б.М. последовательности, на ограниченную
последовательность, есть Б.М.
1/n*(1/n+1)=1/n^2+1/n=n+1/n^2
Произведение любого конечного числа Б.М.П.,есть Б.М.П.
5. Свойства пределов последовательностей, связанные
с арифметическими операциями. Примеры.
1.Lim(Xn+Yn)=a+b т.е. Xn+Yn=a+b+jn, j-Б.М.
2.Lim CXn=C+A
Постоянную можно выносить за знак предела Имеем:

Xn=A+an an- б.м.
CXn=CA+Can Can = jn –б.м.
CXn=C*A+jn
3. Предел частного равен частному пределу, если b!=0
6. Монотонные последовательности. Предел монотонной последовательности. Пример.
Последовательность Xn называется М.
Возрастающая ,если каждый последующий член Больше предыдущего.{Xn=1,2…..}
Пример
Xn=1+1/2+…..+1/n
Xn+1=1+1/2+….+1/n+1/(n+1)
Xn+1 – Xn= 1/(n+1) >0
Xn+1 > Xn
Xn= 1*1/2 *1/3 *….*1/n
Xn+1/Xn= (1*1/2*1/3*…*1/n)/(1*1/2…1/n)=1/n+1<1
Теорема.
Пусть последовательность Xn М. и ограничена,
Тогда у нее существует придел.
7. Число е .
Число e выражается через предел следующим образом:
8. Принцип Кантора о вложенных отрезках.
Определение 1. Пусть даны две точки a и b, a 6 b.
Отрезком (сегментом или замкнутым числовым промежутком) назовем множество
[a, b] = {x R : a 6x 6 b}.
Определение 2. Пусть даны две точки a и b, a < b,
Интервалом (открытым числовым промежутком)
назовем множество (a, b) = {x R : a <x < b}.
Определение 3. Последовательность отрезков
I1 = [a1, b1], I2 = [a2, b2] , . . . ,
In = [an, bn] , . . . , называется вложенной, если выполнены включения In+1 In для
всех натуральных чисел n.
Промежутки называются вложенными, если В каждой последовательности содержится предыдущая
9. Подпоследовательность.Теорема Больцано-Вейерштрасса
Теорема. Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
Подпоследовательность {Xn}
Возьмем K1<K2<K3….
Xk1<Xk2<Xk3…. {Xkn} <-подпоследовательность
10. Фундаментальные последовательности.
Критерий Коши сходимости числовой последовательности. Пример.
Последовательность Xn называется фунд. Если для Всех Епсл.>0 и для всех натур. Чисел Р начина
С некоторого выполняется |Xn +p - Xn|<Епсл. Критерий Коши Для того,чтобы последовательности сходились
Необходимо и достаточно,что бы она была Фундаментальной.
Lim Xn=a
(для всех Епсл. >0)(Существует №(Епсл): (Для всех n>=N ))
|Xn-a|=Епсл. Рассмотрим
|Xn+p - Xn|=|Xn+p –a –(Xn-a)|<=|Xn+p-a|+|Xn-a|<Епсл.\2
+
+ Епсл\2 =Епсл. Пример
Xn=1+1/2+1/3+….+1/n
|Xn+p - Xn|=1/(n+1)+1/(n+2)+…+1/(n+p)>p/(n+p)=n/2n=1/2
11. Верхний и нижний пределы последовательности.
Теорема существования.
Нижний – это точная нижняя грань множества, Частичных приделов последовательности.
Верхний- это точная верхняя грань множества Частичных пределов последовательности. Частичный предел некоторой пос-ти- это Предел одной из ее подпоследовательностей, Если только он существует.
13. Точка сгущения множества. Примеры.
Точка сгущения – это, все равно что предельная точка.
Точка Р называется предельной точкой множества М, если для всей окрестности точки Р имеется, По крайней мере, еще одна точка множества М, кроме точки Р.
14. Определения предела функции по Гейне и Коши. Эквивалентность определений.
Примеры.
По Гейне. Число В наз. Приделом функции при Х->а если какую бы последовательность
Xn->a мы не взяли последовательность Функции сходится к В.
По Коши. Число В называется пределом Функции при х-> а если (для всех Епсл>0)
Найдется такое b>0(Епсл.),что для всех Х,
Удовлетворяющих неравенству 0<|x-a|<b
Выполняется |F(x)-B|<Епсл.
Они эквивалентны.
Утверж.
Для того, чтобы существовал предел Необходимо и достаточно чтобы левый Предел равнялся правому.
15. Односторонние пределы функции и их связь с обычным двухсторонним пределом.
Примеры.
Односторонний предел-предел числовой Функции, подразумевающий,приближение, к
Предельной точке с одной стороны(левосторонний И правосторонний).
Опр.2
Для существования (двустороннего) предела Функции необходимо и достаточно, что бы оба Односторонних предела существовали и Равнялись друг другу.
16. Обобщения понятия предела функции.
Примеры.
Понятие предела можно обобщить Для случая когда аргумент функции Или ее значения стремятся к бескон.
Например: LimF(x)= беск.,если для Любого (епсл>0)(существует b>0),что Для всех Х, таких что X0<X<X0+b
Выполняется |F(x)0|>Епсл.
17. Бесконечно малые и бесконечно большие функции. Роль бесконечно малых функций в теории пределов. Примеры.
Функция F(x) называется Б.М. при x->a
Если ее предел равен 0 |Lim F(x)|=0
Теорема. Для того чтобы число было Предельной функцией при х->а
Необходимо и достаточно что бы

Функция имела вид:
F(x)=b+a(x)где F(x) б.м.
18. Свойства пределов функций
(3-4 из них с доказательством). Примеры.
1.Lim c*F(x)=c*Lim F(x)
2.Lim(F(x)+-g(x))=LimF(x)+-Lim g(x)
3.LimF(x)*g(x)= LimF(x)*Lim g(x)
4.Lim F(x)/g(x)= Lim F(x)/Lim g(x), если
Lim g(x)!=0
19. Первый замечательный предел и следствия из него. Примеры.
Lim sinx/x=1
Lim tgx/x= limsinx/(cosx-x)=lim 1/cosx=1
20. Второй замечательный предел.
Примеры.
(1^беск) lim(1+1/x)^x=e (1^беск) Lim(cosx)^1/x^2 e^lim cosx-1/x^2=e^(-1/2)
(0/0)lim ln(1+x)/x=lim ln(1+x)^1/x=lne=1
21.Сложная функция придел сложной функции.
Сложная функцияфункция от функции. Если
Z- функция от Y,т.е. Z(Y) ,а Y функция от Х,
Т.е. Y(X),то Z(Y(X))-назыв.сложной функц.
22. Критерий Коши существования предела функции.
Критерий Коши существования предела функции N переменных (n 1). Для того, чтобы существовал предел lim f(x), xa, необходимо и достаточно,
чтобы для любого >0 окрестность U=U(a), точки такой, что для всех x’ U и x’’ U выполнялось неравенство p(f(x), f(x’)) <
23. Пределы монотонных функций.
Функция f : E → R называется строго возрастающей на E,
если для всех x1, x2 E таких, что x1 < x2 = f(x1) < f(x2);
возрастающей на E, если для всех x1, x2 E таких, что x1 < x2 = f(x1) 6 f(x2); убывающей на E, если для всех x1, x2 E таких, что x1 < x2 = f(x1) > f(x2); строго убывающей на E, если для всех x1, x2 E таких, что x1 < x2 = f(x1) > f(x2).
Функции перечисленных типов называются монотонными на множестве E
Теорема о пределах монотонных функций:
Для того чтобы возрастающая на множестве E функция f : E → R имела левый предел при x → b − 0, x E, необходимо и достаточно, чтобы она была ограничена сверху, а для того чтобы она имела правый предел при x → a + 0, x E, необходимо и достаточно, чтобы она была ограничена снизу.
Необходимость. Если этот предел существует, то, как и всякая функция, имеющая предел (теорема 1.10.1 §

1.10), функция f оказывается финально-ограниченной при x → b − 0, а следовательно, и ограниченной сверху на E (ведь функция f — возрастающая на E).
Достаточность. Если f ограничена сверху, то существует sup f(x) = A; при x E
24.(a) Сравнение Б.М. функций
LimF1(x)=0; lim F2(x)=0
Чтобы их сравнить кто меньше нужно найти
Lim F2(x)/F1(x)
Если предел=0, это значит что F2(x) <F1(x)
Если предел=1, F2(x)эквивалентен F1(x)
Если предел=A(!=1,!=0)то F1(x) и F2(x)
Одного порядка
24.(b)Сравнение Б.Б. функций
Lim|F1(x)|=беск.: lim|(F2(x)|=беск.
Тот же принцип
Lim F2(x)/F1(x) Если lim=0,тоF2(x)
Называется беск.большой функцией низшего Порядка роста.
Если lim=1,то F2(x)эквивал.F1(x)
Если lim=А,то F2(x) и F1(x) одного порядка роста.
25. Прим. Эквивалентных Б.М.,при вычислении пределов
Lim(x->3) sin(x-3)/s^2-4x+3=lim(x-3)/(x-3)(x-1)= =Lim1/(x-1)=1/2
26. Различные определения непрерывности функции в точке. Примеры.
1)Основное определение. Функция y=f(x) называется
непрерывной в точке x0 pf, если предел функции при xx0 равен значению функции в той точке lim (x) x0 ; f(x)=f(x0)
2)На языке Функция y=f(x) называется
непрерывной в точке x0 , если |
, |
>0 , такое, что |
|||
x |
( |
) |
( |
) |
( ) |
3)На языке последовательности по Гейне Функции y=f(x) называется непрерывной в точке x0, если для любой последовательности, сходится в точке x0, соответствующая последовательность значений
функции сходится к f(x0) xn x0 => f(xn) f(x0)
4) На языке приращений Функция f(x) называется непрерывной в точке x0, если бесконечно малому

приращению аргумента соответствует бесконечно малому приращению функции
27. Точки разрыва функции и их классификация. Примеры.
Определение 3.2 Точка  называется точкой разрыва функции
называется точкой разрыва функции  , если она определена в
, если она определена в
некоторой проколотой окрестности точки  (то есть определена на некотором интервале, для
(то есть определена на некотором интервале, для
которого  служит внутренней точкой, но в самой
служит внутренней точкой, но в самой
точке  , возможно, не определена) и выполняется хотя бы одно из следующих условий:
, возможно, не определена) и выполняется хотя бы одно из следующих условий:
1)не существует предела слева  ;
;
2)не существует предела справа  ;
;
3)пределы слева  и
и
справа  существуют, но не равны друг другу:
существуют, но не равны друг другу:  ;
;
4) пределы слева 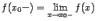 и справа
и справа  существуют и равны друг
существуют и равны друг
другу:  , но не совпадают со значением функции в точке
, но не совпадают со значением функции в точке  :
:  , или функция
, или функция  не определена в точке
не определена в точке  .
.
Если имеет место либо случай 3, либо случай 4, то точка
разрыва  называется точкой разрыва первого рода,
называется точкой разрыва первого рода,
а поведение функции в окрестности точки  называется разрывом первого рода в
называется разрывом первого рода в
точке  ;
;
в случае 4 точка разрыва первого рода называется устранимой точкой разрыва, а разрыв
функции в этой точке  устранимым разрывом.
устранимым разрывом.
Если же имеет место либо случай 1, либо случай 2 (либо и тот и другой сразу), то точка разрыва
 называется точкой разрыва второго рода, а
называется точкой разрыва второго рода, а
поведение функции в окрестности этой точки
 разрывом второго рода в точке
разрывом второго рода в точке  .
.
28. Свойства функций, непрерывных в точке. Замечательные следствия второго замечательного предела.
1) Говорят, что функция f: E R, непрерывна в точке
x0 E (x0 – предельная точка множества E), если
2) Говорят, что функция f : E → R непрерывна в точке x0E, если
ε > 0 δ > 0 x E(|x − x0 | < δ = |f (x) − f (x0 )| < ε) .
3) Говорят, что функция f : E → R непрерывна справа в точке x0 E , если
ε > 0 δ > 0 x E(0 x − x0 < δ = |f (x) − f (x0 )| < ε)

4) Функция f : E → R называется непрерывной на множестве E, если она непрерывна в каждой точке множества E. Множество всех непрерывных функций, определенных на E, обозначают C(E).
29. Функции, непрерывные на множестве. Теорема Вейерштрасса.
Пусть  и
и 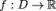 .
.
Функция  непрерывна в точке
непрерывна в точке  , если для
, если для
любого  существует
существует  такое, что для любого
такое, что для любого
Функция  непрерывна на множестве
непрерывна на множестве  , если она
, если она
непрерывна в каждой точке данного множества.
В этом случае говорят, что функция  класса
класса  и пишут:
и пишут:  или, подробнее,
или, подробнее,  .
.
1 теорема Вейерштрасса.
Если f непрерывна на [a, b], то она ограничена на нем, т.е. существует такое число M , что |f (x)| M , при всех x [a, b].
2 теорема Вейерштрасса.
Если f непрерывна на [a, b], то она достигает на нем своей верхней и нижней грани.
30. Функции, непрерывные на множестве. Теорема о промежуточном значении непрерывной функции.
Теорема:
Функция называется непрерывной на множестве, если она непрерывна в каждой точке множества. То, что f(x) непрерывна на множестве X обозначается следующим образом: f(x)ОCX.
Следствие 1. f непрерывна на [a,b], f(a)¹f(b). Тогда для "M из промежутка f(a), f(b) $cÎ[a,b]:f(c)=M.
Следствие 2. Пусть f(x) непрерывна на [a,b], m=inf f(x), M = sup f(x), тогда множеством значений этой функции будет отрезок [m,M].
31.Обратная функция. Непрерывность обратной функции
Обратная функция-функция оброщающая заывисимостть,
Выражаемую данной функцией F^(-1) (x)
Теорема. Если функция F:X-> Y, где н=F(X),обратина,то для
Нее существует единственная обратная функция F^(-1):Y->X
И если y=F(x), то x=F^(-1) (y), и если x=F^(-1) (y),то
F^(-1) (F(x))=X при любом y прин. Y
32.Понятие производной функции. Физ. Смысл производной.
Касательная.
y=kx*b –прямая
y=F’(X0)*x+b
F(X0)=F’(X0)*X0+b
b=F(X0)-F’(X0)*X0
y=F’(X0)*X+F(X0)-F’(X0)*X0

y=F(X0)+F’(X0)(X-X0) – уравнение касательной
к графику y=F(x) в точке с абсциссой Х0.
Опр. Пусть функция определена в точке и в ее окрестности,
Тогда мы можем говорить приращение функции Y=F(X0- X)-F(X0)
y=X^2; X0=1
y=(X0- x)^2-X0^2=1+2 X+ X^2-1=2 X+ X^2 y/( X) – разностное отн-е
Опр.1 Конечный предел разностного отношения при X- >0
Наз. Производной функции в т. X0
Lim( X->0) F(X0+ X)-F(X0)/ X=F’(X0)
Опр.2 Функция называется диф-мой в т. X0,если приращение может
Быть представлена в виде y=A* X+O( X)
Теорема. Для того чтобы функция была диф. Необходимо и достаточно
Чтобы у нее сущ. Производная в этой точке
Y=e^x; lim( X->0) (e^X+ X)/ X=lim e^X (e^ X)-1/KX=e^x (e^x)’=e^x
33, 34, 35. Геометрический и физический смысл производной. Дифференциал.
Опр. Пусть функция диф-ма в т ky=y’(x0)kx+o(kx) при kx->0
ky=y’(x0)kx главная линейная относительно kx часть приращения
функции, отличая от этого приращения на Б.М. наз. Дифференциалом.
dy=y’(x)dx ky=dx DC=AC tga
DC=kx*y’(x0)
Дифференциал геометрически – есть приращение ординаты касательной.
Ф. y(x0+kx) приближенно = y(x0)+y’(x0)-kx
Пример. Sqrt(4.12) y= sqrt(x) x0=4 4.12=4+kx
