mo_in_exercises

Отсюда и из квадратичного вида функции Q(x) следует существование

конечного минимума в задаче, поскольку на бесконечности функция будет возрастать равномерно по параметру c .

Исследуем границу x3 − x1 =1. Система условий Куна-Таккера примет

вид:

− x3 = −λ1, x3 − x1 =1

− x1 = λ1, λ ≥ 0,

где λ1– множитель Лагранжа. Они выполняются при x1 = −0.5, x3 = 0.5, λ1 = 0.5. Значение функции равно −0.25 (точка A на рис. 3.4).

Исследуем границу x1 − x3 = 2 . Для нее имеем следующую систему необходимых условий локального минимума:

− x3 = λ1, x1 − x3 = 2

− x1 = −λ1, λ ≥ 0.

Они выполняются при x1 = +1, x3 = −1, λ1 =1 (точка B на рис. 3.4).

Значение функции равно −1, т.е. меньше, чем в первой найденной точке. Следовательно, глобальный минимум вспомогательной задачи достигается в

точке x1 =1, x3 = −1, а для исходной задачи — в точке x1 =1, x2 = 3,

x3 = −1.

Рис. 3.4. Структура задачи на линейном многообразии, порожденном ограничениемравенством (стрелками показаны направления возрастания функции)

Дополнительный материал и задачи по данному разделу можно найти в литературе [5, 8-16].

41

постройте внешние нормали к границам, а также вектор − Q(x) . Используя

геометрическую трактовку условий Куна-Таккера, ответьте на вопрос: может ли точка глобального минимума располагаться в одной из вершин? На основе полученных результатов сделайте выводы о возможном положении точки условного минимума. Проверьте Ваши предположения с помощью теоремы Куна-Таккера, найдите решение.

3. Используя геометрические представления, укажите точку минимума в

задаче min{x2 : x12 + x22 ≤1; − x1 + x22 ≤ 0; x1 + x2 ≥ 0}.

Обоснуйте полученные результаты с помощью условий Куна-Таккера.

4. Проверьте выполнение условий Куна-Таккера в точках (0;2), (0;0),

( 2;0), (1;0), (0.05;0) для задачи: min {10x12 +5x22 − x1 + 2x2 −10 : x D},

условиям неотрицательности множителей Лагранжа.

Указание: Решите задачу, рассмотрев четыре возможных случая относительно множества I ( y) , содержащего номера неравенств, на границе которых находится проекция точки y : I ( y) = ,{1},{2},{1, 2}.

42

Указание: если предположить, что активно одно ограничение x2 ≤ x13 , то

может возникнуть проблема с аналитическим определением значения множителя Лагранжа. Попробуйте оценить его знак без явного вычисления.

10. На классе гладких задач исследовать область D на регулярность,

Ваши выводы, если из описания области D исключить последнее неравенство

x1 ≤ 0 ?

11. Найдите решения следующих задач:

43

15. На допустимом множестве, заданном следующими ограничениями:

3 + x1 − x3 ≥ 0, 0 ≤ x1 ≤ 2, 15 + x1 ≤ 5x3 , 2x1 + x2 = 2. Решите задачу

определения минимума функции 24x12 + x22 + 4x32 −8x1x3 −12x3 +36x1 − x2 .

16. Найдите глобальный минимум в задаче

18. С использованием теоремы Куна-Таккера докажите, что из всех треугольников с общим углом при вершине и заданной суммой длин боковых сторон равнобедренный треугольник имеет наименьшее основание.

19. В углах прямоугольной заготовки с размерами A на B вырезают квадраты с размерами x на x . Из оставшейся части собирают коробку. Определите значение x , при котором объем коробки максимален.

20. Найдите разложение положительного числа R на N вещественных сомножителей так, чтобы их сумма была минимальной.

21. Рассмотрите задачу о ритмичности производства (задачу № 11 из раздела 1), предполагая, что сырье не является штучным, т.е. значения xi не целочисленны. Решите задачу при следующих значениях параметров: N = 5,

E0 = 5, E = 5, A = 20 , P1 = 6 , P2 = 5 , P3 = 3, P4 =1, P5 = 4 ; а также при

N = 5, E0 =1, E = 3, A =15, P1 =1, P2 =1, P3 = 5 , P4 = 5 , P5 = 4 .

22. Найдите глобальные минимумы в задаче:

единственность.

44

4. Вычислительные методы математического программирования

4.1. Основные понятия

Вычислительным методам решения задач математического программирования посвящена обширная литература [8-11, 13, 17, 18, 19].

Вобщем случае задача математического программирования представима

ввиде:

где E - множество простой геометрической структуры, например, E = Rn или E = {x : ai ≤ xi ≤ bi , i =1,K, n}. Постановка (4.1)-(4.2) зависит от набора

функций, представимого вектор-функцией f = (Q, g1,K, gN , h1,K, hM ). Вычислительный метод должен строить для задачи (4.1)-(4.2) оценку

решения ek (интервальную или точечную) по координатам или по значению

образуют множество поисковой информации ωk ={(xs , Js ) : s =1,K, k}.

Вычислительный метод α (или алгоритм) решения задачи (4.1)-(4.2)

строится исходя из имеющейся априорной информации о свойствах функций f и представляет набор правил α = Pk (ωk ), Ek (ωk ), M k (ωk ) , k = 0,1,K

( μk = 0 - нет останова, μk =1 - останов).

Одним из принципов построения методов оптимизации является принцип наилучшего гарантированного результата. Он может быть использован, если

для класса решаемых задач Φ ={f } и выбранного класса алгоритмов A ={α} можно ввести функцию эффективности d(α, f ) , показывающую, насколько удачным было применение α к задаче f . Например, значение d можно

46

трактовать как меру остаточной погрешности в оценке решения задачи f с использованием метода α .

Функцию d* (α) называют гарантированной эффективностью метода

α на классе Φ, если d * (α) = sup{d (α, f ) : f Φ}.

Заметим, что оптимального метода может не существовать, но ε -оптимальный всегда существует.

Кроме введенного понятия оптимальности по отношению к априорной информации о функции ( f Φ), при построении методов широко использует-

ся понятие последовательной оптимальности, в частности, одношаговой оптимальности, учитывающее текущую поисковую информацию.

Пусть метод α уже выполнил k испытаний, результаты которых запомнены в виде поисковой информации ωk . Обозначим через Φωk

апостериорный класс функций

Φωk = { f Φ : (xs , Js ) ωk : J (xs , f ) = Js }.

Таким образом, в классе Φωk содержатся те функции из исходного класса Φ,

результаты испытаний которых во всех точках xs уже проведенных испытаний совпадают с имеющимися результатами Js этих испытаний. Функции из Φωk

неразличимы по результатам испытаний в точках xs ( s =1,K, k ).

Пусть функция d(ωk ) описывает эффективность проведенных

испытаний. Гарантированной эффективностью очередного испытания в точке x называют

d*(ωk , x) =sup{d(ωk (x, J)): J = J(x, f ), f Φωk }.

Говорят, что метод α последовательно оптимален на один шаг вперед

(одношагово оптимален), если выбор следующего испытания подчиняется условию

xk +1 = arg inf { d* (ωk , x) : x E},

Если нижняя грань в определении xk +1 не достигается, используют значение x , обеспечивающее ее ε -приближение.

47

4.2. Поиск минимума унимодальной функции на отрезке

Пусть Φu - класс функций Q, унимодальных на отрезке

должны иметь на этом отрезке единственный глобальный минимум (обозначим его x*) и строго убывать на [a, x*], а на [x*,b] – строго возрастать. Унимодаль-

ные функции не обязаны быть непрерывными. Их испытания включают только измерения значений функции.

« argmin» понимается номер испытания с наименьшим значением. Тогда

x* [xk* (Q)−1, xk* (Q)+1].

Заметим, что здесь под x0 и xN +1, по определению, понимаются точки a и b, в которых измерения не проводятся. Данный интервал является оценкой

случае не только номер k*(Q) , но и координаты самих точек измерений xk зависят от функции Q .

N -шаговые пассивные методы

Если метод αN проводит ровно N измерений, то такой метод называют N -шаговым. Если для метода αN правила Pk выбора точек испытаний не зависят от накопленной поисковой информации ωk , то метод называют пассивным. Пассивный N -шаговый метод αNпас полностью определяется набором точек измерений a < x1 < x2 <K< xN < b , положение которых не

зависит от минимизируемой функции. Для таких методов функцию эффективности можно принять в виде

d (αNпас, Q) = xk * (Q)+1 − xk * (Q)−1;

гарантированная эффективность на классе Q Φu примет вид

d * (αNпас) = max{xk +1 − xk −1 : k =1,K, N}.

Это позволяет построить для каждого N оптимальные или ε - оптимальные пассивные алгоритмы, гарантированная эффективность которых

48

исходного интервала невысока за счет пассивного характера поиска. Последовательные методы могут обладать лучшей эффективностью.

Метод дихотомии – неоптимальный последовательный метод

Это простой последовательный метод, позволяющий сокращать интервал поиска в два раза с использованием каждых двух новых измерений. Первое измерение не приводит к сокращению интервала. Данный метод не является ни оптимальным, ни ε -оптимальным.

Описание алгоритма

(a)Задать δ > 0 – точность решения.

(b)Положить c = (a +b)2 и Qc =Q(c) .

(c)Пока b −a >δ , выполнять пункт (d), иначе – перейти на пункт (e).

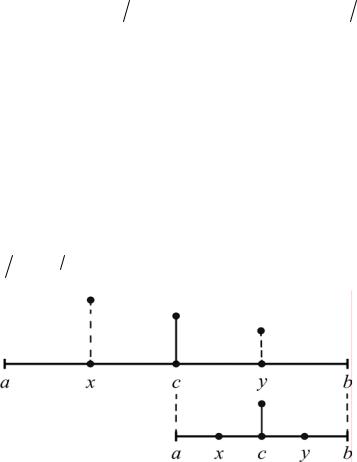
Рис. 4.1. Один из трех возможных случаев сжатия интервала поиска в методе дихотомии после двух новых измерений в точках x и y

Метод золотого сечения и метод Фибоначчи

Рассмотрим методы, которые для очередного сжатия интервала поиска используют только одно новое измерение (кроме начального этапа, требующего проведения сразу двух измерений). Исходя из симметрии задачи, первые два

измерения в точках x2 и y2 целесообразно размещать симметрично

49

относительно центра интервала, а на вновь образованных интервалах новое измерение проводить в точке, симметричной точке прежнего измерения, существующей внутри интервала (рис. 4.2).

Обозначим через λk доли, составленные длинами соответствующих

частей текущего интервала по отношению к его собственной длине. Из рис. 4.2 вытекает следующая их взаимосвязь:

Метод золотого сечения использует постоянную пропорцию деления λk =τ = ( 5 −1) 2 , полученную как стационарное решение уравнения (4.3).

Описание алгоритма

(a) Задать δ > 0 - точность решения.

(b) Провести измерение в точке y = a + (b − a) τ , Qy = Q( y) и построить новую точку x = b − (b − a) τ .

(c)Пока b −a >δ , выполнять пункт (d), иначе – перейти на пункт (e).

(d)Провести измерение в новой точке ( x или y ) и запомнить результат

(в Qx или Qy ). Если Qx < Qy , то положить b := y , y := x , Qy := Qx и выбрать новую точку x =b −(b −a) τ ; иначе, при Qx > Qy , положить a := x , x := y , Qx := Qy и выбрать новую точку y = a + (b − a) τ . Вернуться к пункту (c).

(e) полученный интервал [a,b] принять в качестве интервальной оценки

решения.

Гарантированная эффективность метода золотого сечения за N измерений d * (αNз.с. ) = (b − a) τ N −1 < d * (αNдих. ) .

Метод Фибоначчи построен американцем Дж. Кифером (J. Kiefer) в 1953 году и назван в честь использованной в нем последовательности чисел

50