3. Классические эффекты в динамике линейных осцилляторов

3.1.Динамика линейного осциллятора

3.1.1.Модель

Математическая модель линейного осциллятора представляет собой линейное дифференциальное уравнение второго порядка:

Это уравнение описывает широкий класс процессов в системах различной природы (механических, электрических, экономических и т.д.). При этом параметры модели имеют соответствующий смысл. Например, для физического маятника (грузик на пружине с закрепленным концом, движущийся с вязким трением) за основу берется второй закон Ньютона (равенство для сил):

получаем уравнение (3.1), где 2δ = h / m и ω2 = k / m . Для электрического колебательного контура (катушка, резистор и конденсатор) имеет место закон Кирхгофа (равенство для падений напряжения): Lq&&= −Rq& −q / C (q – заряд конденсатора, L – индук-

тивность катушки, R – сопротивление резистора, C – емкость конденсатора) или Lq&&+ Rq& +q / C = 0 , откуда после деления на

L получаем уравнение (3.1), где 2δ = R / L и ω2 =1/ (CL) .

Уравнение (3.1) задает динамическую систему, состоянием которой является (x, x&) . В этой системе имеется состояние рав-

новесия x = x& = 0 , которое в зависимости от корней характеристического уравнения λ2 +2δλ +ω2 = 0 может иметь различный тип. В свою очередь, характеристические корни λ1,2 зависят от параметров δ и ω2 .

73

Если на осциллятор действует внешнее гармоническое возмущение F0eiνt (в механическом случае – сила, в электрическом

– ЭДС), то система описывается линейным неоднородным дифференциальным уравнением:

При δ > 0 (положительное трение) собственные колебания осциллятора затухают, и устанавливаются вынужденные колеба-

ния, которые можно записать в виде x(t) = F0 K(iν)eiνt или

x(t) = F0 A(ν)ei[νt +ϕ( ν)] . Величина K(iν) = A(ν)eiϕ( ν) (комплексный коэффициент усиления амплитуды внешнего воздействия) назы-

вается амплитудно-фазовой частотной характеристикой

(АФЧХ) и графически изображается в виде годографа на комплексной плоскости ( ν изменяется от 0 до +∞ ). Величина A(ν)

(отношение амплитуды вынужденных колебаний к амплитуде внешнего воздействия) называется амплитудно-частотной характеристикой (АЧХ), а величина ϕ(ν) (фазовый сдвиг вынуж-

денных колебаний по отношению к вынуждающим) – фазово-

частотной характеристикой (ФЧХ).

При определенном значении внешней частоты ν = ν* , зависящем от параметров осциллятора, значение АЧХ достигает максимума, т.е. вынужденные колебания происходят с наибольшей амплитудой. Это явление называется резонансом, а само значе-

ние ν = ν* – резонансной частотой.

3.1.2. Реализация в AnyLogic

Работа реализована в файле Part2\Oscillator.alp (рис. 3.1). В окне анимации с помощью радиокнопки из группы радиокнопок «Колебания» можно выбирать тип исследуемых колебаний (собственные или вынужденные).

В режиме «Собственные колебания» в левой части окна рисуется бифуркационная диаграмма на плоскости параметров

(ω 2 ,δ) , на которой с помощью точки (маленького прямоуголь-

74

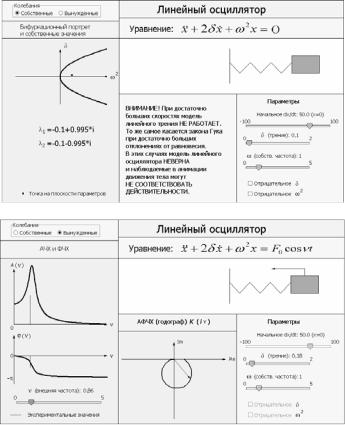
Рис. 3.1

ника) выводятся текущие значения параметров, под диаграммой – значения собственных чисел (характеристических корней) λ1,2 . В

правой части окна – анимация колеблющегося грузика на пружи-

не с возможностью изменения параметров δ , ω2 и начальной скорости dx / dt (начальное значение x при изменении dx / dt автоматически делается равным нулю). С помощью флажков можно

изменять знак параметров δ и ω 2 .

75

В режиме «Вынужденные колебания» выводятся графики АЧХ и ФЧХ, а также годограф АФЧХ (при этом значение АФЧХ изображено в виде радиус-вектора). При этом, кроме теоретических графиков АЧХ и ФЧХ, выводятся экспериментальные значения этих характеристик, вычисляемые в каждый момент времени по формуле:

В правой части окна имеется анимация колеблющегося грузика на пружине, на который действует внешняя гармоническая сила, показанная стрелкой (длина стрелки указывает модуль силы, а направление стрелки соответствует направлению силы). С помо-

щью бегунков можно менять параметры осциллятора δ и ω 2 , начальное значение скорости dx / dt (начальное значение x при изменении dx / dt автоматически делается равным нулю), а также (под графиками АЧХ и ФЧХ) частоту внешнего воздействия ν .

Флажки изменения знаков параметров δ и ω 2 в этом режиме недоступны (так как АФЧХ не имеет смысла при отрицательном

δ или ω2 из-за неустойчивости собственных колебаний).

3.1.3. Задания для эксперимента

1.Запустите модель в AnyLogic.

2.Пронаблюдайте за эволюцией типов собственных движений грузика в анимации, а также фазового портрета и осциллограмм фазовых переменных при изменении параметров осциллятора. Согласуется ли видимое вами на экране с теорией?

76