Физика гетероструктур

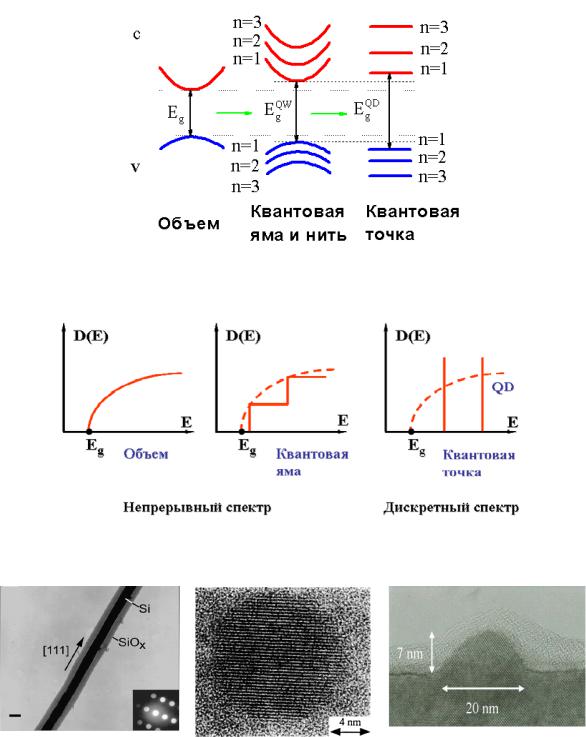
Зонные спектры расщепляются на подзоны размерного квантования для квантовых ям и нитей и на дискретные уровни для квантовых точек (Рис. 2.4). В результате, в плотности состояний низкоразмерных систем возникают характерные особенности (рис. 2.5).

Рис. 2.4. Трансформация энергетического спектра элементарных наноструктур.

Рис. 2.5. Плотность состояний элементарных наноструктур.

На рисунке 2.6 представлены изображения реальных элементарных наноструктур, полученные с помощью электронного микроскопа.

Рис. 2.6. Изображения (слева направо) квантовой нити, квантовой точки CdS в SiO2, квантовой точки InAs в GaAs, полученные с помощью просвечивающего электронного микроскопа.

Из элементарных наноструктур можно построить сложные наноструктуры, например, многослойные квантовые ямы и сверхрешетки (рис. 2.7),

17

одномерные и двумерные массивы квантовых нитей или двумерные и трехмерные массивы квантовых точек (рис. 2.8).

Рис. 2.7. Изображение многослойной структуры из квантовых ям, полученное с помощью просвечивающего электронного микроскопа.

Рис. 2.8. Изображения (слева направо) двумерного и трехмерного массива квантовых точек, полученные с помощью просвечивающего электронного микроскопа.

Наличие размерных зависимостей параметров наноструктур неоднократно подтверждалось экспериментально и, прежде всего, оптическими методами. Еще в 1962 году Сандомирский предсказал, что край фундаментального поглощения света в тонких пленках кристаллов должен смещаться в синюю область спектра при уменьшении их толщины Lz в соответствии с формулой

Eg = 2mL2z .

Вопрос о первом экспериментальном наблюдении эффекта размерного квантования остается открытым. Вероятно, что такие наблюдения были сделаны довольно давно, но целенаправленное изучение этого эффекта начинается именно в 60 годы.

18

§ 2.2. Размерное квантование электронной подсистемы квантовых точек

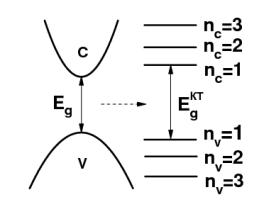
Эффект размерного квантования заключается в том, что при уменьшении линейных размеров объекта квазинепрерывные энергетические спектры и волновые функции его элементарных возбуждений радикально модифицируются. В случае квантовых точек вместо непрерывного спектра возникают дискретные уровни размерного квантования (рис. 2.9). Рассмотрим этот эффект для случая полупроводниковых квантовых точек простой формы, встроенных в диэлектрическую среду.

Рис. 2.9. Схема, иллюстрирующая трансформацию непрерывного энергетического спектра зоны проводимости Ec(k) и валентной зоны Ev(k) объемного полупроводника в дискретный спектр состояний квантовой точки. Eg и EgКТ – ширины запрещенной зоны в объемном материале и в

квантовой точке.

Для описания энергетического спектра и волновых функций низкоразмерных систем наиболее часто используется та или иная форма метода эффективной массы (kP-теория возмущений), детально разработанного для объемных твердых тел. Привлекательность этого подхода основана на том, что он в ряде случаев позволяет получать аналитические результаты, явно учитывающие граничные условия и форму наноразмерных структурных элементов. Кроме того, в рамках kP-теории возмущений относительно легко учесть взаимодействия электронной подсистемы низкоразмерных систем с колебаниями решетки, статическими деформациями и внешними полями. Удивительным успехом данного подхода является то обстоятельство, что он позволяет объяснить многие качественные закономерности, присущие низкоразмерным системам, даже на основе простейшей двухзонной модели полупроводника, которая явно учитывает лишь одну зону проводимости (c) и одну валентную зону (v).

Основная идея kP-теории возмущений заключается в том, что волновая функция электрона (дырки) представляет собой линейную комбинацию произведений быстро осциллирующих в области элемен-

19

тарной ячейки кристалла блоховских амплитуд un(r) и медленно меняющихся в масштабе элементарной ячейки огибающих волновых функций ϕn(r)

Φ(r)= ∑ϕn (r)un (r) . (2.1)

n

В (2.1) суммирование ведется по вырожденным состояниям. В случае простой орбитально-невырожденной зоны (например, зоны проводимости в прямозонных полупроводниках A3B5) в (2.1) остается лишь одно слагаемое, используя которое, можно получить с помощью стандартной процедуры уравнение Шредингера для огибающих волновых функций квантовой точки

где m* – эффективная масса носителя заряда в рассматриваемой зоне, а V(r) – трехмерная потенциальная яма, которая пространственно ограничивает движение носителей заряда. Отсюда следует, что для однозонной модели квантовой точки задача на собственные значения сводится к хорошо известной из курса квантовой механики задаче о движении частицы в потенциальной яме.

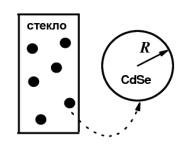
Рис. 2.10. Квантовые точки в стеклянной матрице, представляющие собой сферы с радиусом R.

Известно, что в ряде случаев уравнение (2.2) может быть решено аналитически. Прежде всего, предположим, что потенциальная яма V(r) обладает бесконечно высокими стенками. Это предположение является вполне оправданным, если квантовая точка находится, например, в стеклянной матрице. Будем считать также, что квантовая точка представляет собой сферу радиуса R (рис. 2.10). Тогда потенциальная яма имеет вид

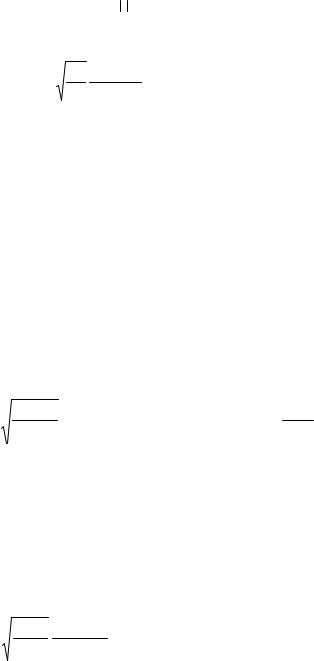
Благодаря сферической симметрии задачи переменные в (2.2) разделяются. Волновые функции и энергии электрона (дырки) в квантовой точке при условиях ϕ(0)≠ ∞ и ϕ(r)|r =R = 0 определяются следующими выра-

жениями:

В (2.4) n, l и m – главное квантовое число, угловой момент и его проекция, соответственно, jl(x) и Ylm(Ω) – сферические функции Бесселя и сферические гармоники, knl=ξnl/R, ξnl – n-й корень функции Бесселя l-го порядка (jl(ξnl)=0). Из (4.4.) прямо следует, что трехмерное пространственное ограничение движения носителей заряда в квантовой точке приводит к расщеплению их непрерывного энергетического спектра Ec(v) (k) = h2k2 / 2mc(v) на дискретные уровни размерного квантования Enl

(рис. 2.9). Кроме того, оказывается, что энергия дискретных уровней обратно пропорциональна квадрату радиуса квантовой точки. Аналогичные результаты могут быть получены для квантовых точек в форме прямоугольного параллелепипеда:

где вектором n=(nx,ny,nz) обозначен набор трех квантовых чисел nx, ny и

случае цилиндра с высотой h и радиусом основания ρ0 волновые функции и энергии равны

knl=ζnl/ρ0, ζnl – n-й корень функции Бесселя l-го порядка (Jl(ζnl)=0).

До сих пор мы рассматривали одночастичные состояния электронной подсистемы квантовых точек (2.4)-(2.6), однако во многих случаях интерес представляют ее двухчастичные состояния. Это связано с тем, что при межзонных переходах в квантовых точках, как и в объемных полупроводниках, возникают электрон-дырочные пары. Разноименно

21

заряженные частицы, составляющие пару, связаны друг с другом кулоновским взаимодействием, которое меняет ее энергию и может приводить к образованию экситона. Чтобы выяснить пределы применимости одночастичного описания электронной подсистемы квантовой точки, сравним суммарную энергию размерного квантования электрона и дырки Esum=Ecn+Evn с энергией их кулоновского взаимодействия |Vcoul|=e2/(ε0|rc-rv|). Здесь ε0 – низкочастотная диэлектрическая проницаемость материала квантовой точки, а rc и rv – координаты электрона и дырки. Очевидно, что кулоновскими поправками к энергии электрондырочной пары можно пренебречь при выполнении неравенства Esum >>|Vcoul|. Для сферической квантовой точки с радиусом R при условии, что |rc-rv|≈R, это неравенство сводится к

Rex = εμ0h2 >> R , (2.7) e2

где μ=mc mv/(mc+mv) – приведенная масса электрона и дырки. Таким образом, одночастичное описание электронного энергетического спектра квантовой точки применимо, если боровский радиус экситона Rex существенно превышает ее радиус R. Про такие квантовые точки говорят, что они находятся в режиме сильного конфайнмента (пространственного ограничения). Противоположный предельный случай Rex <<R принято называть режимом слабого конфайнмента, или экситонным режимом.

Рассмотрим квантовую точку с электроном в зоне проводимости и дыркой в валентной зоне, которые связаны кулоновским взаимодействием. В отличие от (2.2) такая система описывается следующим уравнением Шредингера:

где два первых слагаемых в левой части уравнения соответствуют кинетическим энергиям электрона и дырки, V (rc ,rv )=V (rc )+V (rv ) – сумма

трехмерных потенциалов для частиц, образующих электрон-дырочную пару. Отметим, что уравнение Шредингера (2.8) не может быть решено точно даже в простейшем случае сферической потенциальной ямы V (rc(v) )с бесконечно высокими стенками (2.3). Это связано с тем, что мы,

по существу, имеем дело с задачей трех тел, в которой роль третьей частицы играет потенциальная яма. Получим приближенное аналитическое решение уравнения (2.8), которое наиболее близко по форме к решению хорошо известной задачи об экситоне Ванье – Мотта в объемном полупроводнике. Для этого в (2.8) перейдем к системе координат, связанной

22

с движением центра масс электрона и дырки и их относительным движением,

X = (mcrc + mvrv )/ M , x = rc −rv , (2.9)

где M=mc+mv. В этих координатах уравнение (2.8) имеет вид

причем потенциал квантовой ямы приобретает достаточно сложную форму V (x, X)=V (X + ρvx)+V (X − ρcx), где ρc(v)=mc(v)/M, и не допускает разделения переменных. Таким образом, собственные функции задачи об экситоне в квантовой точке ϕ(x,X), вообще говоря, нельзя представить в виде произведения волновых функций, описывающих движение его центра масс ϕ(X) и относительного движения электрона и дырки ϕ(x). Чтобы обойти эту трудность в режиме слабого конфайнмента (Rex <<R) вместо V (x, X) используют «псевдопотенциал», который выбирают из условий физической разумности и максимальной простоты. Вместо часто применяется потенциал V (X), имеющий форму (2.3). Такая аппроксимация уместна, поскольку для положения центра масс естественным, хотя и несколько завышенным, граничным условием является неравенство |X| ≤ R. Очевидно, что указанная замена – достаточно грубое приближение – приводит к существенным потерям при описании экситона в квантовой точке. Действительно, потенциал учитывает влияние конфайнмента только на трансляционное движение экситона как целого, относительное же движение электрона и дырки остается невозмущенным. Единственным, но очень важным достоинством V (X) является чрезвычайная простота такого потенциала, позволяющая точно решить задачу о движении экситона. В результате для сферической квантовой точки собственные функции и собственные энергии экситона определяются выражениями

где ϕn'l 'm' (x) – водородоподобные волновые функции объемного экситона

23

в состояниях относительного движения, характеризуемых квантовыми числами n’, l’ и m’, Nn'l'=2 [(n’-l’-1)!/((n’+l’)!)3]1/2/n’2,

F (x) = xl 'e−x / 2L2l−'+1− (x) ,

n'l ' n' l ' 1

Lab (x) – обобщенный полином Лагерра; волновая функция ϕnlm (X), описывающая трансляционное движение экситона, совпадает с выражением (2.4), в котором нужно сделать замену r→X; Eg – ширина запрещенной зоны объемного полупроводника; En’=Ry/n’2 – энергии ионизации уровней неподвижного объемного экситона; Ry = μe4 /(2ε02h2 ) – экситонный ридберг; энергии размерного квантования трансляционного движения экситона h2knl2 / 2M получаются из (2.4) путем замены m*→M. Из (2.11)

видно, что экситонное состояние описывается удвоенным набором квантовых чисел, одна половина которых относится к относительному, а другая – к его трансляционному движению. Другой важной особенностью задачи об экситоне в квантовой точке является то, что энергии размерного квантования определяются суммарной массой электрона и дырки M. Легко показать, что волновые функции и энергии экситона в квантовых точках в форме прямоугольного параллелепипеда и цилиндра могут быть получены из (2.11), если для волновых функций трансляционного движения и энергий размерного квантования использовать выражения (2.5) и (2.6), в которых должна быть проведена замена m*→M.

24

ГЛАВА 3. ПРОБЛЕМЫ ТЕХНОЛОГИИ КВАНТОВОРАЗМЕРНЫХ СТРУКТУР

Прогресс в экспериментальном изучении физических свойств квантоворазмерных структур тесно связан с развитием технологии их получения и в значительной мере им и определяется. Изготовление квантово-размерных структур в большинстве случаев требует создания полупроводниковых гетеропереходов с необходимыми свойствами. Для этого, прежде всего, необходимо подобрать подходящую пару полупроводниковых материалов. Выбор этих материалов зависит от типа структуры, которую необходимо получить. Для создания структур с двумерным электронным газом на основе гетеропереходов основным условием является требование равенства постоянных решетки у обоих полупроводников. Нарушение этого условия может привести к образованию высокой плотности дислокаций несоответствия вблизи гетерограницы, что резко ухудшает свойства переходов и делает невозможным наблюдение эффектов размерного квантования.

Гетеропереход GaAs-AlxGa1-xAs наиболее часто используют для изготовления квантово-размерных структур. Эти материалы обладают хорошим согласием решеток при любом составе твердого раствора и потому позволяют создавать гетеропереходы с различными разрывами зон на границе. Среди полупроводников класса A3B5 есть еще несколько

идеальных гетеропар, например InP-In0.53Ga0.47As, но они обладают согласием решеток лишь при одном фиксированном составе и потому не

позволяют варьировать ЕС и ЕV. Другие классы полупроводников реже используются для изготовления квантовых гетероструктур.

Одно из главных требований к технологии изготовления квантовых гетероструктур связано с необходимостью получения очень резких гетеропереходов с переходным слоем промежуточного состава, имеющим толщину всего в несколько постоянных решетки. Как видно из рис. 3.1, для плавного перехода образуется потенциальная яма большой ширины, что уменьшает расстояние между уровнями Еn и затрудняет наблюдение квантовых размерных эффектов.

Рис. 3.1. Потенциальный профиль края зоны проводимости для резкого (а) и плавного (б) гетеропереходов.

25

Другим важным требованием к технологии является возможность получения сложных профилей состава и легирования. При изготовлении сверхрешеток необходимо строго периодически менять состав растущего слоя, причем период изменения может составлять лишь несколько десятков ангстрем. При выращивании δ-слоев и структур с модулированным легированием необходимо со столь же высокой точностью менять концентрацию легирующих примесей.

Далеко не всякая эпитаксиальная технология удовлетворяет приведенным требованиям. Плохо пригодными, в частности, оказываются наиболее распространенные методики газотранспортной и жидкостной эпитаксии. Получение сложного профиля состава и легирования наталкивается на ряд технических трудностей, а сравнительно высокая температура роста вызывает диффузионное размывание гетерограницы, не позволяя получать очень резкие границы.

В настоящее время наиболее часто для изготовления качественных гетероструктур применяют метод молекулярно лучевой эпитаксии. Другим возможным способом изготовления гетероструктур является газовая эпитаксия из металлоорганических соединений. Она не требует столь сложного и дорогого оборудования, обладает меньшими возможностями контроля и управления, но, тем не менее, позволяет растить гетеропереходы требуемой резкости и структуры достаточно сложного профиля, включая сверхрешетки, квантовые нити и точки.

Получение одно- и нульмерных структур возможно путем выделения их с помощью литографии. Однако это требует применения особых методов литографии – нанолитографии, поскольку столь малые структуры трудно приготовить при помощи стандартных методов.

Значительные успехи были достигнуты в изготовлении квантовых точек и квантовых нитей с использованием эффектов самоорганизации упорядоченных наноструктур на полупроводниковых подложках. Этот метод предъявляет специфические требования к материалам гетеропары.

26