Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Университет им. Н.И. Лобачевского

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ЛЕКЦИИ_ПО_ВЫСШЕЙ_МАТЕМ_Голубев

.pdf

Скачиваний:

Добавлен:

27.03.2015

Размер:

4.74 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2612 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

, x 0;

2х 2

4х

1 x

. Итак f '(x)

х2 )2

x2 )

4х2

2|x|(1

, x 0.

1 x

4. y= 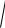1 tg2 x tg4 x .

	1	1		1	4tg3x	1
Решение y'(x)			2tgx				.
Решение y'(x)		tg2x tg4x)1/2	2tgx	cos2 x			.
	2 (1	tg2x tg4x)1/2		cos2 x		cos2 x

5. y=ln arctg						1

				1 х
			y'					1								1								1
Решение.																									.
Решение.							arctg					1				1			2			(1 x)2			.
											1 x			1
											1 x			1
																1 x

6. y=x10 х
																					1
Решение.			y' 10							х x 10					x	ln10					1
															x


																		2					x
7. у=	1	arctg			2x					1


3								3

Решение.			y'				1					1					2	3		.
Решение.			y'									2x 1 2								.
						3			1			2x 1 2						3


													3
													3

8. y=xsin x.

Решение. ln y=sin x ln x, 1у y' cosx ln x sin x 1x , y' xsin x (cosx ln x sin x 1x ) .

9. y=x1/x.
Решение. ln y=(1/x)ln x,	1	y'	1	ln x	1	1	(1 ln x) ,
			x2		x2	x2
	у

y' x1/ x 2 (1 ln x) .

10. y=x3ex2sin2x.

Решение.

ln y=3ln x+x2+ln sin2x,

y' 3

cos2x 2 ,

sin2x

2cos2x

y'=x3ex sin2x

sin2x

11.

y=logxa,

ln a

ln x

Решение. ln y=ln lna-ln lnx,

y' logx a

xln x

12.

Найти y'(x), если

х2

а2

Решение:

2х

2yy'

0 ,

2yy'

2 b2 x

y'(x)=

b2x

; y=

b2 (1

) ,

а2

y'(x)

b2 x

b2 (1 x2 a2 )

13.

Найти y' , если имеет место равенство 2y lny=x.

Имеем: 2y'ln y+2y'=1, y'=

, где у=у(х) определяется уравнением

2(1 ln y)

вида 2y ln y=x.

14.

y=x ex2, найти y''(x).

Решение: y'=ex2+x ex2 2x,

y''=ex2 2x+ex2 2x+2x2 ex2 2x+2x ex2=2ex2(3x+2x3).

15.

y=ln(ax+b). Найти yIV.

y'=

a ;

y''=

a2 ;

y'''=

2а3

;

yIV=

2 3а4

(ax b)

(ax b)2

(ax b)3

(ax b)4

16.

Найти yx'', если x=a t2, y=b t3.

3bt

t ,

:2at

2at

xх

17.

Найти yx''', если x=a cos t,

y=b sin t.

b cos t

ctgt ;

a sin t

yx t

a sin t b

;

x›

x t

a sin 2 t

a 2 sin 3 t

3sin

t cos t

3b cos t

a sin t

x t

sin 6 t

sin 5 t

Лекция 14

ДИФФЕРЕНЦИАЛ ФУНКЦИИ.

1. Основные понятия.

Как было показано, функция f(x), имеющая производную в точке х, имеет в этой точке приращение f=f

(x) x+o( x).

Определение. Дифференциалом функции у=f(x) в данной точке х, отвечающим приращению аргумента

х, называется число

dy f '(x)dx . Здесь по определению полагаем, что

dx= x.

Очевидно, что dy y.

Определение. Линейная часть приращения f функции f(x) относительно х называется дифференциалом функции.

Т.е. если у=yx x+o( x), то dy=yx dx.

Геометрическая интерпретация.

а)

б)

Здесь у=х2

		Здесь	у=х2
	y=2x x+ x2,	у=АС,
	dy=2x dx.		dy=AB.
	Замечание. Из рисунка б) следует, что дифференциал функции f(x) в точке х, равен приращению
ординаты касательной к кривой у =f(x)		в точке (x; f(x)) , которое вызвано приращением аргумента х.
	2. Правила дифференцирования.
	Из определения дифференциала следует: если некоторая функция f(x)		имеет в точке х производную, то
она в той же точке имеет дифференциал.
Очевидна таблица дифференциалов некоторых функций.
y=c;	dy=0
y=x ;	dy= x -1 dx

y=1/x; dy= dx

x ;

dy=

y=ax;

dy=axln a dx

y=ex;

dy=exdx

y=logax;dy=1/x logae dx

y=ln x;

dy=1/x dx

y=sin x; dy=cos x dx

y=cos x; dy=-sin x dx

y=tg x;

dy=

cos2 x

y=ctg x; dy=

sin2 x

y=arcsin x;

dy=

1 х2

y=arccos x;

dy=

1 х2

y=arctg x;

dy=

1 х2

y=arcctg x;

dy=

1 х2

Правила дифференцирования.

d(c u)=c du, так как fx=c ux; d(c u)=c uxdx=c du. d(u v)=du dv, т.к. (u v)=u v , d(u v)=(u v )dx=du dv. d(u v)=udv+vdu, т.к. (uv)=u v+uv , d(u v)=uv dx+u vdx=udv+vdu.

vdu udv

u v uv

d(u/v)=

, т.к.

3. Инвариантность формулы первого дифференциала.

Помним, что дифференциал функции y=f(x) имеет вид: dy=f (x)dx, где х - независимая переменная.

vdu udv

Докажем, что это представление дифференциала не изменится и в случае, когда аргумент х является функцией х=(t) переменной t, где - дифференцируемая функция.

Свойство первого дифференциала сохранять свою формальную запись называется инвариантностью его

формы.

Итак, если аргумент х есть функция (t), то функцию f(x) можно рассматривать как сложную функцию переменной t, т.е. y=f[ (t)]; здесь t - является независимой переменной.

В этом случае запишем дифференциал y(t):

dy={f( (t))}t dt, т.е dy=f (x) (t) dt, а так как (t)dt=dx, то dy=f (x)dx. Что и требовалось доказать.

4. Приложения первого дифференциала.

Предположим, что нам задана дифференцируемая функция f(x), x X. Известно, что f df. Тем не менее с

точностью до бесконечно малой более высокого порядка малости, чем х , при х0, справедливо приближенное равенство: уdy

Абсолютная погрешность вычисления имеет вид: | y-dy|=|о( x)|

| y dy|

Назовем относительной погрешностью вычисления величину: .

Относительная погрешность будет бесконечно малой при х0, т.к.

lim	\| y dy\|	=	lim
	y
x 0			x 0

y	x o( x) y x
x	x	=0.

y x o( x)

Часто замена приращения функции ее дифференциалом применяется для вычисления значения функции в какой-либо точке. А именно , если у=f(x+ x)-f(x), тогда при уdy, имеем dy f(x+ x)-f(x), откуда

f (x)dx f(x+ x)-f(x) и f(x+ x) f(x)+f (x)dx.							(*)
Эта формула справедлива с точностью до величины о(х)							в любой точке существования производной
функции f(x).
Следует помнить, что формула (*) применяется при достаточно малых значениях х.
Пример 1. Вычислить sin29
Рассмотрим функцию y=sin x, так как			sin(x+ x) d(sin x)+sin x, то
	2			2
sin(30 -1 ) cos30 (-		)+sin30 (здесь х=-1 =-			,	х= 6 ),	и
	360			360

sin29	1					3			1	0,015 0,485
sin29										0,015 0,485
2				180		2		2
	Пример 2. Доказать формулу:												а2 х а+x/2a, a>0.
Для этого рассмотрим функцию f(x)=												а2 х		в окрестности точки х=0 и вычислим это значение по
приведенной выше формуле, полагая
х0=0, х=х-х0=х.
											1							1
		а	2		х						1				а	2	х	1
			2													2
Имеем							f (0) x+f(0);				f (0)= 2а и							a+ 2а	x.
Имеем							f (0) x+f(0);				f (0)= 2а и							a+ 2а	x.

												4		.
			Пример 3. Вычислить значение									4	80	.
						4					, где х=81; х=-1. Тогда 4					( 4		) x+ 4		. 4		(-
Рассмотрим функцию						4		х х			, где х=81; х=-1. Тогда 4				х х	( 4	х	) x+ 4	х	. 4	80	(-
1)	1			+3=3-		1				2,991

	4						4 27
	4		3				4 27
4		х			х 81		5. Дифференциалы высших порядков.
							5. Дифференциалы высших порядков.
								ым	дифференциалом функции f(x) в точке х, первый дифференциал от (n-1)														ого
			Будем называть n
дифференциала, то есть
					dny=d(dn-1y).
			Замечание. Если аргумент х является независимым переменным или линейной функцией некоторой
переменной t , то имеем (по определению первого дифференциала): d2y=f (x)(dx)2.
			Замечание. Если аргумент х									является зависимой переменной (нелинейной), то

d2y=d(dy)=d(fx dx)= f (x)(dx)2	f (x)d2x .
	x

Отсюда следует, что форма второго дифференциала, а следовательно и дифференциалов высших порядков не является инвариантной.

Дифференциалы высших порядков функций заданных параметрически.

'(t)

Пусть функция у=f(x) задана параметрически у= (t);

x= (t). Тогда

ух =

и dy= dt;

dx= dt, ух = '(t) .

'(t)

Значит dy= '(t) dx.

Аналогично вычислим (по определению) дифференциал второго порядка:

'(t)

t : '(t)

(dx)

x .

'(t)

Очевидно можно вычислить подобным образом дифференциалы порядков более второго.

Формула Лейбница.

d n (u v)	n		d n i u di v ,
	Ci
	i	n
		0
где d0u=u; d0v=v, а функции u(x)		и v(x) имеют дифференциалы nого порядка.

						6. Примеры.
1.	Найти	y	, если y=u2; u=u(x).
		xx
y =2u ux ;		y =2ux ux +2u u
				xx
2.	Найти y , y, если y=f(x2).
y =f 2x, y =f 2x 2x+f 2,				y =f 2x 2x 2x+f 4 2x+2f 2x.
3.	Вычислить dy и d2y, если y=vu; где u=u(x), v=v(x).
dy=du v+udv, d2y=d2u v+du dv+du dv+u d²v.
d2y=u (dx)2 v+2ux vx (dx)2+u					v	(dx)2.
					xx
4.	Вычислить d2ex, если			1)	х - независимая переменная,

2) х - зависимая переменная.

1)d2ex=ex(dx)2;

2)dex=ex dx, d2ex=ex(dx)2+exd2x.

5.Вычислить d5y, если y=x5.

d5y=5!(dx)5

6. Вычислить d4y, если y=eu, u= (t).

dy=eudu, d2y=eu(du)2+eud2u, d3y=eu(du)3+eud3u+eu2du d2u+eudu d2u, d4y=eu(du)4+eu 3(du)2d2u+eu3(du)2d2u+3eu(d2u)2+3eudu d3u+eudu d3u+eud4u.

Найти дифференциал n -ого порядка.
7. y=excos x
		n
d n y ex	Cin (cosx)					(i) dxn		(смотри формулу Лейбница).
i 0
8. y=1/x.
d ny ( 1)n			n!		dxn.

			xn 1
			xn 1
9. y=ax.
dn ax ax lna n dxn .
10. y=ln x.
dn(ln x)= 1		n 1		1 2 (n 1)
dn(ln x)= 1							dxn.

11. y=xm, m>n, m N.

dn(xm) =m(m-1)...(m-n+1) xm-ndxn. 12. y=xm (m<n).

dn(xm) =0.

13. y=xm (m=n). dn(xm)=n!dxn.

Лекция 15 ОСНОВНЫЕ СВОЙСТВА ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЙ.

1. Монотонность функции.

Определение. Функция у=f(x) называется возрастающей (убывающей) в точке х=х0, если существует окрестность |x-x0|< точки х0, в пределах которой f(x)<f(x0) при x<x0 и f(x)>f(x0) при x>x0. (f(x)>f(x0) при x<x0 и f(x)<f(x0) при x>x0).

Функция является монотонной на множестве Х, если она монотонна в каждой точке этого множества.

Теорема. Достаточное условие монотонности функции.

Если функция y=f(x) дифференцируема в точке х0 и f (х0)>0 (f (x0)<0), то функция у=f(x) возрастающая

(убывающая) в точке х=х0.
Доказательство. По определению производной в точке х0							имеем
f (x0)= lim	f (x) f (x0 )				f (x0)>0 (для монотонного возрастания функции).
		. Тогда положим, что

x x0	х х0
		f (x) f (x		0	)	, x x0	;

			x x0
Рассмотрим функцию (х)=
			f '(x0 ),			x x0.

Указанная функция непрерывна в некоторой окрестности точки х0, т.е. при х (х0- , х0+ ). Поэтому, в силу сохранения знака непрерывной функции, существует окрестность (х0- 1, х0+ 1), 1< , в которой функция

	f (x) f (x0 )
(x)>0, т.е.		>0 при х (х0- 1, х0+ 1).

	х х0

Откуда следует, что f(x)<f(x0) при х<x0 и f(x)>f(x0) при x>x0. Последнее означает, что в точке х=х0 функция y=f(x) возрастающая.

Замечание. Условие возрастания (f (x0)>0) функции f(x) в точке х0 не является необходимым, а только достаточным.

Например. Функция у=х3 всюду монотонно возрастающая, хотя при х0=0 f (0)=0.

2. Локальный экстремум функции.

Определение. Точка х=х0 называется точкой локального максимума (минимума), если существует окрестность |x-x0|< точки х0 такая, что имеют место неравенства f(x) f(x0) х (х0- , х0+ ),

(f(x) f(x0) х (х0- , х0+ )).

Точки локального максимума и минимума объединяются общим термином -локальный экстремум. Замечание. Здесь мы предполагаем, что точка х0 является внутренней точкой области определения

функции f(x), а сама функция непрерывной.

Теорема (Ферма). Необходимое условие экстремума.

Если функция у=f(x) дифференцируема в точке х=х0 и имеет в точке х0 локальный экстремум, то f (x0)=0. Доказательство. Пусть функция у=f(x) в точке х=х0 имеет экстремум. Тогда (по определению

экстремума) в этой точке функция не может ни убывать ни возрастать, т.е. не может быть ни f (x0)<0, ни f (x0)>0. Остается единственное: f (x0)=0.

Замечание. Точки, в которых производная f (x) обращается в нуль называются стационарными. Замечание. Доказанное условие локального экстремума является лишь необходимым. Действительно, если

рассмотреть функцию у=х3, то f (0)=0, но в точке х0=0 функция у=х3 экстремума не имеет.

3. Теоремы о среднем.

Теорема (Ролля). Если функция у=f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (a, b) и кроме того f(a)=f(b), то найдется точка (a, b) такая, что f ( )=0.

Доказательство. Так как у=f(x) непрерывна на [a, b], то на промежутке [a, b] эта функция достигает наибольшего и наименьшего значения m и М (теорема Вейерштрасса). Рассмотрим два случая:

1. m=M. В этом случае f(x)=const и f (x) 0.

2. M>m. В этом случае функция достигает наибольшего или наименьшего значения во внутренней точке , т.е(a, b). Это следует из того, что f(a)=f(b), и одновременно f(x) не может достигать наибольшего и наименьшего значений на концах отрезка.

Таким образом в точке х= функция достигает экстремума, причем в точке	х= существует производная	f ( ).
В силу теоремы Ферма необходимо f ( )=0.

Геометрический смысл.

В точке х=х0 касательная к графику функции параллельна оси Ох.

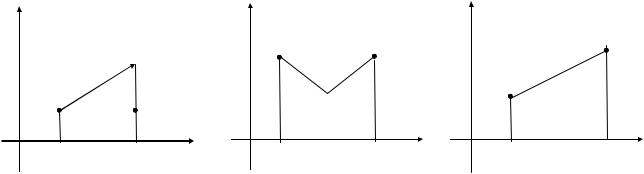
Все три условия теоремы существенны, т.е. при невыполнении одного из них теорема не имеет места. Поясним примерами:

0	а	b	x 0 a	b	x	0	a	b	x
функция разрывна			функция				f(a) f(b)
			не дифференцируема.

Замечание. Точка (a, b) может быть не единственной. Теорема (Лагранжа).

Пусть 1) функция f(x) определена и непрерывна на отрезке [a, b];

2) f(x) дифференцируема на (a, b).

Тогда найдется точка (a, b) такая, что справедлива формула f(b)-f(a)=f ( ) (b-a).

Доказательство. Рассмотрим вспомогательную функцию

F(x)=f(x)-f(a)-	f (b) f (a)	(x-a).

	b a
	b a

Для функции F(x) выполнены все условия теоремы Ролля: непрерывность, дифференцируемость и F(a)=F(b). Т.е. существует т. (a, b) такая, что F ( )=0.

F (x)=f (x)-	f (b) f (a)	,	F ( )=f ( )-	f (b) f (a)	=0,	f(b)-f(a)=f ( )(b-a).
	b a			b a

Последнее равенство часто называют формулой Лагранжа.

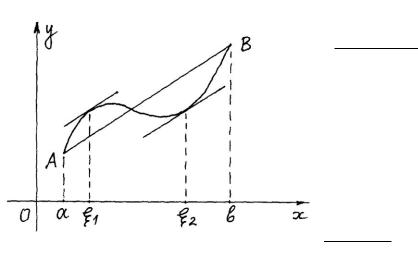
Геометрический смысл.

Так как угловой коэффициент секущей АВ равен

f (b) f (a)

, то теорема Лагранжа утверждает:

b a

на дуге АВ найдется точка, в которой касательная к ней параллельна хорде АВ

b) f (a)

b a

f(x+ x)-f(x)=f ( ) x - формула конечных приращений, f(x0+ x)-f(x0)=f (x0+ x) x, (0, 1).

3) Теорема Ролля является частным случаем теоремы Лагранжа.

4. Следствия из теоремы Лагранжа.

Теорема. Для того чтобы дифференцируемая на (a, b) функция f(x) была постоянной, т.е. f(x)=const, необходимо и достаточно чтобы имело место равенство f (x)=0 при любом х(a, b).

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2612 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
27.03.20151.1 Mб125Лекции-История и методология языкознания.doc
#
03.05.2015366.08 Кб154Лекции-ст.doc
#
13.08.201973.73 Кб7Лекции.doc
#
09.11.20184.19 Mб46лекции.doc
#
27.03.2015223.47 Кб36Лекции.docx
#
27.03.20154.74 Mб73ЛЕКЦИИ_ПО_ВЫСШЕЙ_МАТЕМ_Голубев.pdf
#
27.03.2015274.94 Кб7Лекции_по_ИЭ_2.doc
#
11.03.20162.17 Mб26Лекции_тервер.pdf
#
27.03.20153.81 Mб123ЛекцииМО.doc
#
27.03.2015473.6 Кб10Лекционный курс для подготовки (студентам).doc
#
27.03.2015222.15 Кб17Лекция 02 Кинематика криволинейного движения..pdf