Пример:

Необходимо определить сумму простого процента за год при следующих условиях: первоначальная сумма вклада — 1000 усл. ден. ед.; процентная ставка, выплачиваемая ежеквартально — 20%.

Подставляя эти значения в формулу получим сумму процента: 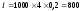усл. ден. ед.; будущая стоимость вклада в этом случае составит:

S = 1000 + 800 = 1800 усл. ден. ед.

Множитель (1 + ni) называется множителем (или коэффициентом) наращения суммы простых процентов. Его значение всегда должно быть больше единицы.

Процесс наращения суммы вклада во времени по простым процентам может быть представлен графически (рис. 10.9).

P

Рис. 10.9. График наращения суммы денежных средств

по простым процентам (при процентной ставке 20%)

Пример:

Необходимо определить сумму дисконта по простому проценту за год при следующих условиях: конечная сумма вклада определена в размере 1000 усл. ден. ед.; дисконтная ставка составляет 20% в квартал.

Подставляя эти значения в формулу расчета суммы дисконта, получим:

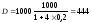усл. ден. ед.

Соответственно настоящая стоимость вклада, необходимого для получения через год 1000 усл. ден. единиц, должна составить:

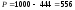усл. ден. ед.

Используемый в обоих случаях множитель 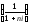называется дисконтным множителем (коэффициентом) суммы простых процентов, значение которого всегда должно быть меньше единицы.

Процесс дисконтирования суммы денежных средств может быть представлен графически (рис. 10.10).

Сумма денежных средств (усл. ден. ед)

P

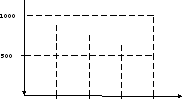
Сумма процента

P₁=889

P₂=778

P₃=667

P₄=556

Периоды платежей

1

2

3

4

0

Рис. 10.10. График дисконтирования суммы денежных потоков по простым процентам (при дисконтной ставке 20%)

Пример:

Необходимо определить будущую стоимость вклада и сумму сложного процента за весь период инвестирования при следующих условиях:

• первоначальная стоимость вклада — 1000 усл. ден. ед.;

• процентная ставка, используемая при расчете суммы сложного процента, установлена в размере 20% в квартал;

• общий период инвестирования — один год.

Подставляя эти показатели в вышеприведенные формулы, получим:

Будущая стоимость вклада усл. ден. ед.

Сумма процента = 2074 – 1000 = 1074 усл. ден. ед.

Ic (сумма процента)

Рис. 10.11. График наращения суммы денежных средств по сложным процентам

(при процентной ставке 20%)

Пример:

Необходимо определить настоящую стоимость денежных средств и сумму дисконта по сложным процентам за год при последующих условиях:

• будущая стоимость денежных средств определена в размере 1000 усл. ден. ед.;

• используемая для дисконтирования ставка сложного процента составляет 20% в квартал.

Подставляя эти значения в формулы, получим:

Настоящая стоимость =P 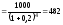усл. ден. ед.

Сумма дисконта =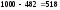 усл. ден. ед.

Графически процесс дисконтирования денежных средств по сложным процентам представлен на рисунке 10.12.