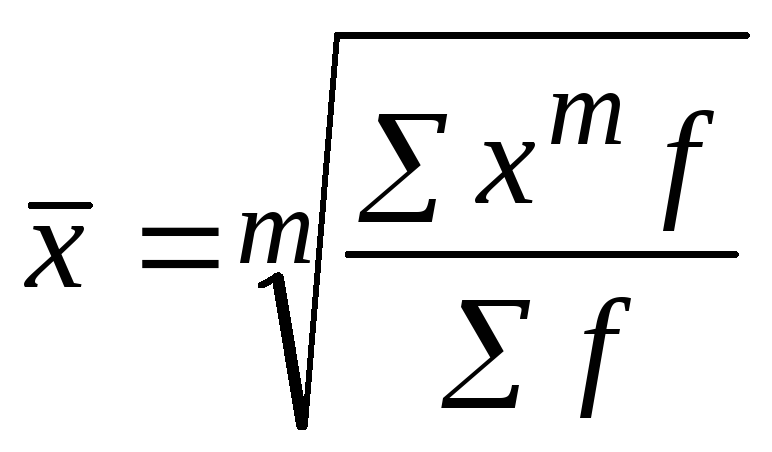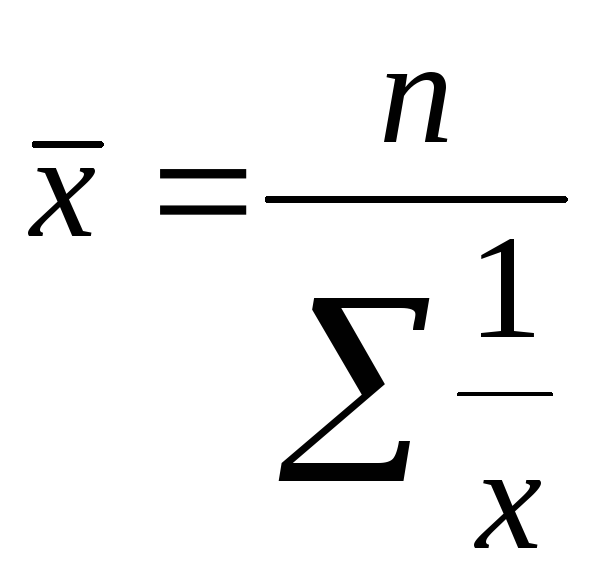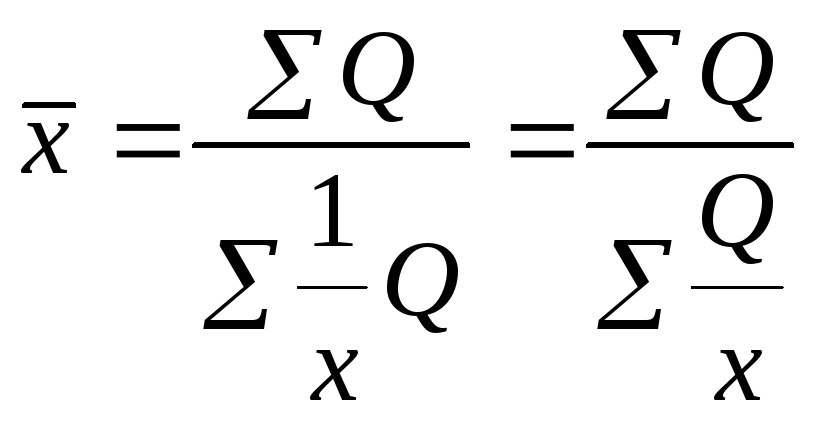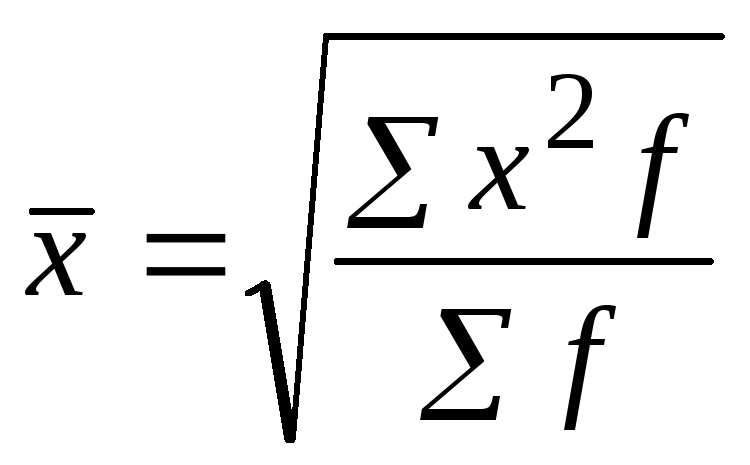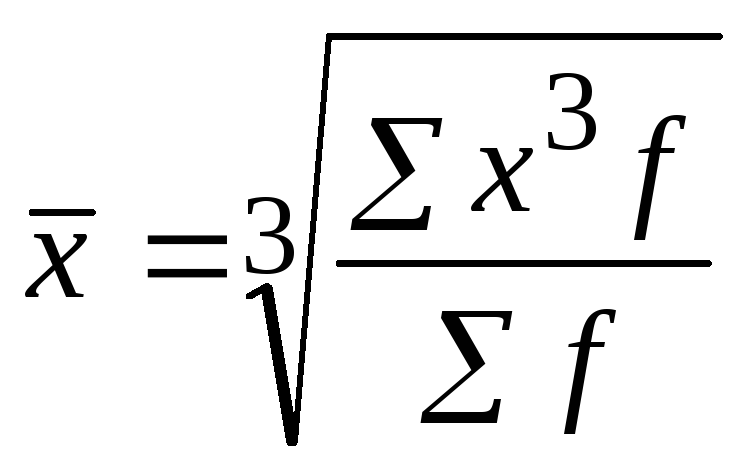- •Предмет и метод статистики
- •Основные понятия статистики
- •Виды статистических показателей
- •Этапы статистического исследования
- •III этап – расчёт обобщающих показателей с целью изучения связей, объективно существующих между социально-экономическими явлениями. Сводка и группировка данных статистического наблюдения.
- •Ряды распределения
- •Средние величины.
- •Степенные средние
- •Свойства средней арифметической
- •Структурные (описательные) средние Нахождение моды и медианы в интервальных рядах
Средние величины.
ОСРЕДНЕНИЕ УДЕЛЬНЫХ ПОКАЗАТЕЛЕЙ
Удельную величину можно представить как объёмный показатель изучаемого признака в расчёте на единицу численности среды, в которой развивается исследуемое социально-экономическое явление:
![]()
Например, ВВП на душу населения – это абсолютный ВВП, делённый на численность населения. Но оба элемента дроби не есть что-то монолитное, и обязательно состоят из каких-то структурных звеньев. Поэтому в действительности понятия удельной величины и средней здесь как бы переходят друг в друга. Тогда вышеприведённая формула приобретает несколько более сложный вид:
![]()
Эта формула называется средней агрегатной. Следует заметить, что это название редко можно встретить в учебной литературе, равно как и формулу, но на словах этот механизм описывается повсеместно.
Однако для того чтобы применить эту формулу, нужно иметь слагаемые объёма и численности. Могут быть случаи, когда исследователь располагает другими данными:
А) известны варианты удельного показателя «x» и численности «f», тогда исходя из смысла удельной величины получим:
![]()
Подставим это в формулу средней агрегатной и получим среднюю арифметическую взвешенную:
![]()
Б) известны варианты удельного показателя «x» и объёма «Q». тогда исходя из смысла удельной величины получим:
![]()
Подставим это в формулу средней агрегатной и получим среднюю гармоническую взвешенную:
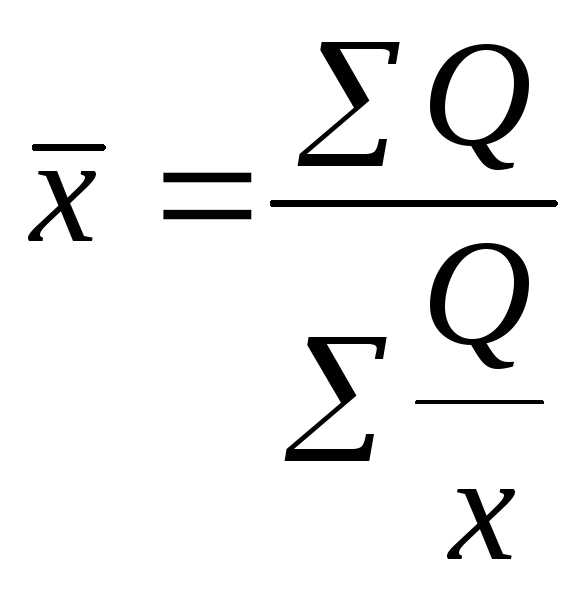
Важно заметить, что в учебной литературе в формуле средней гармонической вместо обозначения «Q» чаще применяют буквы «M» или«W».
Степенные средние
|
|
Простые (невзвешенные) |
Взвешенные |
|
Общие формулы |
|
|
|
(средняя гармоническая) |
|
|
|
(средняя геометрическая) |
|
|
|
(средняя арифметическая) |
|
|
|
(средняя квадратическая) |
|
|
|
(средняя кубическая) |
|
|
Свойства средней арифметической
|
1 |
|
Средняя величина от постоянной равна ей самой.
|
|
2 |
|
Произведение средней арифметической на сумму частот (весов) равно сумме произведений вариант на их частоты (веса)
|
|
3 |
|
Если к каждой варианте прибавить постоянную величину, то средняя изменится на это же число
|
|
4 |
|
Если каждую варианту умножить на постоянную величину, то средняя изменится на эту же величину.
|
|
5 |
|
Если каждую частоту умножить на постоянную величину, то средняя не изменится.
|
|
6 |
|
Алгебраическая сумма отклонений вариант от их средней арифметической равна нулю
|
|
7 |
|
Сумма квадратов отклонений вариант от их средней арифметической меньше, чем от любого другого числа.
|
|
8 |
|
Сумма средних равна средней сумме. |
Структурные (описательные) средние Нахождение моды и медианы в интервальных рядах
Мода:
![]() ,
где:
,
где:
![]() -
начало (нижняя граница) модального
интервала, т.е. интервала с максимальной
численностью (
-
начало (нижняя граница) модального
интервала, т.е. интервала с максимальной
численностью (![]() );
);
![]() -
величина модального интервала;
-
величина модального интервала;
![]() -
частоты (веса) интервалов (численности
групп), соответственно: предшествующего
модальному, модального, следующего за
модальным.
-
частоты (веса) интервалов (численности
групп), соответственно: предшествующего
модальному, модального, следующего за
модальным.
Медиана:
![]() где:
где:
![]() -
начало (нижняя граница) медианного
интервала, т.е. интервала, в котором
находится единица совокупности с номером
-
начало (нижняя граница) медианного
интервала, т.е. интервала, в котором
находится единица совокупности с номером
![]()
![]() -
величина медианного интервала;
-
величина медианного интервала;
![]() -
частота, накопленная до медианного
интервала;
-
частота, накопленная до медианного
интервала;
![]() -
частота (численность) медианного
интервала.
-
частота (численность) медианного
интервала.