Аналитическая геометрия

Задание линии в плоскости

Пусть {О, } – аффинная система координат в плоскости.

О. Геометрическое место точек M (x, y), координаты которых удовлетворяют уравнению F(x,y) = 0, называется линией в плоскости, а уравнение F(x,y) = 0 – уравнением линии в плоскости.

Если F(x,y) – многочлен n-й степени, то линия называется алгебраической n-го порядка.

Прямая в плоскости

Пусть - декартова система координат.

Т1 ( О задании прямой в плоскости )

Всякая прямая в плоскости задается уравнением Ax + By + C = 0 (1), где

A² + B² > 0. Всякое уравнение (1) задает прямую в плоскости.

Следствие. Уравнение прямой в плоскости задается с точностью до постоянного множителя.

Т2 ( о взаимном расположении 2-х прямых )

Пусть - две прямые. Тогда :

Способы задания прямой в плоскости

1. Каноническое уравнение : , где- координаты направляющего вектора прямой,- координаты точки на прямой.

2. Параметрическое уравнение : , гдеt – параметр

3. Уравнение в отрезках :

4. Уравнение прямой в отрезках : 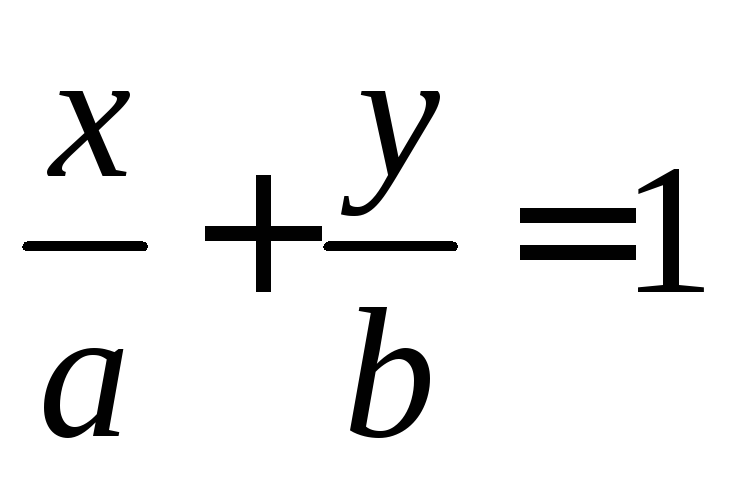, гдеa, b – отрезки, отсекаемые прямой на осях координат.

5. Нормальное уравнение : , где-угол между нормалью к прямой и осью x, p – расстояние от начала координат до прямой.

Задание поверхности в пространстве

Пусть {О, } – аффинная система координат в пространстве.

О. Геометрическое место точек M (x, y,z), координаты которых удовлетворяют уравнению F(x,y,z) = 0, называется поверхностью в пространстве, а уравнение F(x,y,z) = 0 – уравнением поверхности в пространстве.

Если F(x,y,z) – многочлен n-й степени, то поверхность называется алгебраической поверхностью n-го порядка.

Плоскость в пространстве

Пусть - декартова система координат в пространстве.

Т1 ( О задании плоскости в пространстве )

Всякая плоскость в пространстве задается уравнением Ax + By + Cz +D = 0 (1), где A² + B² + C² > 0. Всякое уравнение (1) задает плоскость в пространстве.

Следствие. Уравнение плоскости в пространстве задается с точностью до постоянного множителя.

Т2 ( о взаимном расположении 2-х плоскостей )

Пусть

Тогда :

Способы задания плоскости в пространстве

1. Уравнение плоскости, проходящей через 3 заданные точки

2. Уравнение плоскости в отрезках

, где a, b, c – отрезки, отсекаемые плоскостью на координатных осях.

3. Нормальное уравнение плоскости

, где - направляющие косинусы нормали к плоскости,p – расстояние от плоскости до начала координат.

Прямая в пространстве

О. Прямая в пространстве – геометрическое место точек M( x, y, z), координаты которых удовлетворяют системе уравнений :

(*) – общее уравнение прямой

Способы задания прямой в пространстве

1. Каноническое уравнение прямой : , где- координаты направляющего вектора, а- координаты точки

2. Параметрическое уравнение прямой :, получаемое из канонического введением параметраt.

3. Уравнение прямой, проходящей через 2 заданные точки

Кривые 2-го порядка

Рассмотрим основные типы кривых 2-го порядка.

Эллипс

Эллипс ( Э ) - геометрическое место точек М на плоскости, сумма расстояний которых до двух заданных точек F₁ и F₂ постоянна

Точки F₁ и F₂ называются фокусами Э. Предполагается что ,где.

Если выбрать систему координат так, чтобы ось абсцисс проходила через фокусы, а ось ординат – через середину расстояния между фокусами, то уравнение Э запишется в виде

Свойства Э:

1. Ограниченность -

2. Симметрия относительно координатных осей и начала координат.

3. Эксцентриситет Э - параметр, характеризующий вытянутость Э.

4. Директрисы Э – прямые Δ, заданные уравнением: .

Директориальное свойство Э:

Пусть точка ,r- расстояние от М до фокуса , d – расстояние от М до директрисы. Тогда