4. Производная неявной функции

Определение 2. Если функция у = f(x), определенная на некотором интервале (а; b), такова, что уравнение F(x; y) = 0 при подстановке в него у = f(x) обращается в тождество относительно х, то функция y = f(x) называется неявно заданной уравнением F(x; y) = 0.

Чтобы найти производную неявной функции у по аргументу х, заданной уравнением F(x; y)=0, необходимо продифференцировать левую и правую части этого уравнения, считая у функцией от х . Из полученного линейного уравнения находим искомую производную.

Пример 3. Вычислить производную неявной функции.

x² + x²y + y²x + y² + 3 = 0.

Решение

2x + 2xy + x² 2y= 0

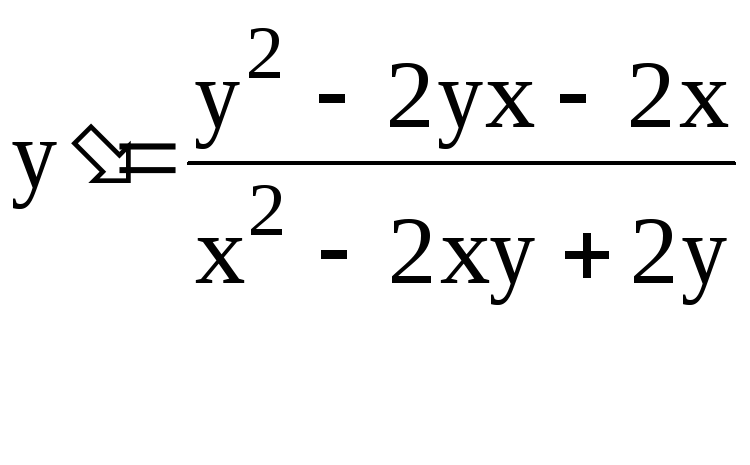
Вычислить производные неявных функций

75. x³ + y³  3xy = 0 76. x² + y² = 4

77. x⁴  6x²y² + 9y⁴ = 100 78. Ax² + 2Bxy + Cy² = F

79. x sin y + y sin x = 0 80. e^x + e^y  2xy  1 = 0

81. 82. x² sin y + y² cos x = 0

83. 84. е^у/х  e^x/y = 1

85. x^y + y^x = 0 86. + y² ln x = 4

5. Производные высших порядков

Определение 3. Производная называется производной первого порядка.

Производная от называется производной второго порядка или второй производной от функции f(x) и обозначается,,

или .

Производная от называется производной третьего порядка или третьей производной от функции f(x) и обозначается,,

или и т.д.

Производная n-го порядка есть производная от производной (n-1)-го порядка, т.е. .

Пример 4. Найти производную второго порядка от функции

у=.

Решение

Найти производные второго порядка от функций:

87. у = tg x 88. y = ctg x

89. y = sin²x 90. y = cos²x

91. y = 92. y = ln (2x3)

93. y = x sin x 94. y =

95. y = 2^x 96. y = e^1/x

97. y = x² ln x 98. y = a^x x³

99. 100. y = ln

6. Правило Лопиталя Устранение неопределенностей вида ,

Правило Лопиталя. Если функции f(x) и g(x) дифференцируемы в некоторой окрестности точки x₀ за исключением, быть может самой точки x₀, причем, в этой окрестности и, если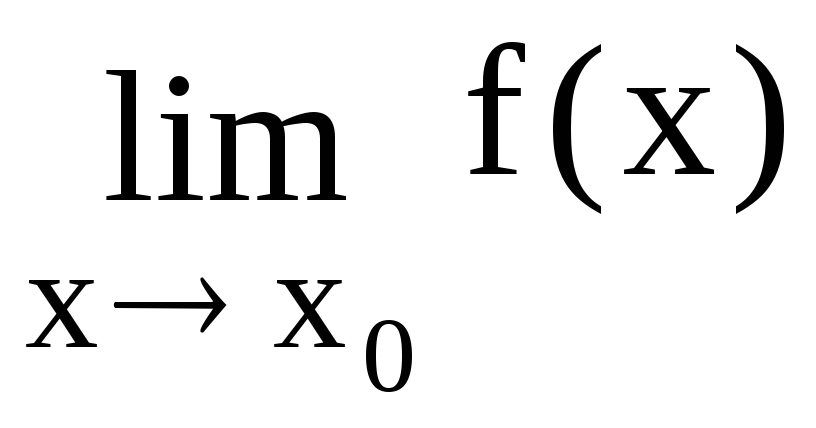==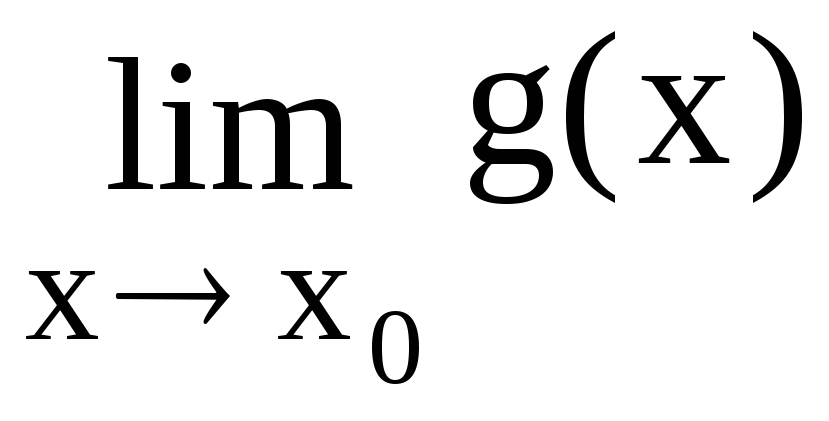 0 или==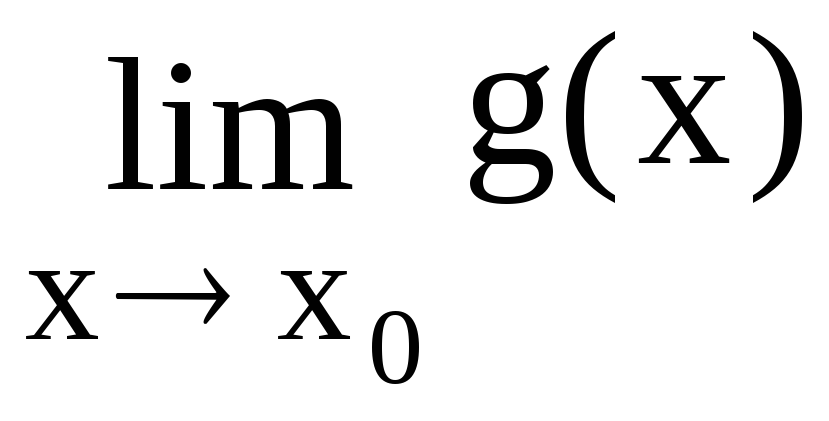 , то

,

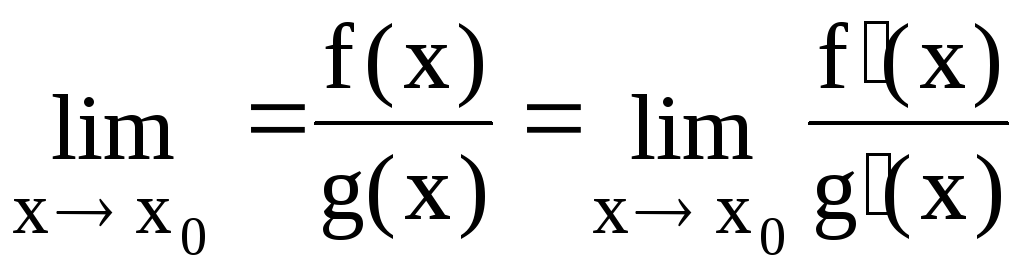если последний предел существует.

Иными словами, для неопределенностей вида илипредел отношения двух функций равен пределу отношения их производных, если последний существует (конечный или бесконечный).

Здесь x₀ может быть числом, +, либо.

Пример 5. Вычислить предел .

Решение. Имеем неопределенность вида . Для ее устранения воспользуемся правилом Лопиталя

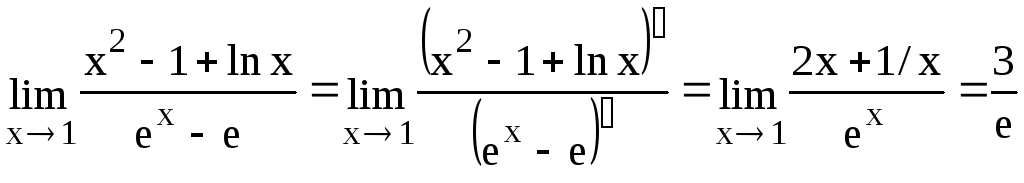
Пример 6. Вычислить предел .

Решение. Имеем неопределенность вида . Применяя трижды правило Лопиталя, получим

.

Вычислить пределы

101. 102.

103. 104.

105. 106.

107. 108.

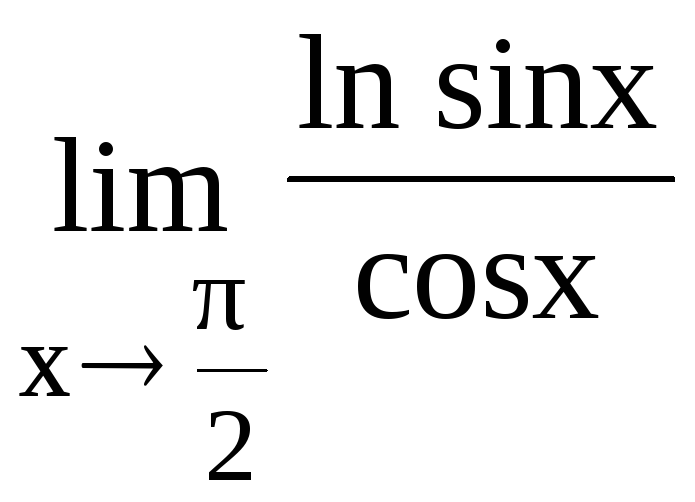
109. 110.

111. 112.

113. 114., a >1

115. 116.

117. 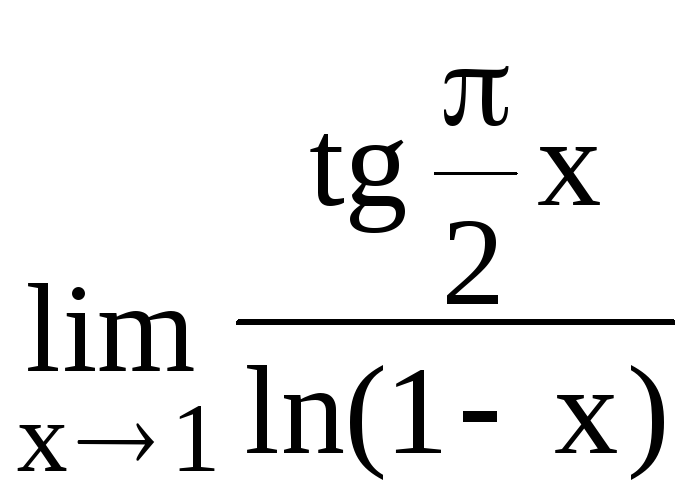118.

119. 120.

121. 122.

7. Неопределенности вида 0  , 00, 1, 0 и их устранение

Неопределенность вида 0   сводится путем алгебраических преобразований к неопределенностям вида , а затем раскрываются с помощью правила Лопиталя.

Неопределенности вида 0⁰, 1^, ⁰ с помощью тождества

f(x)^g(x)  e^{g(x) lnf(x)} сводятся к неопределенности вида 0  .

Пример 7. Вычислить предел

Решение. Имеем неопределенность вида 0. Но x ln |x| =  получена неопределенность вида . Применяя правило Лопиталя, получим=.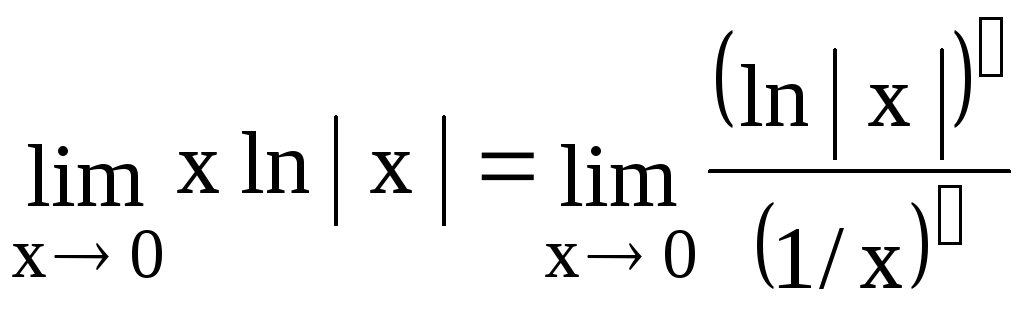

Пример 8. Вычислить предел

Решение. Имеем неопределенность вида 0⁰. Но x^x = e^{x ln x} и получаем в показателе степени неопределенность вида 0  , которая рассмотрена в предыдущем примере. Следовательно

.

Пример 9. Вычислить .

Решение. Имеем неопределенность вида 1^. Но (1 + x)^1/x = e^{1/xln(1+x)}

и в показателе степени получена неопределенность вида . Устраним ее, используя правило Лопиталя.

.

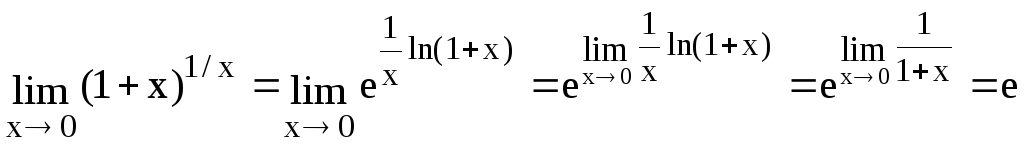Пример 10. Вычислить .

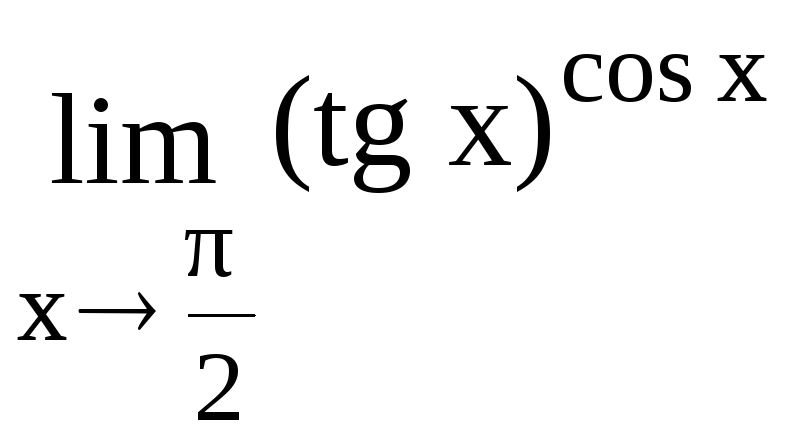Решение. Имеем неопределенность вида ⁰.

Но и в показателе степени получена неопределенность видаПрименяя правило Лопиталя, находим

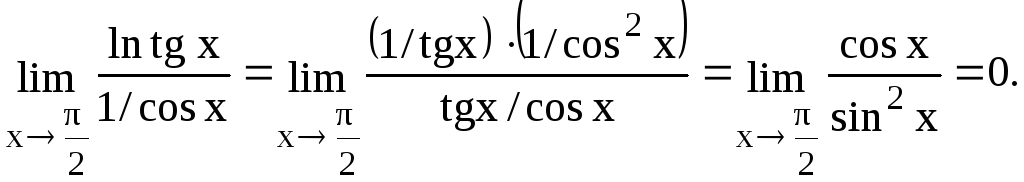
Следовательно .

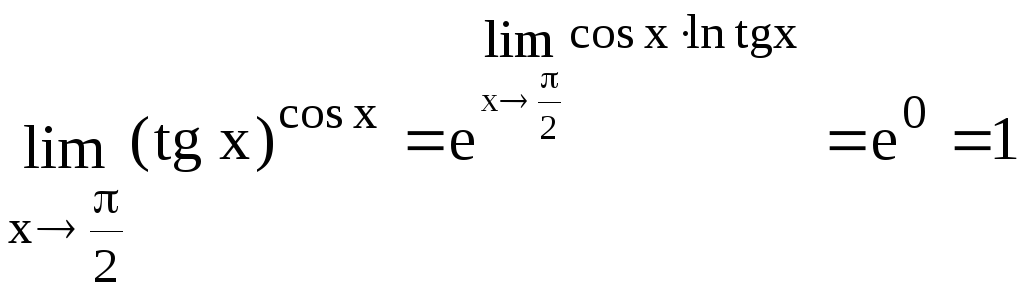Вычислить пределы

123. 124.

125. 126.

127. 128.

129. 130.

131. 132.

133. 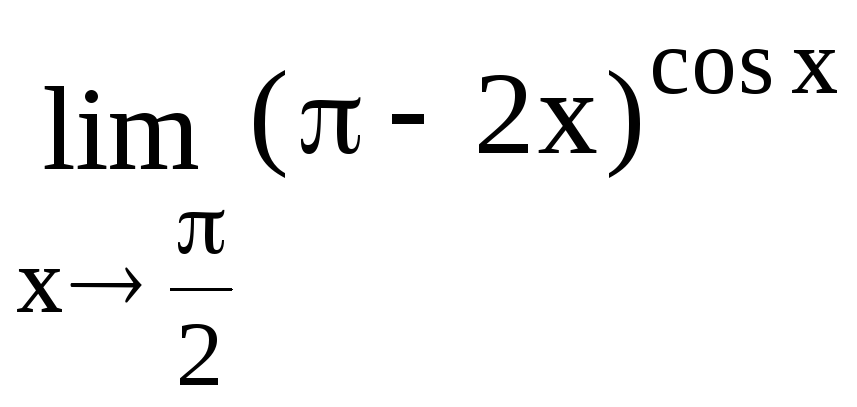134.

135. 136.

137. 138.

139. 140.

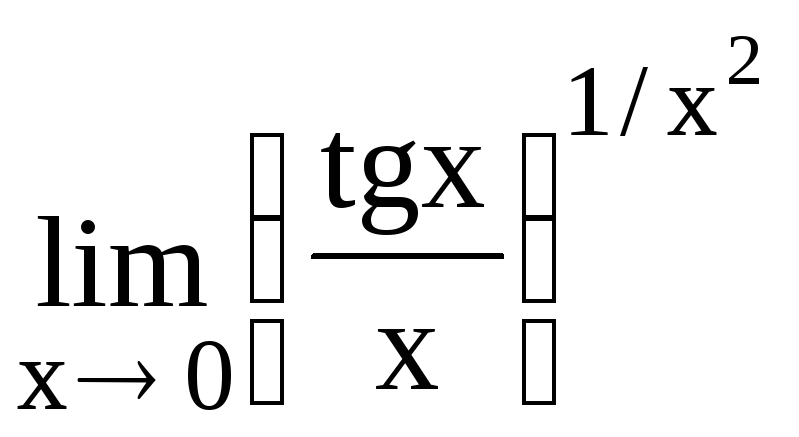141. 142.