3. Свойства степенных рядов
Пусть степенной ряд сходится к функции S(x) в области ее определения, т. е.
,
(6.10)
тогда:
1. Сумма S(x) ряда (6.10) есть функция непрерывная в области его сходимости.
2.
Если степенной ряд (6.10) сходится к функции
S(x)
для х
[a;
b],
то его можно почленно интегрировать по
любому промежутку из его области
сходимости, причем ряд, полученный после
интегрирования степенного ряда, имеет
тот же интервал сходимости, а его сумма
равна интегралу от суммы S(x)
исходного ряда. Таким образом, если
S(x)
=
,
то
;
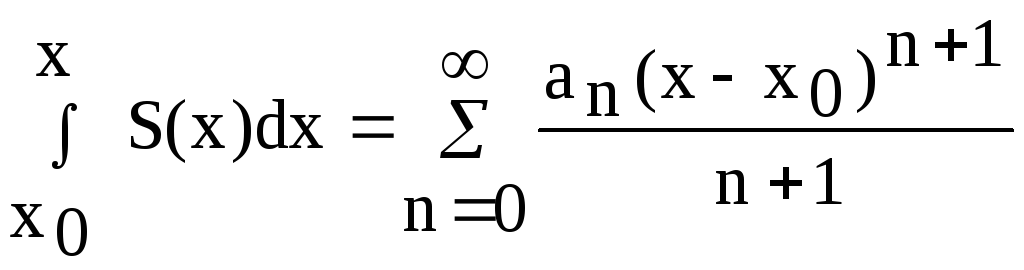-R
x
– x0
R
3. Ряд (5.10) можно почленно дифференцировать в каждой точке его области сходимости. При этом полученный ряд имеет тот же интервал сходимости, а его сумма равна производной от суммы S(x) первоначального ряда, т. е.
.
Замечание.Операции почленного дифференцирования и интегрирования можно производить сколько угодно раз.
Пример 3. Исследовать сходимость ряда
и найти его сумму.
Решение. Данный ряд составлен из членов бесконечной геометрической прогрессии со знаменателем q = x. Как известно, он сходится, когда | q | < 1, т. е. когда | х | < 1. Следовательно, областью сходимости данного ряда является интервал (1; 1).
Найдем сумму ряда по формуле
,
где а = 1, q
= x.
Тогда
.
Таким образом имеет место разложение
Пример 4. Найти сумму ряда
(
| x
| < 1).
Решение. Рассмотрим ряд
…
(6.11)
При
| х | < 1 его сумма
.
Исходный ряд может быть получен при
почленном дифференцировании данного
ряда.
Действительно,
(1 + х + х2 + х3 + … + хn + …)' = 1 + 2х + 3х2 + … + n xn1 +…
Тогда, согласно свойству 3 степенных рядов, сумма первоначального ряда равна производной от суммы ряда (5.11), т. е.
и, следовательно,
.
Пример 5.Найти сумму ряда
(
| х | < 1).
Решение. Дифференцируя почленно данный ряд, получим
1
+ х + х2
+ х3
+ … + хn
+ … =
.
Суммой
этого ряда при | х | < 1 является функция
(см. Пример 4).
.
Сумму первоначального ряда найдем, согласно свойству 2 степенных рядов, почленно проинтегрировав это выражение в пределах от 0 до х, т. е.
,
.
Найти область сходимости рядов
85.
; 86.
;
87.
;
88.
;
89.
;
90.
;
91.
;
92.
;
93.
;
94.
; 95.
;
96.
.
§5. Ряд Тейлора
Всякая функция, бесконечно дифференцируемая в некоторой окрестности точки х = х0 , может быть разложена в этой окрестности в сходящийся к данной функции степенной ряд.
(6.12)
если
выполняется условие
,
гдеrn(x)
– остаток ряда (6.12).
Коэффициенты ряда при этом представляются в виде
и называются коэффициентами Тейлора.
* n! = 1 2 3 … (n1) n («ЭН» факториал); 0! = 1; 1! =1.