Условный экстремум

Определение 2. Условным экстремумом функции z = f(x; y) называется экстремум этой функции, достигнутый при условии, что переменные x и y связаны уравнением (x; y) = 0 (уравнение связи).

Отыскание условного экстремума функции z = f(x; y) можно свести к исследованию на обычный экстремум функции Лагранжа u = f(x; y) + (x; y), где   неопределенный постоянный множитель.

Необходимые условия экстремума функции Лагранжа имеют вид

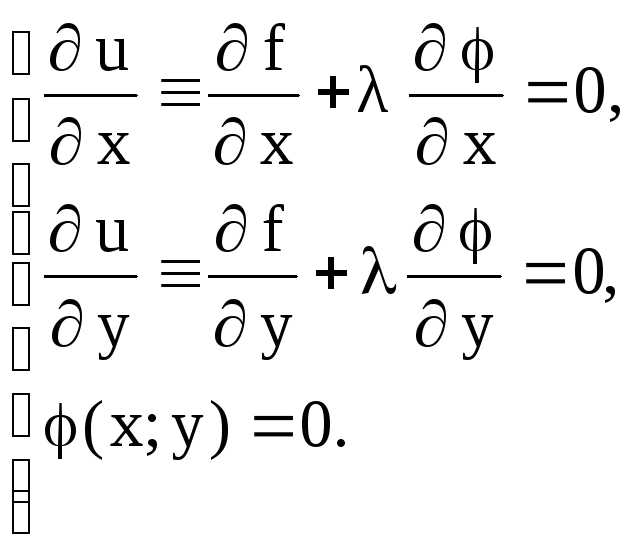
Из этой системы трех уравнений находят x и y  координаты точки, подозрительной на экстремум, и .

Пример 3. Найти экстремум функции z = xy при условии, что x и y связаны уравнением 2x + 3y  5 = 0.

Решение. Рассмотрим функцию Лагранжа u = xy + (2x + 3y  5). Имеем ,. Из системы уравнений, определяющей необходимые условия экстремума

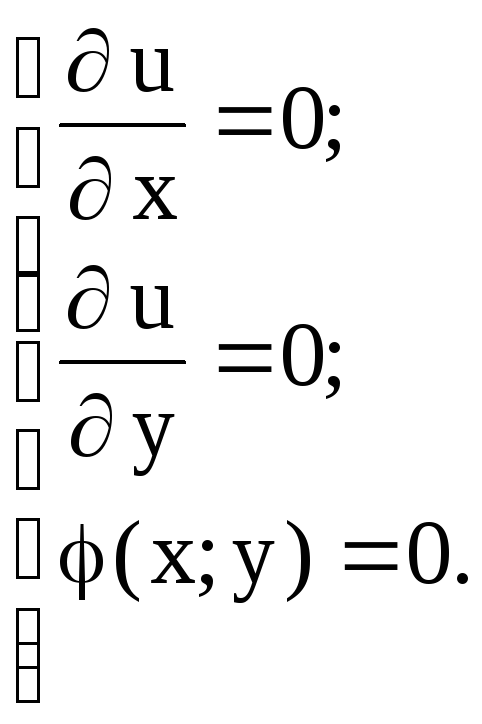
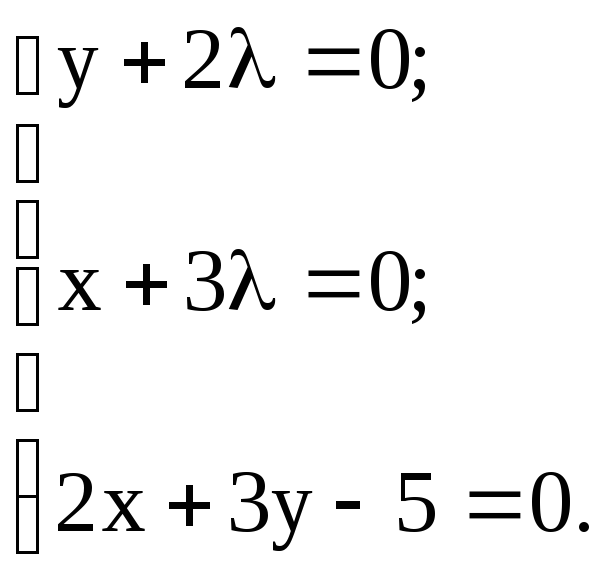
находим  = , x =, y =. Нетрудно проверить, что в точкефункция z = xy достигает наибольшего значения z_max = .

Пример 4. Из всех прямоугольных треугольников с заданной площадью S найти такой, гипотенуза которого имеет наименьшее значение.

Решение. Пусть x и y – катеты треугольника, а z – гипотенуза. Так как z² = x² + y², то задача сводится к нахождению наименьшего значения функции x² + y² при условии, что x и y связаны уравнением т. е. xy 2S = 0. Рассмотрим функцию Лагранжа u = x² + y² + (xy  2S) и найдем частные производные

; .

Так как x > 0, y > 0, то из системы уравнений

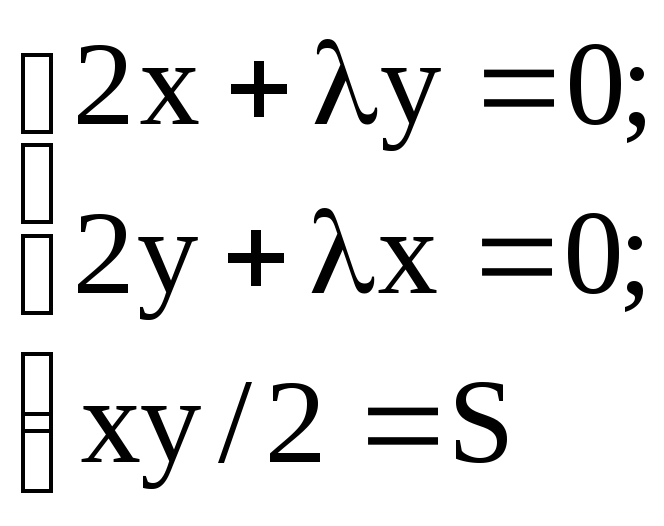
получаем решение  = 2, x = , y =.

Таким образом, гипотенуза имеет наименьшее значение, если катеты треугольника равны между собой.

Найти наибольшее и наименьшее значения функций:

332. z = x²  xy + y²  4x в замкнутой области, ограниченной прямыми x = 0, y = 0, 2x + 3y  12 = 0.

333. z = xy + x + y в квадрате, ограниченном прямыми x = 1, x = 2, y = 2, y = 3.

334. z = x² + 3y² + x  y в треугольнике, ограниченном прямыми x = 1, y = 1, x + y = 1.

335. z = sin x + sin y + sin (x + y) в области 0  x  , 0 y  .

336. z = xy в круге x² + y²  1.

337. z = 1  x²  y² в круге (x  1)² + (y  1)²  1.

338. z = x² + y² в круге (x  )² + (y  )²  9.

339. Найти экстремум функции z = x² + y², если x и y связаны уравнением = 1.

340. Из всех треугольников, имеющих периметр Р, найти наибольший по площади.

341. Из всех прямоугольников с заданной площадью S найти такой, периметр которого имеет наименьшее значение.

342. Определить размеры открытого бассейна объемом V, имеющего наименьшую поверхность.

343. Найти размеры прямоугольного параллелепипеда, имеющего при данной полной поверхности S максимальный объем.

344. Определить размеры цилиндра наибольшего объема при условии, что его полная поверхность S = 6.

* Под понятиями выпуклость и вогнутость графика функции следует понимать выпуклость вверх и вниз соответственно.

56