7. Общая схема исследования функций и построения графиков
Исследование заданной функции и построение ее графика целесообразно проводить в следующем порядке.
Найти область определения функции.
Исследовать функцию на четность и нечетность.
Исследовать функцию на периодичность.
Найти точки пересечения графика с осями координат.
Найти интервалы знакопостоянства функции.
Найти точки разрыва и асимптоты.
Найти критические точки первого рода.
Найти интервалы монотонности и точки экстремума.
Найти критические точки второго рода.
Найти интервалы выпуклости, вогнутости и координаты точек перегиба.
Построить график функции.
Пример
7. Исследовать
функцию f(x) =
и построить ее график.
Решение
1.
Функция определена на всей числовой
оси, кроме точек x = 
,
x =
,
в которых знаменатель обращается в
нуль, т.е.
D(f):
(;
)(
;
)(
;+).
Функция нечетная, т.к.
f(x)
=
.
Функция непериодическая.
Точки пересечения с осями координат находим из уравнения:
с
осью Оx: y = 0,
x=0;
с осью Оу: х = 0 у = 0.
Следовательно, график функции проходит через начало координат (0; 0).
Отметим на числовой оси точки, в которых функция не определена и точку пересечения с осью Ох и определим знак функции в каждом из полученных интервалов.
+
+
0
х
f(2)
=
f(1)
=
f(1)
=
f(2) =
Точками разрыва второго рода данной функции являются x =
и x =
.
Вычислим односторонние пределы в каждой
из них:
Отсюда
следует, что прямые x = 
и
x =
являются
вертикальными асимптотами графика
функцииf(x).
Горизонтальных
асимптот нет, т. к.
Найдем наклонную асимптоту у = kx + b, для чего вычислим
k
=
;
b
=
.
Итак, у = x уравнение наклонной асимптоты.
Вычислим
.
когда x2
(9
x2)
= 0, получим x = 0, x = 3
и x = 3
критические точки первого рода. В точках
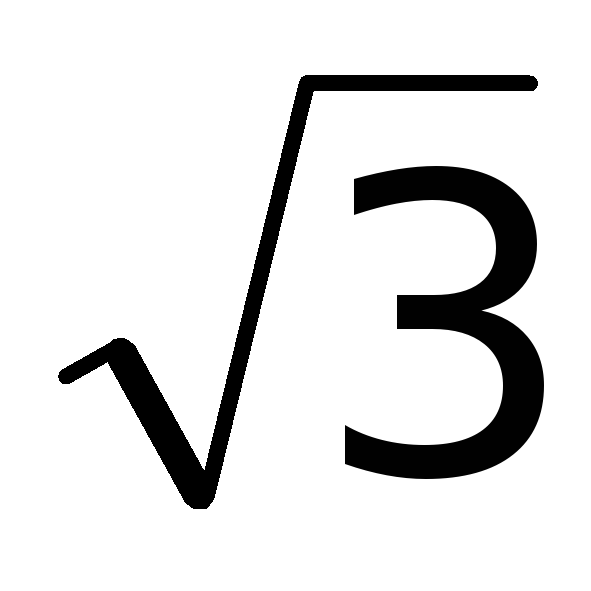x = 
,
x =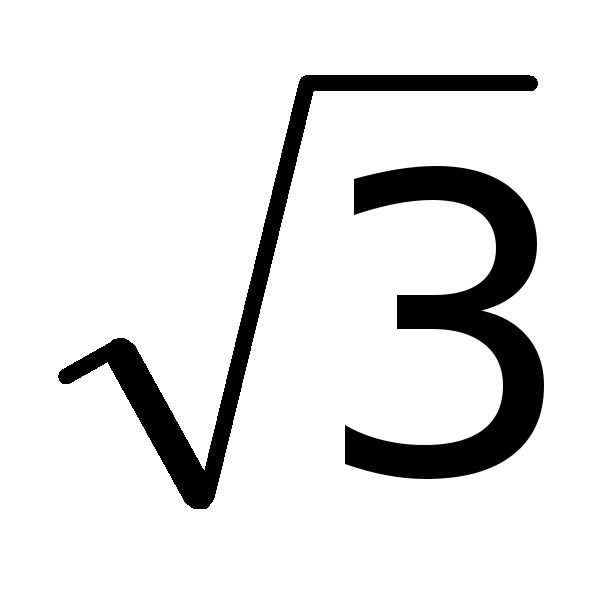
производная не существует и, следовательно,
они также являются критическими точками
первого рода данной функции.Расставим критические точки на числовой оси и определим знаки производной
в каждом из полученных интервалов. Так
как x2
0, (3
x2)2
0, то знак производной определяется
знаком разности 9
x2.
Поэтому при 
< x <3
и 3 < x < +
и, следовательно, функция убывает в
этих интервалах, а при3
< x < 
,
и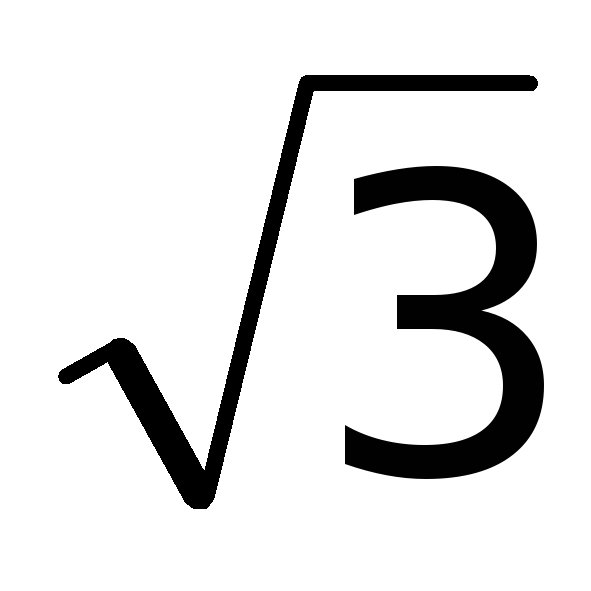
< x < 3
и
функция возрастает.
min max
+ +
+ +
3
0
3 х
В точке x = 3 производная меняет знак с () на (+), а в точке x = 3 c (+) на (). Поэтому согласно Теореме 4 точка x = 3 является точкой минимума, а x = 3 точкой максимума данной функции. Вычислим значения функции в точках максимума и минимума.
ymin
= f(3)
=
;
ymax
= f(3) =
.
Итак,
координаты минимума функции
и максимума
.
Вычислим
.
Очевидно,
только при х = 0, кроме того, вторая
производная не существует при x =
,
следовательно, эти точки являются
критическими точками второго рода.
10.
Расставим критические точки второго
рода на числовой оси и определим знак
в каждом из полученных интервалов.
+
+
0
х
;
;
;
Тогда,
согласно Теореме
6, на интервалах
(
и (0;
график функции вогнутый, а на интервалах
и (
выпуклый. Точка с координатами (0; f(0)=0),
в которой вторая производная равна
нулю, является точкой перегиба.
11.
Построим график функции. Для этого на
плоскости (x; y)
отметим точки разрыва x =
,
экстремумы: min
,
max
и точку перегиба графика функции (0;
0), построим асимптоты x =
,
=
,
y =x.
Используя данные пунктов 6 и 7, отметим предельные значения функции вблизи точек разрыва и при x . Соединив отмеченные точки плавной кривой, получим график функции.
у
3
3 0 
х
Построить графики функций
260. f(x) = x3 3x 261. f(x) = 12x x3
262.
f(x) =
263. f(x) =
264.
f(x) = x
265. f(x) = x (x
1)2/3
266.
f(x) =
267. f(x) =
268.
f(x) =
269. f(x) =
270.
f(x) =
271. f(x) =
272.
f(x) =
273. f(x) =
274.
f(x) =
275. f(x) = ln
276.
f(x) = x ex/2
277. f(x) =
278. f(x) = x2 e1/x 279. f(x) = x3 ex
280.
f(x) = x
281. f(x) = x3
ex
282.
f(x) =
283. f(x) =