Понятие о двойственных задачах линейного программирования

Пусть дана задача линейного программирования в стандартной форме: (1).

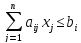, i=1,..m (2)

,j=1,..n(3)

Для перехода к двойственной задаче вводятся новые переменные yi, i=1,..m. При этом любая переменная yi соответствует одному из неравенств (2). После этого записывается двойственная задача в следующем виде:

(4)

, j=1,..n (5)

,i=1,..m(6)

Задача (4),(5),(6) называется двойственнойпо отношению к (1),(2),(3). При этом справедливо и обратное, т.е. если задачу (4),(5),(6) рассматривать как прямую задачу линейного программирования, то (1),(2),(3) будет двойственной по отношению к (4),(5),(6).

Правила состояния двойственной задачи для стандартной прямой задачи

1. Любому ограничению вида (2) прямой задачи сопоставляется двойственная переменная yi, i=1,..m;

2. Правые части ограничений прямой задачи, т.е. biстановятся коэффициентами целевой функцииz’ двойственной задачи, и критерий оптимальности меняется на простой: min max, maxmin;

3. Любой переменной xjпрямой задачи соответствуют ограничения двойственной задачи. При этом матрица коэффициентов A = [aij]mxnпрямой задачи транспонируетсяA’nxm=A^T;

4. Правые части ограничений двойственной задачи являются коэффициентами целевой функции прямой задачи. При этом смысл неравенства меняется на противоположный.

Пример

Прямая: Z = 3x1+2x2

Составим двойственную задачу:

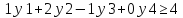
Экономический смысл двойственной задачи: Переменные yi двойственной задачи (4),(5),(6) рассматриваются как оценка стоимости одной единицы i-того ресурса, тогдаZ’ в выражении (4) дает оценку затрат на все ресурсы в количествахbiи целевая функция (4) должна быть минимальна.

Первая теорема двойственности: Если одна из задач (1),(2),(3) и (4),(5),(6) имеют решения оптимальный план и при этом значения целевой функции на этих оптимальных планах совпадаютZ(X*) =Z(Y*), при этом векторY* будет с теневыми ценами соответствующих ресурсов прямой задачи. Если же целевая функция одной из этих задач не ограничена, то другая задача вообще не имеет дополнительных планов.

Вторая теорема двойственности: Если задачи (1),(2),(3) и (4),(5),(6) имеют оптимальные решенияX* и Y*, то эти решения удовлетворяют соответствующим условиям:

(7), i=1,..m

(8),j=1,..n

Из условия (7) вытекает два следствия:

1. =>

2. =>

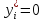
Эти условия означают, если i-тый ресурс в задаче (2) является недефицитным, то в оптимальном решении ему соответствует теневая цена = 0. Второе условие означает, что если i-тый ресурс имеет ненулевую теневую цену, то в оптимальном плане производства этот ресурс используется полностью, т.е. является дефицитным.

Из (8) следует:

1. =>

2. =>

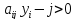Эти условия означают, что

1. если сумма ..., то оптимальный план производства не выполняет выпуск или производство этого вида продукции;

2. если в оптимальном плане планируется ненулевой V j-того продукта, то теневые цены ресурсов, затраченных на производство одной единицы этого продукта равны с ценой этого продукта.

Поиск оптимального решения при игре с природой

В теоретико-игровых моделях природойназывается объект В обладающий следующими свойствами:

1. Природа не ставит сознательной цели препятствовать выигрышу игрока А, поэтому вместо термина «стратегия игрока В» обычно используется термин «состояние природы»;

2. Состояние природы в общем случае неизвестно.

Игрок А должен принять решение о выборе своей стратегии в условиях, когда состояние природы неизвестно. Решение должно проверяться в условиях неопределенности.

	B1	B2	B3
A1	5	4	1	(5+4+1)/3 = 10/3
A2	4	4	2	(4+4+2)/3 = 10/3
A3	3	4	2	(3+4+2)/3 = 9/3
A4	2	1	5	(2+1+5)/3 = 8/3

aij– выигрыш игрока, если он выберет стратегию βi. При выборе стратегии в условиях неопределенности невозможно однозначно указать оптимальную стратегию. Эта стратегия будет зависеть от двух основных факторов:

1. Степени информативности игрока А относительно возможных состояний природы;

2. Склонности игрока А к риску.

С учетом этих факторов различают следующие критерии выбора оптимальных стратегий игроком А:

1. Критерий учитывает прогноз состояния природы. Если возможно дать достаточно надежный прогноз возможного состояния природы (например, В = В2), то оптимальную стратегию следует выбирать путем анализа столбца В2 с учетом возможного доминирования строк. Если доминирующей стратегии нет, то возможен выбор минимальных стратегий с учетом данного прогноза, то … прогнозируется с учетом ожидаемого риска;

2. Критерий Лапласа: Если можно принять гипотезу о равновероятности всех состояний природы, то наиболее разумно выбрать стратегию по условию максимального мат.ожидания выигрыша;

3. Критерий Вальда(пессимистический критерий, максиминный критерий, нижняя цена игры): α – гарантированный выигрыш игрока А при самом неблагоприятном состоянии природы;

4. Критерий Сэвиджа(критерий минимизации максимального риска)

Риск – принятие решения Ai игроком. А – величина rij=maxaij–aij=bj–aij.

Матрица рисков R

	B1	B2	B3	max rij
A1	0	0	4	4
A2	1	0	3	3
A3	2	0	2	2
A4	3	3	0	3
βj	5	4	5

rij– упущенный выигрыш игрока А при выборе им стратегии Аi от незнания состояния природы.

Критерий Сэвиджа рекомендует выбирать ту стратегию Аi, который соответствует минимум максимального риска. В данном примере и по критерию Вальда, и по критерию Сэвиджа рекомендуется одна и та же оптимальная стратегия А3. В общем случае, эти критерии могут давать разные рекомендации. Однако при принятии ответственных решений целесообразно анализировать выбор с точки зрения разных критериев, и, если рекомендации по нескольким критериям совпадают, то это повышает уверенность в правильности выбора, т.е. увеличивает надежность. Критерий Сэвиджа также как и критерий Вальда является пессимистическим, только здесь другая оценка пессимизма.

5. Критерий крайнего оптимизма

5 A1

4

4

5 A4

6. Критерий Гурвица

Вводится числовой показатель 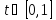, который называется степенью оптимизма и рекомендуется выбор стратегии Ai. По условию,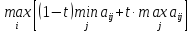

t= 0 – критерий крайнего оптимизма, t = 1 – критерий Вальда.

12