МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Государственное образовательное учреждение высшего профессионального образования

«Новгородский государственный университет имени Ярослава Мудрого»

_________________________________________________________________

Институт сельского хозяйства и природных ресурсов

Контрольная работа по дисциплине

« Гидравлика»

Выполнил студент

1 курса, гр.1511 зу

Кремнев О.И.

Проверил:

Сансиев В.Г.

Великий Новгород

2012

шифр - 09 последние две цифры 09 (вариант - 9, условие - 0).

Согласно методическим указаниям и контрольным заданиям для

студентов- заочников инженерно-технических специальностей

вузов. В. П. Норкус, В. А. Стапонкус, И. А. Малинаускас; Под ред. Ю. Ю. Мацевичюса.— 5-е изд., перераб. и доп.— М.: Высш. шк., 1989.— 56 с: ил.

Задача 3

(рис.7). Зазор между валом и втулкой заполнен маслом, толщина слоя которого равна . Диаметр вала D, длина втулки L. Вал вращается равномерно под воздействием вращающего момента М. Определить частоту вращения вала, если температура масла равна 40^оС.

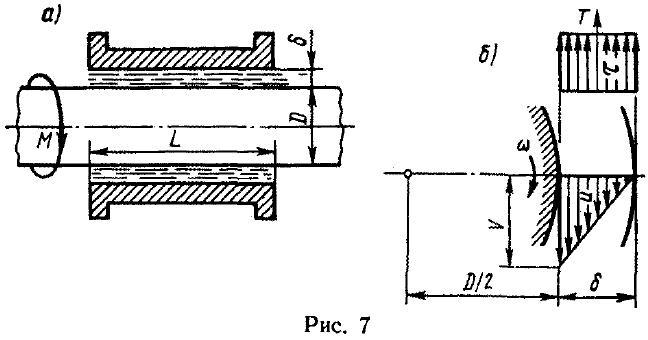Д ано:

Масло: Индустриальное 30,

,

М = 8,50 Нм,

δ = 1,9 мм,

D = 200 мм,

L = 630 мм.

Определить: n — частоту вращения вала.

Решение

Эта задача составлены по теме «Основные свойства жидкостей». В этой задаче рассматривается вязкость жидкости.

Задачу решим с помощью формулы Ньютона:

где Т – сила трения; – динамическая вязкость масла; А – площадь соприкосновения твердой поверхности с жидкостью; du/dn – градиент скорости.

Площадь соприкосновения вала с жидкостью определим по формуле:

Динамическая вязкость жидкости определяем по формуле:

где – кинематическая вязкость масла; – плотность масла.

Кинематическая вязкость масла индустриального 30, при температуре 40^оС, определяем по приложению 1: .

Плотность масла индустриального 30, при температуре 40^оС, определяем по формуле:

где – плотность масла при температуре ; – изменение температуры; Т_о – температура, при которой плотность жидкости равна , – коэффициент температурного расширения жидкости (в среднем для минеральных масел можно принять .

По приложению 1 определяем плотность масла индустриального 30, при температуре 50^оС: .

Тогда

По формуле (4) определяем плотность масла индустриального 30 , при температуре 40^оС:

Поскольку толщина слоя масла мала, можно считать, что скорости в нем изменяются по прямолинейному закону. Следовательно, градиент скорости .

Тогда формула преобретает вид:

Силу трения определяем из формулы момента:

Из-за малости зазора вторым членом в скобках можно пренебречь.

При малом зазоре, когда , кривизной слоя жидкости пренебрегаем, рассматривая ее движение в зазоре как плоскопараллельное (см. рис.7, б). Считая, что скорости u в слое масла изменяются по прямолинейному закону, эпюра касательных напряжений имеет вид прямоугольника. Следовательно, сила трения Т проходит через центр тяжести этой эпюры, т. е. по середине слоя масла.

Частоту n вращения вала и угловую скорость определяем при помощи известных формул:

, , (8)

Подставляя в формулу выражения и выведем формулу для определения частоты n вращения вала:

Ответ: — частота вращения вала.

Задача 5

(рис.9). Вертикальная цилиндрическая цистерна с полусферической крышкой до самого верха заполнена жидкостью, плотность которой . Диаметр цистерны D, высота ее цилиндрической части Н. Манометр М показывает манометрическое давление . Определить силу, растягивающую болты А, и горизонтальную силу, разрывающую цистерну по сечению 1–1. Силой тяжести крышки пренебречь. Векторы сил показать на схеме.

Д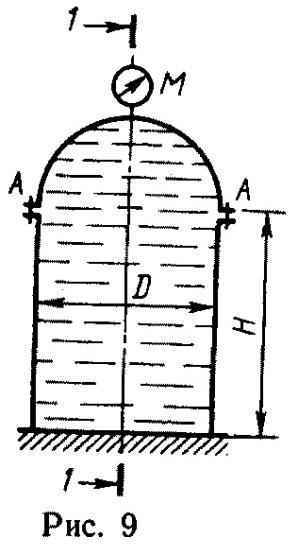 ано:

D = 1,9 м,

H = 3,8 м,

,

.

Определить: Fz и Fx — силу, растягивающую болты А, и горизонтальную силу, разрывающую цистерну по сечению 1–1.

Решение

Эта задача составлены по теме «Гидростатика». Она связана с определением силы давления жидкости на криволинейные стенки.

Изобразим на схеме цистерны силу Fz, растягивающую болты А, и горизонтальную силу Fx, разрывающую цистерну по сечению 1–1

Р исунок — 1

1. Вертикальная сила F_z, растягивающую болты А, равна весу жидкости, занимающей объем V тела давления. Определяем вертикальную силу F_z, растягивающую болты А, по формуле:

Телом давления называется тело, с одного конца ограниченное криволинейной поверхностью, с другого – пьезометрической плоскостью, а со сторон – вертикальной проектирующей поверхностью.

При построении тела давления крышка проектируется вертикально вверх на горизонтальную пьезометрическую плоскость. Вертикальное расстояние до этой плоскости определяют по формуле:

Отсюда, учитывая, что найдем F_z:

Определяем численное значение F_z:

2. Горизонтальная сила F_x равна силе давления на вертикальную проекцию криволинейной стенки и определяется так же, как и сила давления на плоскую поверхность по формуле:

,

где р_с – давление в центре тяжести вертикальной проекции плоской фигуры; А – площадь проекции криволинейной стенки на вертикальную плоскость.

Полную горизонтальную силу F_х, разрывающую цистерну по сечению 1—1, удобно разложить на две части: силу F₁, действующую на верхнюю, полусферическую часть цистерны, и силу F₂, которая действует на ее цилиндрическую часть. Силы F₁ и F₂ вычисляем по формуле .

Определим F₁ по формуле :

Площадь проекции полусферической крышки на вертикальную плоскость сечения 1-1, определим как площадь полукруга:

Положение центра тяжести полукруга находится на расстоянии от манометра:

Давление в центре тяжести вертикальной проекции плоской фигуры определим по формуле

Отсюда, вычисляем F₁ по формуле (5):

Определим F₂ по формуле :

Площадь проекции цилиндрической части цистерны на вертикальную плоскость сечения 1-1, определим как площадь прямоугольник:

Положение центра тяжести прямоуольника находится на расстоянии y от диаметра:

Давление в центре тяжести вертикальной проекции плоской фигуры определим по формуле

Отсюда, вычисляем F₂ по формуле :

Полную горизонтальную силу F_х, разрывающую цистерну по сечению 1—1, опеределим как сумму сил действующих на части цистерны:

Ответ: - сила, растягивающая болты А; - горизонтальная сила, разрывающая цистерну по сечению 1–1.

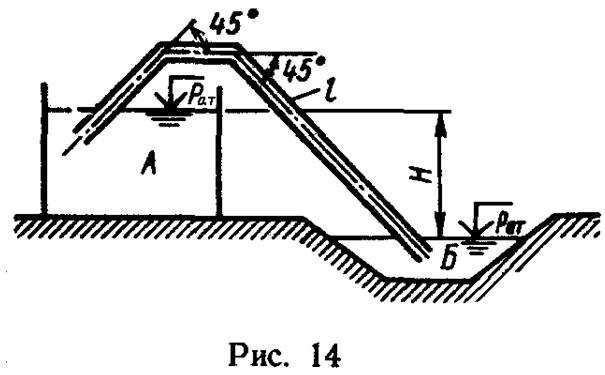
Задача 10

(рис.14). По сифонному трубопроводу длиной l жидкость Ж при температуре 20°С сбрасывается из отстойника А в отводящий канал Б. Какой должен быть диаметр d трубопровода (его эквивалентная шероховатость _э), чтобы обеспечить сбрасывание жидкости в количестве Q при напоре H? Трубопровод снабжен приемным клапаном с сеткой (), а плавные повороты имеют углы 45° и радиус округления R=2r. Построить пьезометрическую и напорную линии. Данные в соответствии с вариантом задания выбрать из табл.4.

Дано:

Ж — Дизельное топливо

T = 20°С,

Q = 2,7 л/с,

H = 4,5 м,

l = 14,7 м,

,

.

Определить: d — диаметр трубопровода. Построить пьезометрическую и напорную линии.

Решение

Будем решать задачу с помощью уравнения Бернулли, которое составляется для двух живых сечений потока и для установившегося движения реальной жидкости имеет следующий вид:

где z – геометрический напор или высота положения – расстояние от произвольно выбранной горизонтальной плоскости сравнения до центра тяжести сечения; p – давление в центре тяжести сечения; – пьезометрический напор – вертикальное расстояние между центром тяжести сечения и уровнем жидкости в пьезометре (удельная потенциальная энергия давления); – средняя скорость потока в сечении; - коэффициент Кориолиса (отношение действительной кинетической энергии потока к условной кинематической энергии, вычисленной по средней скорости); – скоростной напор (удельная кинетическая энергия); – гидравлические потери напора (та часть удельной механической энергии, которую жидкость теряет на преодоление сопротивлений на участке потока между сечениями 1 и 2).

Выберем z₁ и z₂ таким образом, чтобы

Уравнение постоянства расхода:

где – средняя скорость движения жидкости, S - площадь живого сечения потока.

Уравнение неразрывности потока:

Так как по условию задачи трубопровод имеет одинаковый диаметр по всей длине (), то и средние скорости движения жидкости будут одинаковыми на всех участках трубопровода .

Потери напора в трубопроводе слагаются из потерь на трение по длине и потерь на преодоление местных сопротивлений:

Потери напора по длине трубопроводов:

где - коэффициент сопротивления трения по длине l; d – внутренний диаметр трубы; – средняя скорость движения жидкости.

Потери напора на преодоление местных сопротивлений в нашем случае:

т.к. у нас всего четыре участка, где могут происходить потери напора на преодоление местных сопротивлений: вход в трубу, два поворота и выход из трубы. Здесь , , – это коэффициенты местных сопротивлений. Коэффициент сопротивления приемного клапана с сеткой известен из условия задачи - , коэффициент при выходе из трубы равен 1 - , по приложению 4, а т.к. по условию задачи радиус поворота в

обоих случаях равен диаметру трубы, то коэффициенты сопротивления в плавных поворотах также можно принять равными 1 - .

Учитывая вышесказанное получим:

Тогда потери напора в трубопроводе:

Из основного уравнения гидростатики получим

где – плотность дизельного топлива при T = 20°С определяем по приложению 1: .

Учитывая, что , а значения скоростного напора пренебрежимо малы по сравнению с другими членами уравнения и их можно приравнять к нулю , подставим в уравнение Бернулли уравнения и получим:

Откуда

Учитывая, что , получим:

Определим режим течения жидкости. Для этого определим диаметр d при :

где - кинематическая вязкость дизельного топлива при T = 20°С определяем по приложению 1: .

При ламинарном течении коэффициента гидравлического трения определяется по формуле .

Теперь воспользовавшись формулой , сравним получаемый напор с заданным

Режим течения, определяемый расходом Q = 2,7 л/с, будет турбулентным.

Число Рейльнодса для турбулентного движения определяем по формуле: .

Коэффициента гидравлического трения для любой области сопротивления при турбулентном режиме движения жидкости определим по формуле А.Д. Альтшуля:

Напора H определяем по формуле и составим таблицу 1 значений напора в зависимости от диаметром d трубопровода.

Таблица 1

d, мм	Re		H, м
40	3069	0,043	9,9
41	2995	0,043	8,9
42	2923	0,044	8
43	2855	0,044	7,2
44	2790	0,044	6,5
45	2728	0,044	5,9
46	2669	0,045	5,3
47	2612	0,045	4,8
48	2558	0,045	4,4
49	2506	0,045	4
50	2456	0,045	3,7

Построим график взаимозависимости между высотой напора H и диаметром d трубопровода (см. рисунок 1), используя данные из таблицы 1.