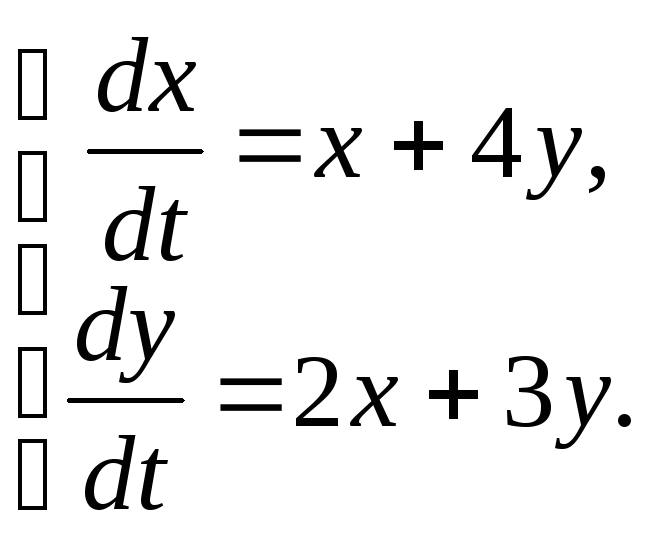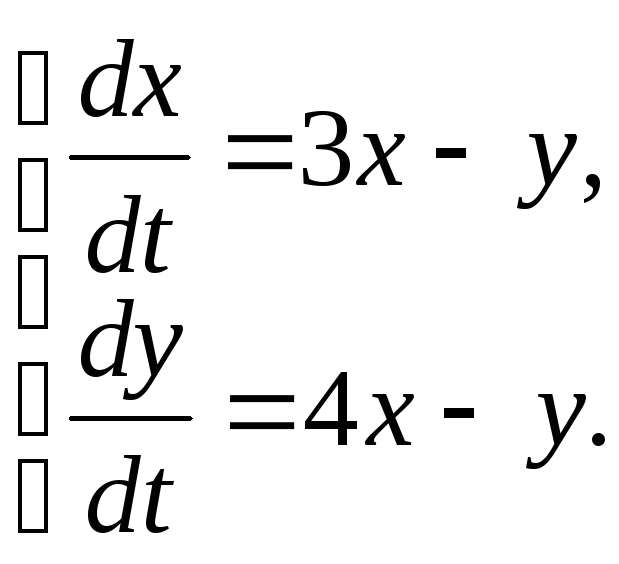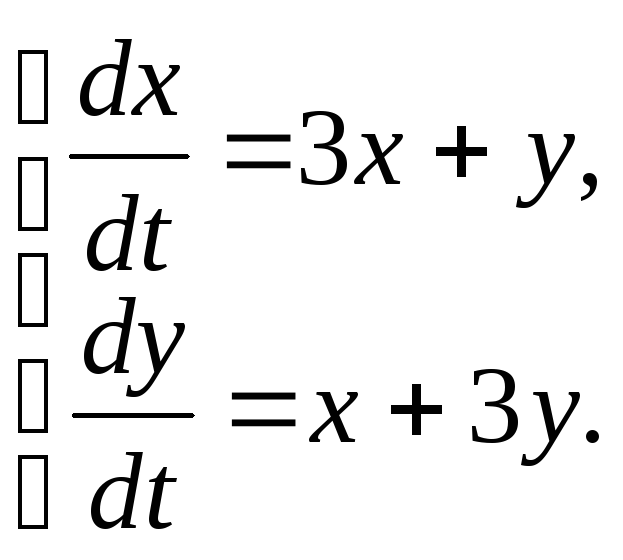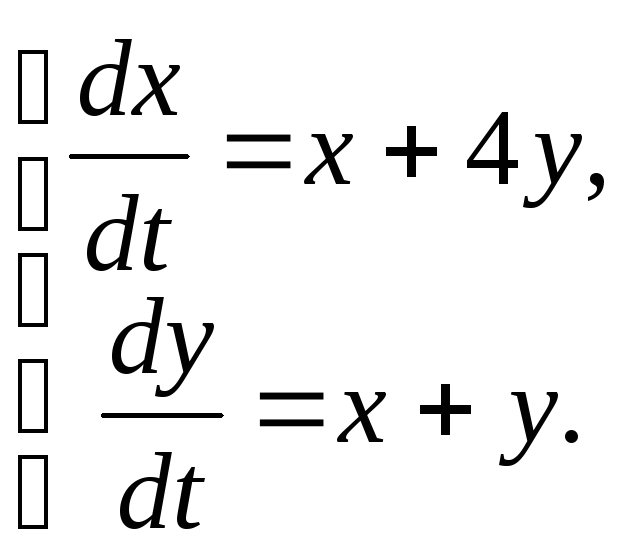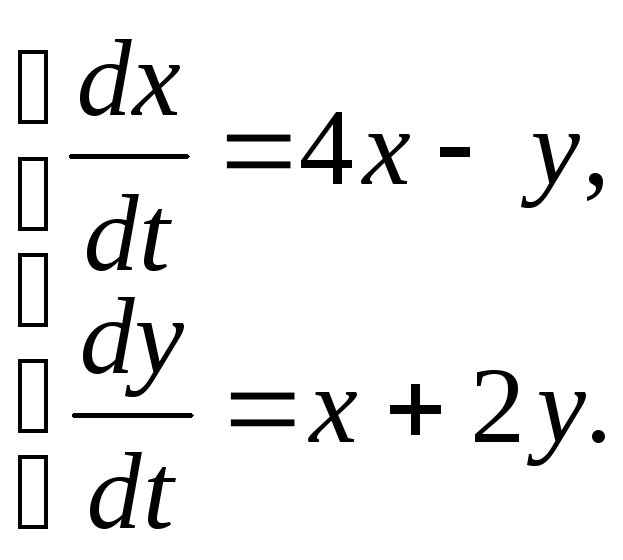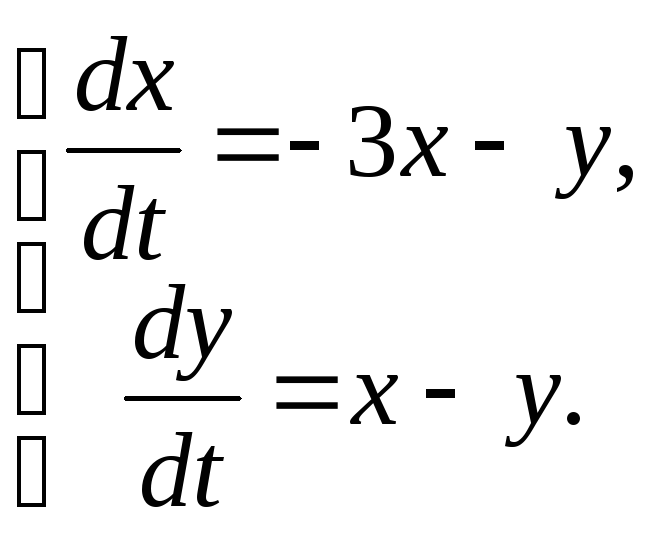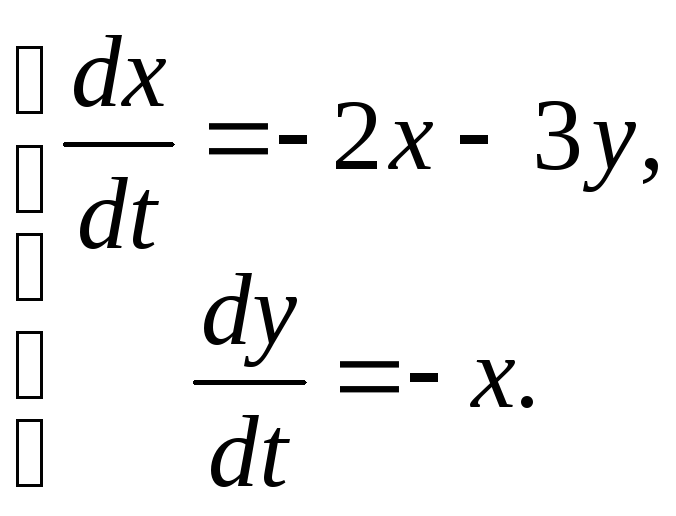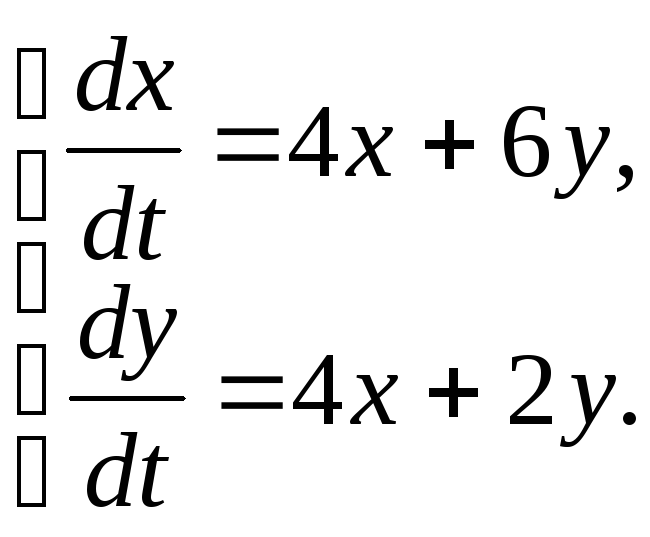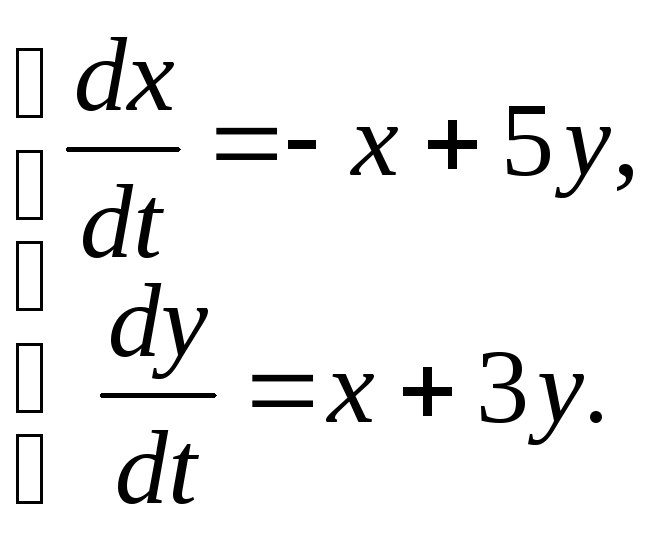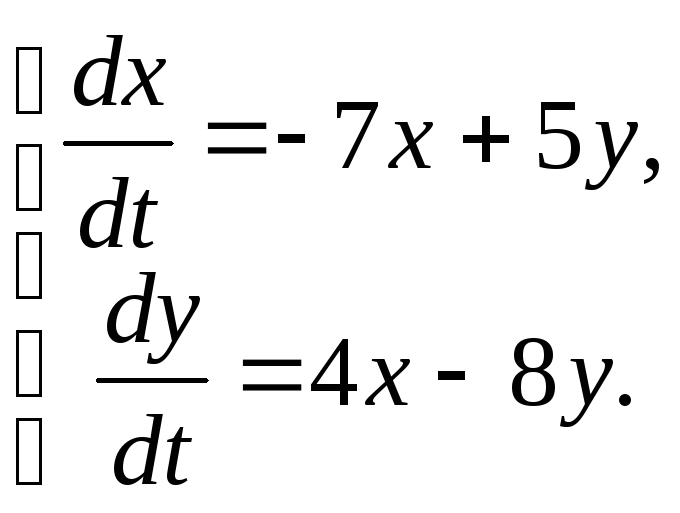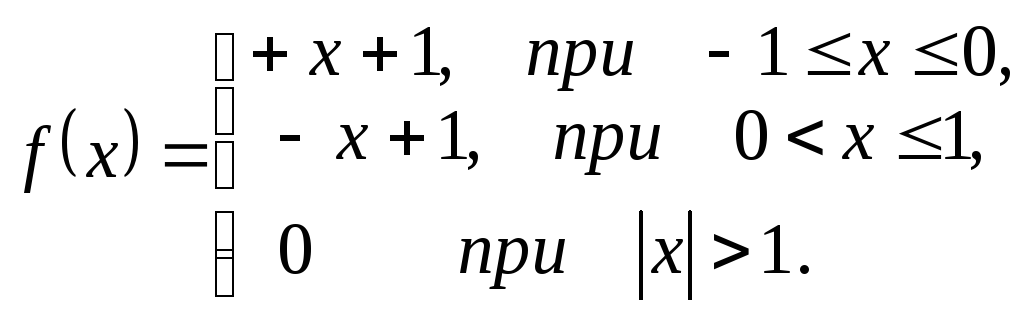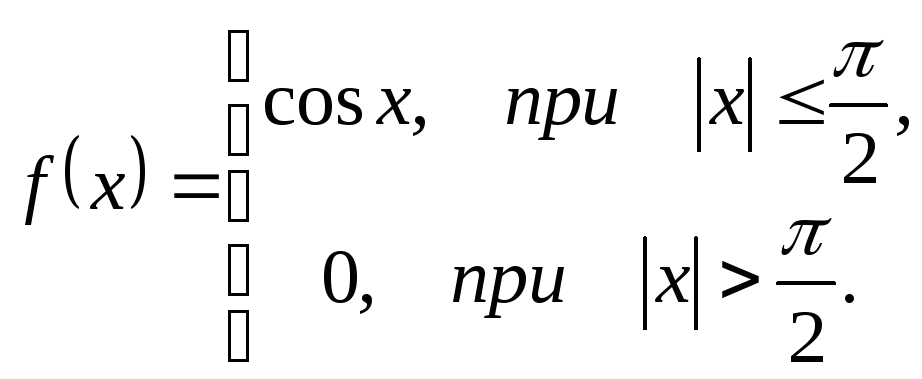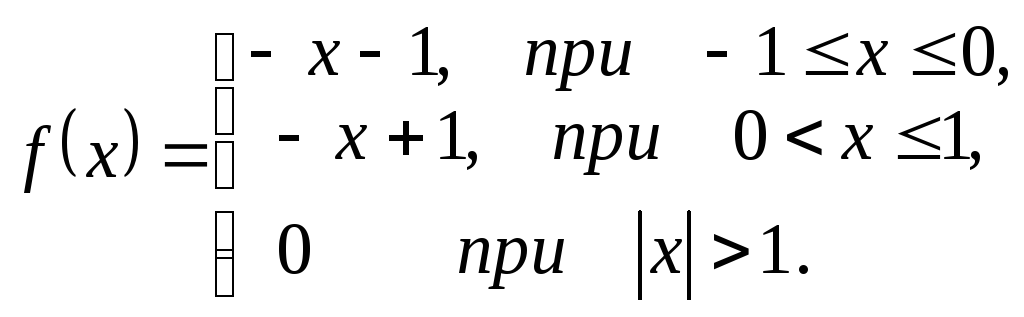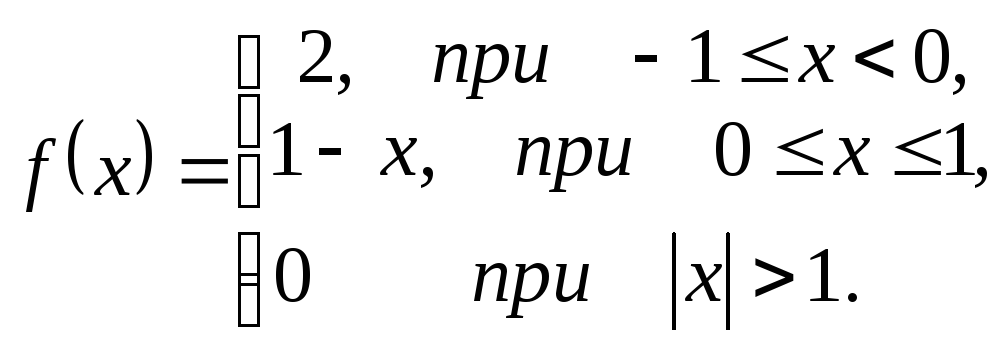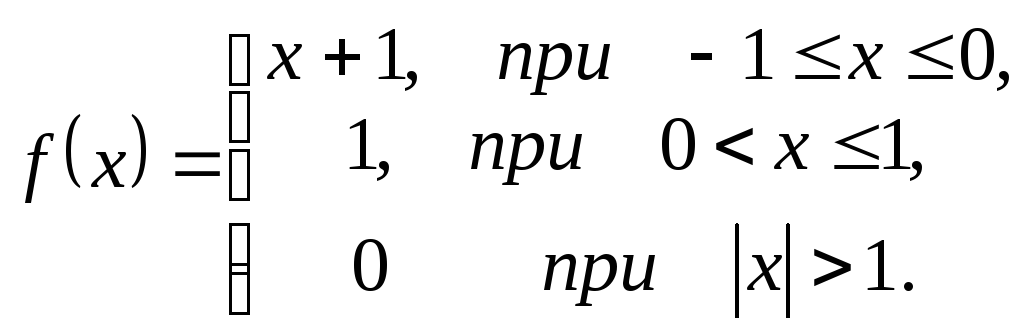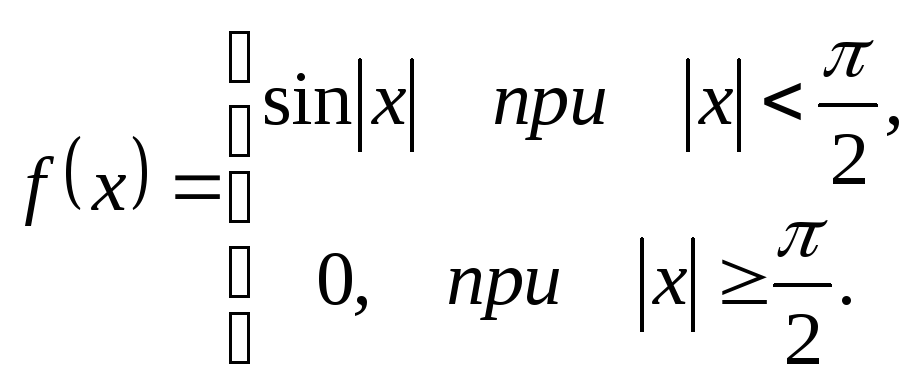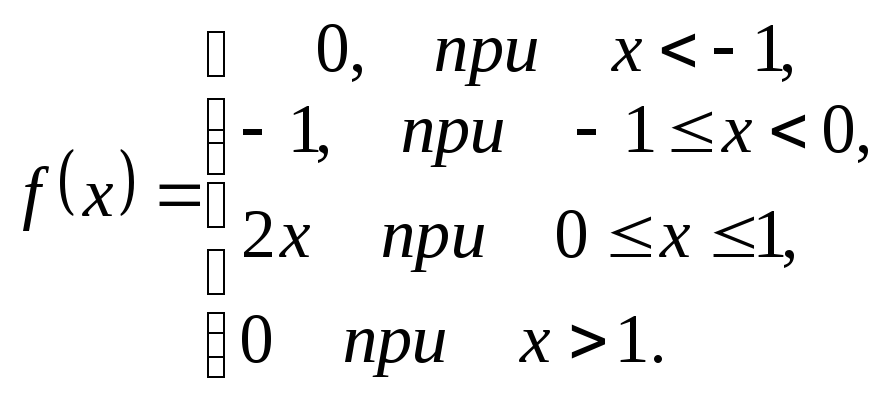Задачи для контрольных работ Контрольная работа №3

Комплексные числа. Неопределенные и определенные интегралы

1-10.Дано комплексное число . Требуется: а) записать числов алгебраической и тригонометрической формах; б) вычислить; найти все корни уравнения.

5. 9.

6. 10.

7.

4. 8.

11-20. Найти неопределенные интегралы. В пунктах а) и б) результаты проверить дифференцированием.

11. а)	б)	в)	г)
12. а)	б)	в)	г)
13. а)	б)	в)	г)
14. а)	б)	в)	г)
15. а)	б)	в)	г)
16. а)	б)	в)	г)
17. а)	б)	в)	г)
18. а)	б)	в)	г)
19. а)	б)	в)	г)
20. а)	б)	в)	в)

21-30. Вычислить определенные интегралы

21. ;	22.;	23.;	24.;
25.;	26.;	27. ;	28.;
29. ;	30. .

31-40. Вычислить несобственные интегралы (или установить их расходимость)

31. ;	32. ;	33. ;	34. ;
35. ;	36. ;	37. ;	38. ;
39. ;	40. .

41-50. Вычислить интеграл с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

41. ;	42. ;
43. ;	44. ;
45. ;	46. ;
47. ;	48. ;
49. ;	50. ;

51. Найти площадь фигуры, ограниченной кривыми и осью.

52. Найти площадь фигуры, ограниченной кривой и прямыми.

53. Найти площадь фигуры, ограниченной кривыми и.

54. Найти площадь фигуры, ограниченной кривыми и.

55. Найти площадь фигуры, ограниченной одной аркой циклоиды и осью.

56. Найти площадь фигуры, ограниченной кривой .

57. Найти длину одной арки циклоиды.

58. Найти длину полукубической параболы от начала координат до точкиВ(4,8).

59. Найти объем тела, образованного вращением вокруг оси фигуры, ограниченной кривымии.

60. Найти площадь поверхности, образованной вращением вокруг оси дуги параболымежду точками пересечения с прямой.

Контрольная работа №4 Дифференциальные уравнения. Ряды

61-70. Найти общее решение дифференциального уравнения

61. а) ;	б) ;
62. а) ;	б) ;
63. а) ;	б) ;
64. а) ;	б) ;
65. а) ;	б) ;
66. а) ;	б) ;
67. а) ;	б) ;
68. а) ;	б) ;
69. а) ;	б) ;
70. а) ;	б) .

71-80.Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям:

71.
72.
73.
74.
75.
76.
77.
78.
79.
80.

81-90. Найти общее решение системы линейных дифференциальных уравнений

81.	82.
83.	84.
85.	86.
87.	88.
89.	90.

91-100. Исследовать сходимость числового ряда

91.	92.	93.
94.	95.	96.
97.	98.	99.
100.

101-110. Найти интервал сходимости степенного ряда

101.	102.
103.	104.
105.	106.
107.	108.
109.	110.

111-120. Разложить данную функцию в ряд Фурье в указанном интервале

111. в интервале.

112. в интервале.

113. в интервале

114. в интервале.

115. в интервале.

116. в интервале.

117. в интервале.

118. в интервале.

119. в интервале

120. в интервале.

121-130. Для заданной функции найти преобразование Фурье

121.
122.
123.
124.
125.
126.
127.
128.
129.
130.
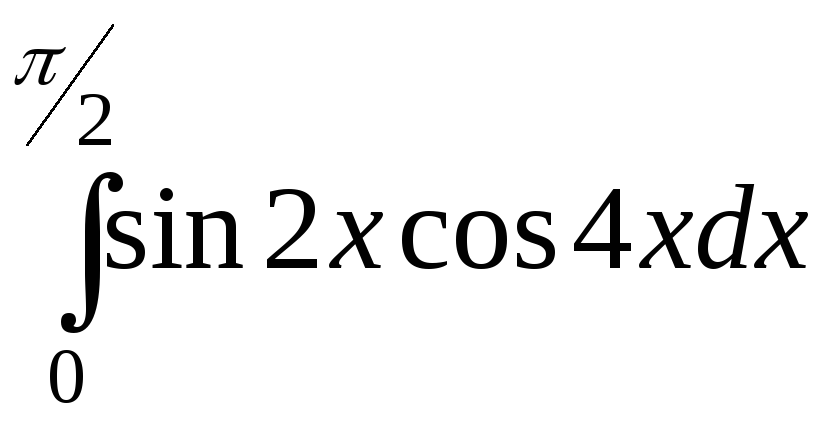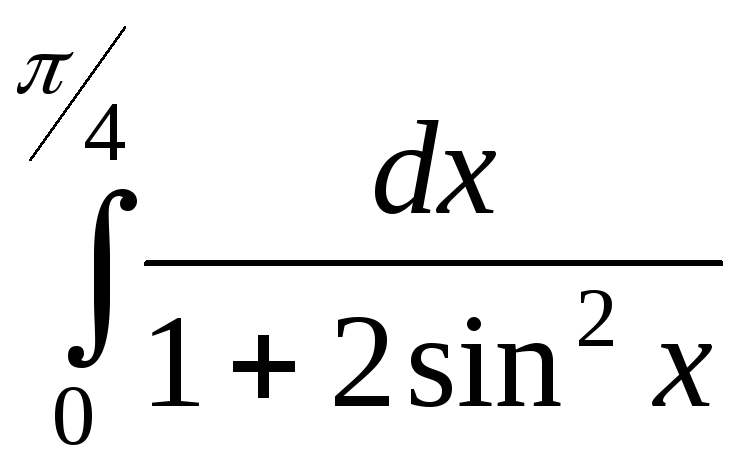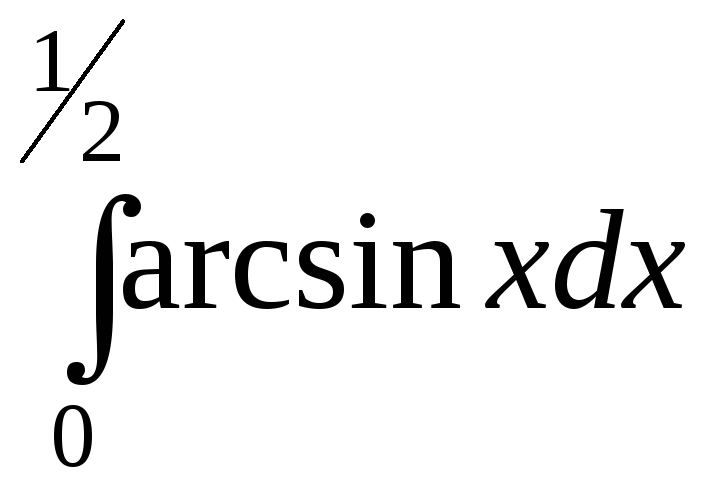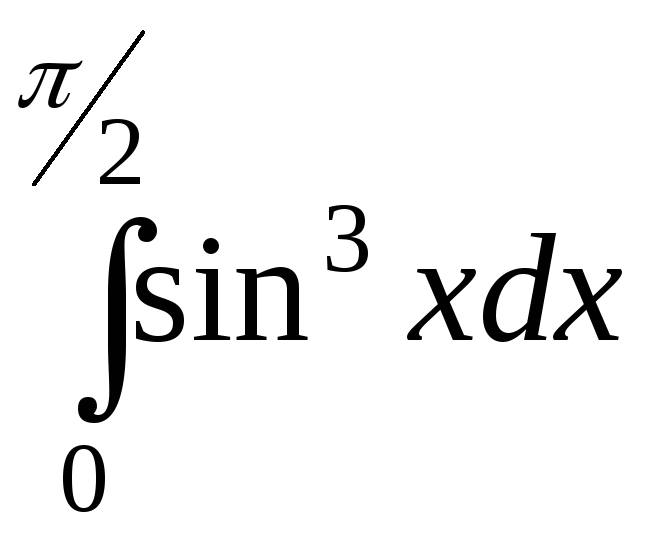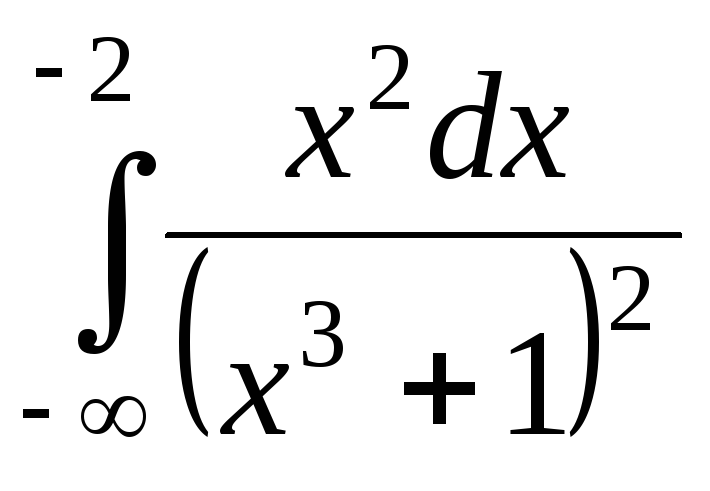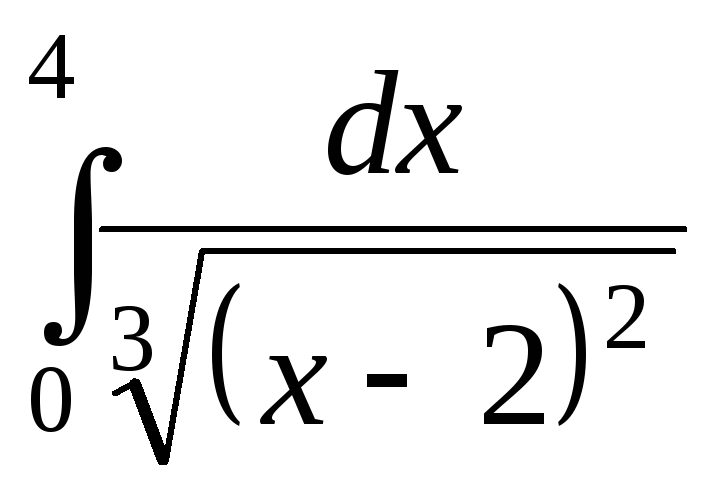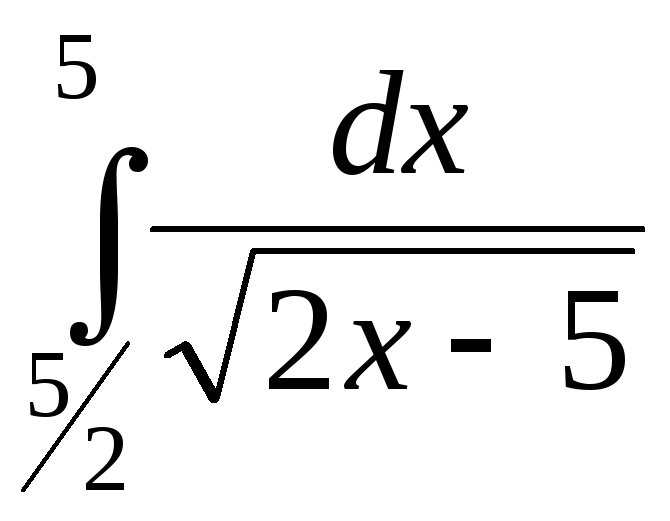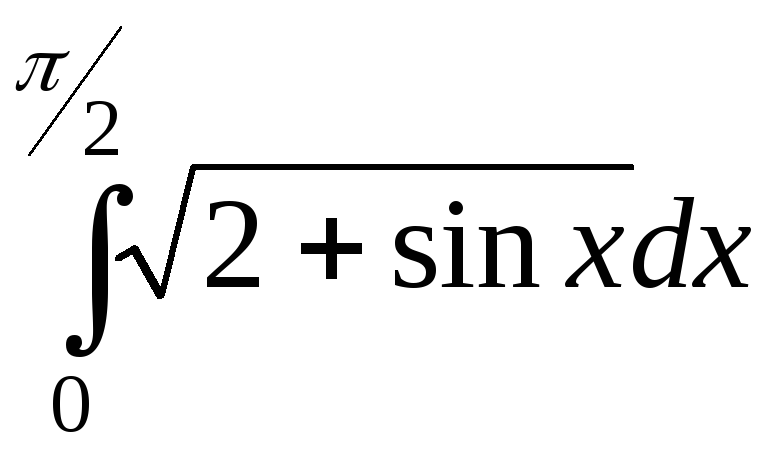