- •1. Действие сосредоточенной нагрузки на поверхности полупространства. Способ элементарного суммирования.
- •2. Распределение напряжений при равномерно распределенной нагрузке по площади прямоугольника. Метод угловых точек.
- •3. Распределение напряжений при действии равномерно распределенной нагрузки по полосе (по подошве ленточного фундамента).
- •4. Распределение напряжений от собственного веса грунта.
- •2 Расчет пластических осадок грунтовых оснований.
4. Распределение напряжений от собственного веса грунта.
Случай 1.
Основание представлено одним слоем
однородного грунта с постоянным весом
по глубине (![]() ),
грунтовые воды отсутствуют.
),
грунтовые воды отсутствуют.
|
|
|
Случай 2. Основание по глубине представлено несколькими слоями грунта, удельные веса каждого грунтового слоя неизменны, грунтовые воды отсутствуют.
|
|
|
Случай 3.
В грунтовом основании, представленном
однородным слоем, имеются грунтовые
воды, грунт взвешивается
![]() .
.
|
|
К расчету принимается двухслойное основание
1
|
Случай 4.
Слоистое грунтовое основание ниже
грунтовых вод представлено слоями
грунтов, испытывающих (![]() )
и не испытывающих (
)
и не испытывающих (![]() )
взвешивающее действие воды.
)
взвешивающее действие воды.
|
|
|
Пример 1.
Поверхность грунта
загружена на площади 2,5х4,0м равномерно
распределенной нагрузкой
![]() .
Определить величины сжимающих напряжений
(
.
Определить величины сжимающих напряжений
(![]() )
по осям, проходящим через: центр
загруженной площади (М1);
угол загруженной площади (М2),
точку внутри контура загружения на
расстоянии 0,25bи 0,25l
от центра (М3);
точку М4
за контуром
прямоугольника нагрузки на расстоянии
0,25lи0,25bот
угла. Построения эпюр выполнить до
глубины ≤10м.
)
по осям, проходящим через: центр
загруженной площади (М1);
угол загруженной площади (М2),
точку внутри контура загружения на
расстоянии 0,25bи 0,25l
от центра (М3);
точку М4
за контуром
прямоугольника нагрузки на расстоянии
0,25lи0,25bот
угла. Построения эпюр выполнить до
глубины ≤10м.
Решение для оси через М1:
|
|
Относительная
длина
Толща грунта
разбивается на условные слои
Расчеты приведены в табличной форме:
|
Решение для оси через М2:
|
|
Относительная
длина
Толща грунта
разбивается на условные слои
Расчеты приведены в табличной форме:
|
Решение для оси М3:
|
|
Точка М3 является угловой для 4-х прямоугольников загрузки
Мощность условного
слоя
| |||||||||
|
|
|
|
|
|
|
|
|
|
| |
|
0 1,0 2,0 3,0 4,0 5,0 6,0 7,0 |
0 1,6 3,2 4,8 6,4 8,0 9,6 11,2 |
1,00 0,588 0,232 0,118 0,070 0,046 0,032 0,024 |
0 1,0 2,0 3,0 4,0 5,0 6,0 7,0 |
1,00 0,795 0,469 0,284 0,181 0,125 0,090 0,068 |
0 0,533 1,067 1,600 2,133 2,667 3,200 3,733 |
1,00 0,899 0,756 0,558 0,412 0,308 0,232 0,182 |
0 1,6 3,2 4,8 6,4 8,0 9,6 11,2 |
1,00 0,638 0,358 0,227 0,155 0,109 0,082 0,062 |
40,0 29,20 18,95 11,87 8,19 5,88 4,36 3,36 | |
Решение для оси М4:
|
|
Влияние на напряжение по оси М4 оказывают 4-е прямоугольника:
Мощность условного
слоя
Расчеты приведены в табличной форме: | |||||||||
|
|
|
|
|
- |
|
- |
|
|
| |
|
0 1,0 2,0 3,0 4,0 5,0 6,0 7,0 |
0 0,32 0,64 0,96 1,28 1,60 1,92 2,24 |
1,00 0,983 0,912 0,797 0,673 0,558 0,463 0,385 |
0 1,0 2,0 3,0 4,0 5,0 6,0 7,0 |
1,00 0,814 0,528 0,352 0,241 0,178 0,134 0,103 |
0 1,6 3,2 4,8 6,4 8,0 9,6 11,2 |
1,00 0,641 0,371 0,250 0,184 0,139 0,110 0,100 |
0 1,6 3,2 4,8 6,4 8,0 9,6 11,2 |
1,00 0,558 0,232 0,118 0,071 0,046 0,032 0,024 |
0 0,86 2,45 3,13 3,19 2,87 2,51 2,06 | |
Пример 2.
Поверхность грунта
загружена равномерно распределенной
нагрузкой
![]() по площади прямоугольника с размерами
сторон
по площади прямоугольника с размерами
сторон![]() .
Определить сжимающие напряжения по
осям, проходящим через: центр площади
загружения (М1);
на контуре площади нагружения по средине
длины (М2),
под углом площади загружения (М3);
за контуром прямоугольника нагрузки
по средине длины на расстоянии 1м от
центра (М4).
.
Определить сжимающие напряжения по
осям, проходящим через: центр площади
загружения (М1);
на контуре площади нагружения по средине
длины (М2),
под углом площади загружения (М3);
за контуром прямоугольника нагрузки
по средине длины на расстоянии 1м от
центра (М4).
Решение для оси через М1:
|
|
Точка М1 расположена в центре площади нагружения
Коэффициент
|
Решение для оси через М2:
|
|
Точка М2
удалена
от краев прямоугольника нагружения
на
|
Решение для оси через М3:
|
|
Точка М3 угловая. Расчет напряжений по оси М3 выполняется как для угловых точек прямоугольной нагрузки
|
Решение для оси через М4:
|
|
Точка М4 расположнена на оси y на удалении 1,0м от центра подошвы. Напряжение определяется по схеме влияния полосовой нагрузки
Изменение глубины
точек по оси М4
принимается с шагом
|
Пример 3.
Основание состоит
из 3-х слоев грунта с поверхности залегает
слой песка мелкого:
![]() мощность слоя 3,0м. Ниже залетает слой
суглинок:
мощность слоя 3,0м. Ниже залетает слой
суглинок:![]() мощность слоя 4,8м. Под слоем суглинка
залегает слой супеси
мощность слоя 4,8м. Под слоем суглинка
залегает слой супеси![]() .
Уровень грунтовых вод на глубине 1,5м от
поверхности. Построить эпюру напряжений
сжатия на горизонтальных площадках
(
.
Уровень грунтовых вод на глубине 1,5м от
поверхности. Построить эпюру напряжений
сжатия на горизонтальных площадках
(![]() ).
).
|
Решение:
|
- Песок под водой
испытывает взвешивающее действие
- Суглинок под
водой не испытывает взвешивающего
действия воды
- Супесь под водой испытывает взвешивающее действие воды
|
Пример 4.
Основание состоит
из суглинка
![]() ,
подстилаемого супесью
,
подстилаемого супесью![]() ,
подстилаемой слоем песка мелкого
,
подстилаемой слоем песка мелкого![]() .
Характеристики грунтов принять из
примера 4. Уровень грунтовых вод на
глубине 1,5м от поверхности. Построить
эпюру сжимающих напряжений
.
Характеристики грунтов принять из
примера 4. Уровень грунтовых вод на
глубине 1,5м от поверхности. Построить
эпюру сжимающих напряжений![]() от собственного веса грунта.
от собственного веса грунта.
Решение:
Суглинок не
подвержен взвешивающему действию
![]()
![]()
Супесь испытывает
взвешивающее действие воды
![]()
![]()
Песок мелкий
испытывает взвешивающее действие воды
![]()
![]()
|
|
Задание 7. Расчёт деформации грунтового основания под нагрузкой передаваемой штампом
Выполнить расчёт осадок и кренов штампов с прямоугольной и ленточной формой в плане при давлениях на грунт Pср ≤ R. Размеры подошвы и глубину заложения штампов принять из заданий 5 и 6. Грунтовые условия соответствуют заданной строительной площадке. Расчёты выполнить с применением модели линейно деформируемого полупространства по методу послойного суммирования.
Методы расчёта осадок грунтовых оснований с применением модели линейно-деформируемых тел.
Деформации сжатия
оснований под воздействием веса
возводимых сооружений принято называть
осадками. Различают осадки уплотнения,
развивающиеся при нагрузках, не
превышающих
![]() (начальное
критическое давление на грунт) и
пластические осадки при давлениях на
грунт
(начальное
критическое давление на грунт) и
пластические осадки при давлениях на
грунт![]() .
Осадки уплотнения определяются по
расчетным методикам с применением
решений теории линейно деформируемых
тел (ТЛДТ) с учетом особенностей грунтовой
среды как дисперсного тела. Осадки
пластические определяются с применением
методик, основанных на различных моделях,
учитывающих деформации пластичности
и ползучести. При проектировании
грунтовых оснований различных сооружений
по деформациям применяются решения по
модели ТЛДТ. Давление по подошве
фундаментов для практических расчетов
ограничивается величиной
.
Осадки уплотнения определяются по
расчетным методикам с применением
решений теории линейно деформируемых
тел (ТЛДТ) с учетом особенностей грунтовой
среды как дисперсного тела. Осадки
пластические определяются с применением
методик, основанных на различных моделях,
учитывающих деформации пластичности
и ползучести. При проектировании
грунтовых оснований различных сооружений
по деформациям применяются решения по
модели ТЛДТ. Давление по подошве
фундаментов для практических расчетов
ограничивается величиной![]() (расчетное
сопротивление грунта). Для расчетов
конечных (стабилизированных) осадок
уплотнения грунтовых оснований
применяются модели линейно деформируемого
полупространства (ЛДП), линейно
деформируемого слоя конечной толщины
(ЛДС).
(расчетное
сопротивление грунта). Для расчетов
конечных (стабилизированных) осадок
уплотнения грунтовых оснований
применяются модели линейно деформируемого
полупространства (ЛДП), линейно
деформируемого слоя конечной толщины
(ЛДС).
Расчет деформаций
грунтового основания с применением
модели ЛДП осуществляется с ограничением
глубины сжимаемой толщи (![]() )
по условию:
)
по условию:
![]()
![]() - напряжения в
грунте на глубине z
от передаваемой на грунт нагрузки;
- напряжения в
грунте на глубине z
от передаваемой на грунт нагрузки;
![]() - то же от собственного
веса грунта;
- то же от собственного
веса грунта;
![]() при модуле деформаций
грунта, залегающего у нижней границы
сжимаемой толщи
при модуле деформаций
грунта, залегающего у нижней границы
сжимаемой толщи
![]() ;
;
![]() при
при
![]() на границе сжимаемой толщи или ниже ее.
на границе сжимаемой толщи или ниже ее.
Модель линейно
деформируемого слоя (ЛДС) для расчета
осадок основания применяется в случае,
если в пределах сжимаемой толщи залегает
слой грунта с модулем деформации
![]() ,
толщиной
,
толщиной![]() :
:
![]()
![]() - модуль деформации
слоя грунта, подстилающего слой грунта
с модулем деформации
- модуль деформации
слоя грунта, подстилающего слой грунта
с модулем деформации
![]() .
.
Модель ЛДС
применяется также при размере площади
нагрузки
![]() при модуле деформаций в пределах
сжимаемой толщи
при модуле деформаций в пределах
сжимаемой толщи![]() ,
суммарная мощность слоев с
,
суммарная мощность слоев с![]() не должна превышать
не должна превышать![]() .
.
Определение модуля деформации грунта.
Для однородного основания, представленного одним грунтом для условий линейно-деформируемого полупространства величина конечной осадки может быть определена по зависимости:
![]()
![]() - интенсивность
равномерно распределенной дополнительной
нагрузки;
- интенсивность
равномерно распределенной дополнительной
нагрузки;
![]() - ширина, меньшая
сторона площади нагружения;
- ширина, меньшая
сторона площади нагружения;
![]() - коэффициент
Пуассона для грунта, принимается равным
для грунтов: крупнообломочных – 0,27;
песков и супесей – 0,30; суглинков -0,35;
глин – 0,42;
- коэффициент
Пуассона для грунта, принимается равным
для грунтов: крупнообломочных – 0,27;
песков и супесей – 0,30; суглинков -0,35;
глин – 0,42;
![]() - осадка штампа от
дополнительной нагрузки на грунт;
- осадка штампа от
дополнительной нагрузки на грунт;
![]() - коэффициент
влияния формы подошвы для модели работы
основание - ЛДП и влияния глубины
практически несжимаемого слоя грунта
для модели основание - ЛДС. Величины
- коэффициент
влияния формы подошвы для модели работы
основание - ЛДП и влияния глубины
практически несжимаемого слоя грунта
для модели основание - ЛДС. Величины
![]() приведены в таблице 7.1.
приведены в таблице 7.1.
Значения коэффициентов
![]() для
гибкой конструкции штампа
Таблица 7.1
для
гибкой конструкции штампа
Таблица 7.1
|
№ п/п |
Форма подошвы штампа-фундамента |
Глубина залегания
«скалы»,
|
Жесткость штампа | ||||
|
1,0 |
2,0 |
5,0 |
10,0 |
>10 | |||
|
1 |
Круг |
0,58 |
0,70 |
0,78 |
0,81 |
0,85 |
0,79 |
|
2 |
Прямоугольник
при
|
0,62 |
0,77 |
0,87 |
0,91 |
0,95 |
0,88 |
|
3 |
Прямоугольник
при
|
0,70 |
0,96 |
1,16 |
1,23 |
1,30 |
1,22 |
|
4 |
Прямоугольник
при
|
0,73 |
1,04 |
1,31 |
1,42 |
1,53 |
1,44 |
|
5 |
Прямоугольник
при
|
0,77 |
1,15 |
1,62 |
1,90 |
2,25 |
2,12 |
|
6 |
Полоса |
0,79 |
1,20 |
1,77 |
2,19 |
3,69 |
|
При проведении исследований грунтовых оснований для целей строительства приведенное решение по определению осадки применяется в штамповых испытаниях для определения модуля общей деформации грунта.
Расчет осадки основания по методу послойного суммирования с применением модели линейно деформируемого полупространства.
В практике
проектирования оснований зданий и
сооружений применяется метод послойного
суммирования для расчета осадок
фундаментов. Этот метод приводится в
нормативных документах. Для модели ЛДП
основание под площадью нагрузки
разбивается на условные слои
![]() ,
осадка которых определяется с применением
решения задачи одномерного обжатия
грунта:
,
осадка которых определяется с применением
решения задачи одномерного обжатия
грунта:
![]() ,
,
![]() - среднее напряжение
сжатия в i-м
слое грунта;
- среднее напряжение
сжатия в i-м
слое грунта;
![]() - модуль деформации
грунта i-го
слоя:
- модуль деформации
грунта i-го
слоя:
![]()
![]() - коэффициент
относительной сжимаемости грунта,
определяется по результатам компрессионных
испытаний;
- коэффициент
относительной сжимаемости грунта,
определяется по результатам компрессионных
испытаний;
![]() - коэффициент,
учитывающий боковые деформации грунта:
- коэффициент,
учитывающий боковые деформации грунта:
![]() ;
;
![]() - коэффициент
Пуассона для грунта.
- коэффициент
Пуассона для грунта.
Осадка грунта в уровне приложения нагрузки определяется как сумма осадок условно выделенных слоев в пределах сжимаемой толщи основания
![]()
|
|
НГСТ – нижняя граница сжимаемой толщи основания;
Напряжения в грунте определяются по осям, проходящим не через центр площади нагрузки. |
Расчет крена фундамента-штампа.
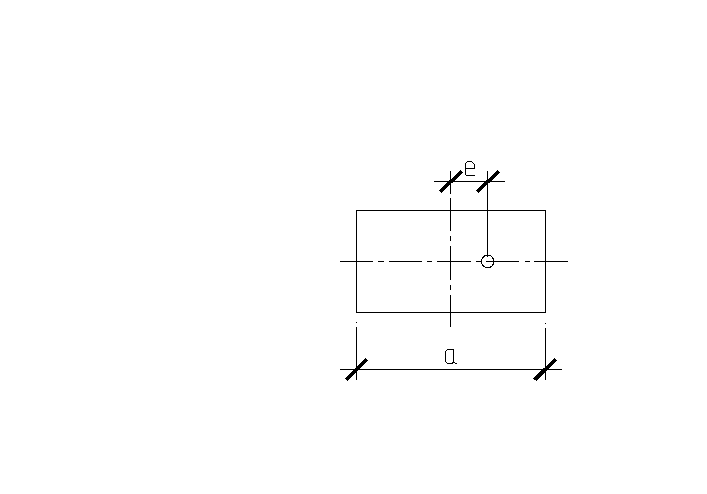
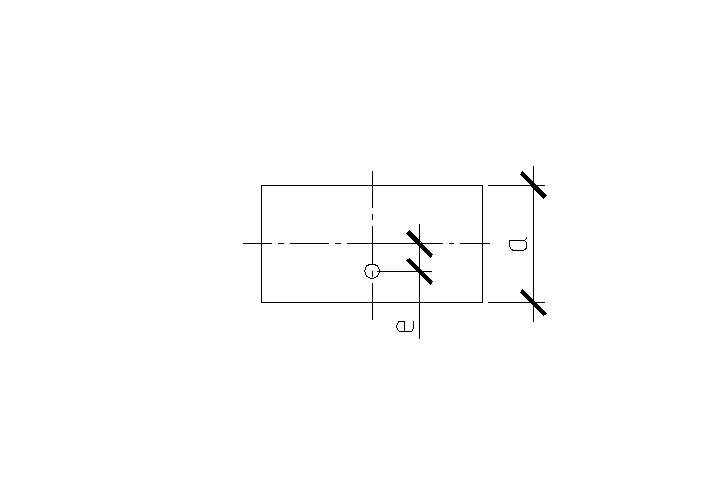
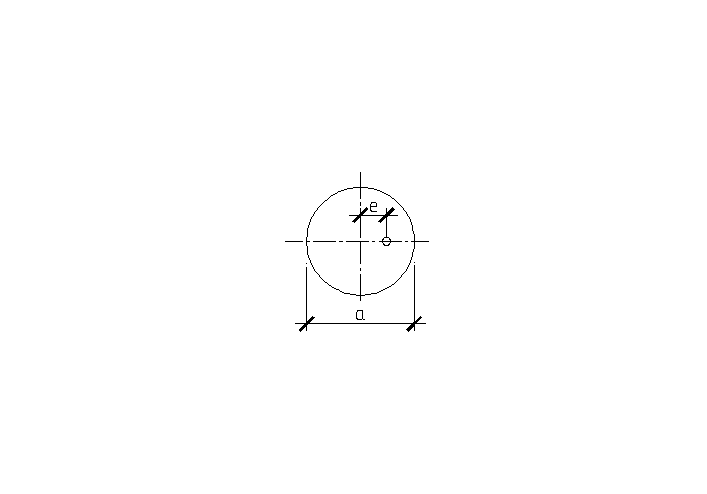
Деформации крена развиваются при действии внецентренной нагрузки. Давление на грунта под подошвой штампа изменяется с разгрузкой одного края и пригрузкой другого.
![]() ,
где е
– эксцентриситет приложения нагрузки;
,
где е
– эксцентриситет приложения нагрузки;
![]() -
для штампа с прямоугольной формой
подошвы;
-
для штампа с прямоугольной формой
подошвы;
![]() -
для ленточных штампов.
-
для ленточных штампов.
|
|
Для применимости
решений теории линейно-деформируемых
тел давление
|
![]() - коэффициент
влияния формы подошвы (
- коэффициент
влияния формы подошвы (![]() )
и глубины залегания несжимаемого слоя
грунта (
)
и глубины залегания несжимаемого слоя
грунта (![]() ),
принимается по таблице 7.3;
),
принимается по таблице 7.3;
![]() - коэффициент,
учитываемый при
- коэффициент,
учитываемый при
![]() и
и![]() ,
принимается по таблице 7.2
,
принимается по таблице 7.2
Таблица 7.2
|
Среднее значение E, кг/см2 |
Значения коэффициентов km при b, м | ||
|
|
|
| |
|
|
1 |
1 |
1 |
|
|
1 |
1,5 |
1,5 |
Таблица 7.3
|
Форма фундамента и направление действия момента |
|
Коэффициент ke при / = 2H/ b, равном | |||||||
|
0,5 |
1 |
1,5 |
2 |
3 |
4 |
5 |
| ||
|
Прямоугольник с моментом вдоль большей стороны
|
1 |
0,28 |
0,41 |
0,46 |
0,48 |
0,50 |
0,50 |
0,50 |
0,50 |
|
1,2 |
0,29 |
0,44 |
0,51 |
0,54 |
0,57 |
0,57 |
0,57 |
0,57 | |
|
1,5 |
0,31 |
0,48 |
0,57 |
0,62 |
0,66 |
0,68 |
0,68 |
0,68 | |
|
2 |
0,32 |
0,52 |
0,64 |
0,72 |
0,78 |
0,81 |
0,82 |
0,82 | |
|
3 |
0,33 |
0,55 |
0,73 |
0,83 |
0,95 |
1,01 |
1,04 |
1,17 | |
|
5 |
0,34 |
0,60 |
0,80 |
0,94 |
1,12 |
1,24 |
1,31 |
1,42 | |
|
10 |
0,35 |
0,63 |
0,85 |
1,04 |
1,31 |
1,45 |
1,56 |
2,00 | |
|
Прямоугольник с моментом вдоль меньшей стороны
|
1 |
0,28 |
0,41 |
0,46 |
0,48 |
0,50 |
0,50 |
0,50 |
0,50 |
|
1,2 |
0,24 |
0,35 |
0,39 |
0,41 |
0,42 |
0,43 |
0,43 |
0,43 | |
|
1,5 |
0,19 |
0,28 |
0,32 |
0,34 |
0,35 |
0,36 |
0,36 |
0,36 | |
|
2 |
0,15 |
0,22 |
0,25 |
0,27 |
0,28 |
0,28 |
0,28 |
0,28 | |
|
3 |
0,10 |
0,15 |
0,17 |
0,18 |
0,19 |
0,20 |
0,20 |
0,20 | |
|
5 |
0,06 |
0,09 |
0,10 |
0,11 |
0,12 |
0,12 |
0,12 |
0,12 | |
|
10 |
0,03 |
0,05 |
0,05 |
0,06 |
0,06 |
0,06 |
0,06 |
0,07 | |
|
Круглый |
- |
0,43 |
0,63 |
0,71 |
0,74 |
0,75 |
0,75 |
0,75 |
0,75 |
|
Примечание. При использовании расчетной схемы основания в виде линейно деформируемого полупространства коэффициент ke принимается по графе, соответствующей / = . | |||||||||









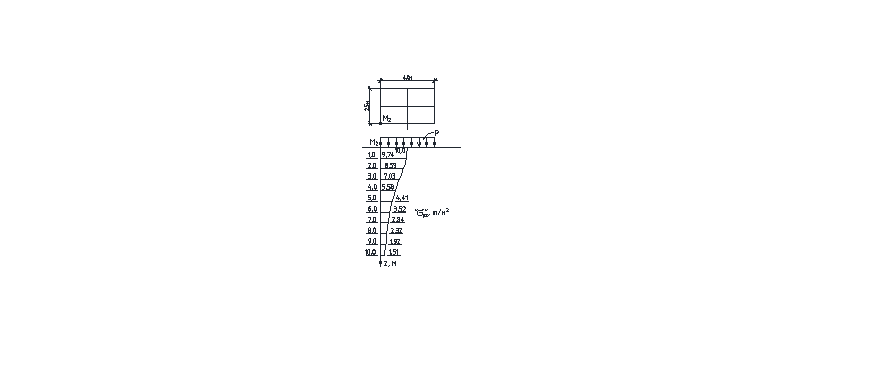







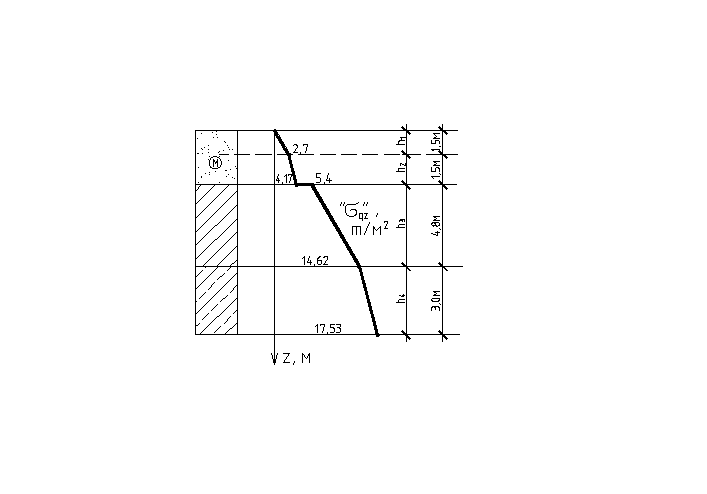
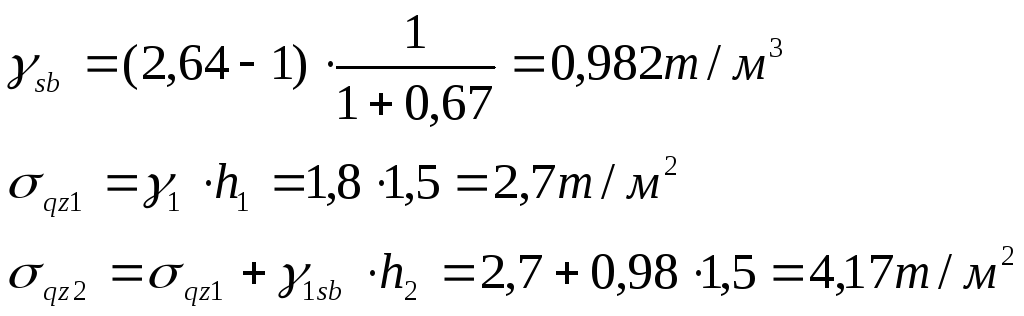


 Рис.7.1. Схема к
расчету осадок штампа-фундамента по
методу послойного суммирования
Рис.7.1. Схема к
расчету осадок штампа-фундамента по
методу послойного суммирования