суббота 29 Июнь, 2019
Колебания и волны. Геометрическая и волновая оптика
Кузнецов Сергей Иванович
доцент кафедры ОФ ЕНМФ ТПУ
Сегодня: суббота 29 Июнь, 2019
Тема 3.
ВЛИЯНИЕ ВНЕШНИХ СИЛ НА КОЛЕБАТЕЛЬНЫЕ ПРОЦЕССЫ
3.1 Свободные затухающие механические
колебания
3.2 Коэффициент затухания и логарифмический декремент затухания
3.3 Вынужденные механические колебания
3.4 Автоколебания
3.1 Свободные затухающие механические колебания
Все реальные колебания являются затухающими. Энергия механических колебаний постепенно расходуется на работу против сил трения и амплитуда колебаний уменьшается.
Сила трения (или сопротивления)
Fтр rυ
где r – коэффициент сопротивления, υ – скорость движения
Второй закон Ньютона для затухающих
прямолинейных колебаний вдоль оси x
max kx rυx
где kx – возвращающая сила, r x– сила трения.
|
d2 x |
|
r dx |
|
k |
x 0 |
|
|||||||||
|
dt2 |
|
|
|
|
|
|
|
|
|
||||||
|
m dt |
m |
|
|||||||||||||
|
|
|
|
|
|
|
||||||||||
Введем обозначения |
|
|
|
r |
|
|
β; |
|
|
k |
ω02 |
|||||
|
|
|
|
|
|
|
m |
|||||||||
|
|
2m |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
d2 x |
2β |
dx |
|
|
|
2 |
|
|
|
|
(3.1.1) |
||||
|
dt2 |
dt |
ω0 x 0 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение уравнения (3.1.1) имеет вид (при β ω0)
Решение уравнения (3.1.1) имеет вид
|
|
|
|
x A0e βt cos(ωt φ) |
|
|
|
|
|
(3.1.2) |
|||||||||
Найдем частоту колебаний |
ω. |
(ω ω0 ) |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β ω0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
ω ω02 β2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
r 2 |
||
|
|
k |
|
|
|
|
r |
|
|
|
|
|
|
||||||
ω0 |
; |
β |
; |
|
ω |
|
|
|
|
. |
|||||||||
|
m |
|
|||||||||||||||||
m |
2m |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2m |
||||||
условный период |
|
|
|
|
|
|
T 2π |
|
|
2π |
|
, |
|
|
|
|
|
|||
|
ω |
|
|
|
|
|
|
|
|
ω02 β2 |
|
|
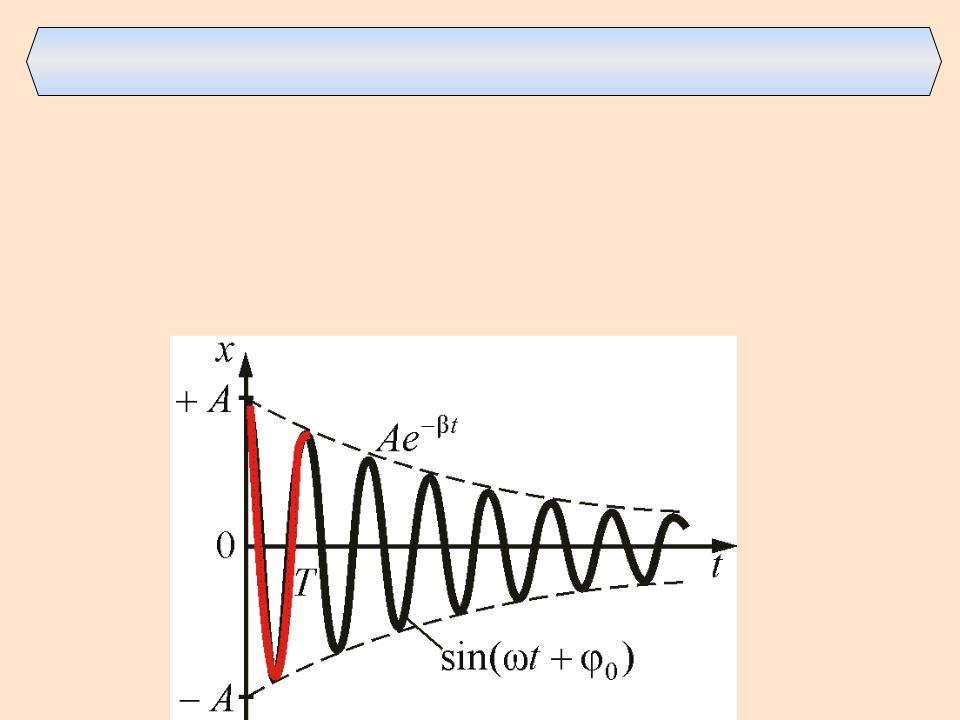
3.2 Коэффициент затухания и логарифмический декремент затухания
A(t) |
|
A0e βt |
βT |
|
|
|
|
e |
|
A(t T ) |
A e β(t T ) |
|
||
|
0 |
|
|
|
где β – коэффициент затухания
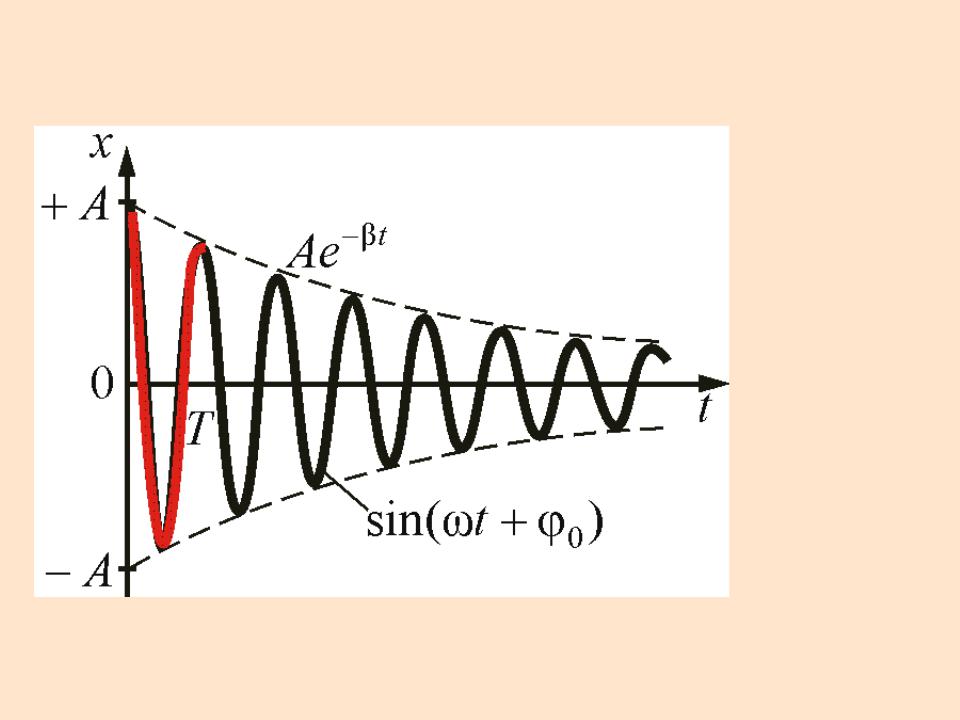
Рисунок 1
Логарифмическим декрементом затухания называется натуральный логарифм отношения
амплитуд, следующих друг за другом через период Т.
|
|
|
A(t) |
|
|
|
|
|
|
||
|
|
|
|
βT |
|
; |
χ βT |
||||
χ ln A(t T ) ln e |
|
βT |
|||||||||
|
|
|
|
||||||||
|
A0 |
|
|
βτ |
1 |
, откуда βτ 1; |
1 |
||||
|
|
e |
|
e |
β τ . |
||||||
|
A |
|
|||||||||
|
τ |
|
|
|
|
|
|
|
|
|
|
Следовательно, коэффициент затухания β – есть физическая величина, обратная времени, в течение
которого амплитуда уменьшается в е раз, τ – время релаксации.
χβT
β1τ .
Когда сопротивление становится равным критическому r rкр , а β ω0 , то круговая частота обращается в нуль (ω 0), ( T ), колебания прекращаются. Такой процесс называется
апериодическим:
r rкр
β ω0 ω 0
T
Рисунок 2