
- •1.1. Численное дифференцирование
- •1.1.1. Первая производная. Двухточечные методы
- •1.1.2. Вычисление первых производных по трёхточечным схемам
- •1.1.3. Вычисление производных второго порядка
- •1.1.4. Вычисление производных третьего порядка
- •1.2. Решение нелинейных уравнений
- •1.3.1. Метод Эйлера
- •1.3.2. Метод Рунге-Кутта
- •1.3.3. Модифицированный метод Эйлера
- •1.4. Численное решение системы дифференциальных уравнений
- •1.6. Введение в операторный метод
- •1.6.1. Преобразование Карсона-Хевисайда
- •1.6.2. Изображение по Лапласу
- •1.6.3. Некоторые формулы соответствия оригинала изображению
- •1.6.4. Изображение интеграла
- •1.6.6. Первый закон Кирхгофа в операторной форме
- •1.6.7. Второй закон Кирхгофа в операторной форме
- •1.6.8. Последовательность расчета в операторном методе
- •1.6.9. Аналогия с переменным током
- •1.7.1. Переход от изображения к функции времени
- •1.7.2. Методы разложения
- •2.1. Введение
- •2.2.1. Основные выражения
- •2.2.5. Разряд конденсатора в цепи RLC.
- •2.2.6. Воздействие постоянного напряжения на RCL - цепь
- •3.1.1. Принцип создания электротехнических блоков пользователя
- •3.2.2. Блок S-function
- •3.2.3. Математическое описание S-функции
- •3.2.4. Этапы моделирования
- •3.2.5. Callback-методы S-функции
- •3.2.6. Основные понятия S-функции
- •3.2.7. Создание S-функций на языке MATLAB
- •3.2.8. Примеры S-функций языке MATLAB
- •4. ЗАДАНИЯ НА ВЫПОЛЕНИЕ ЛАБОРАТОРНЫХ РАБОТ
- •4.1.1. Моделирование и исследование процессов в RC–цепи
- •4.1.5. Заряд емкости
- •4.1.6. Разряд емкости
- •4.1.8. Разряд индуктивности
- •4.1.9. Моделирование полупроводникового диода

|
|
|
|
|
|
|
|
|
4.1.5. Заряд емкости |
|
|
, |
||||||||
|
Цель лабораторной работы |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проанализировать процесс заряда емкости в RC-цепи с применением |
|||||||||||||||||||
математических моделей, полученных при помощи различных методов |
||||||||||||||||||||
решения уравнений в системе MATLAB и среде MATLAB Simulink. |
У |
|||||||||||||||||||
|
Основные выражения |
|
|
|
|
|
|
|
|
|
П |
|
||||||||
|
Рассмотрим схему, показанную на рис. 6.10. |
Т |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Н |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
. |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Н |
|
|
|
. |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
Рис. 6.10. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ю |
|
|
|
После замыкания ключа S в данной цепи начинается переходный |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
Э |
|
|
|
|
|
|
|
|
|
||
процесс по заряду емкости С. Замыкание ключа происходит в момент |
||||||||||||||||||||
времени t = 0. |
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Исходя из допущения, что к ммутация происходит мгновенно и |
|||||||||||||||||||
|
|
|
|
|
О |
|
|
|
в |
|
|
|
|
|||||||
обозначив время непосредстве |
|
перед коммутацией t(0−) , а время |
||||||||||||||||||
сразу после коммутации t(0+ ) , |
|
|
|
записать: |
t(0−) =t(0+ ) . В даль- |
|||||||||||||||
|
|
|
|
Э |
|
мож |
|
|
|
|
|
|
|
|||||||
нейшем все параметры токов и апряжений в схеме непосредственно |
||||||||||||||||||||
перед коммутацией будем обозначать подстрочным индексом (−) , а сра- |
||||||||||||||||||||
|
|
П |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
зу после коммутации (+ )с. |
|
|
|
|
|
|
|
|
|
|||||||||||
|
Определим нач льные условия схемы: I (0−) = 0,UC (0−) =U0. |
|
|
|||||||||||||||||
|
Э |
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Сразу после коммутации схема будет выглядеть следующим обра- |
|||||||||||||||||||
. |
|
|
р |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ц |
|
|
К |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
зом (рис. 6.11).
Рис. 6.11.
111
|
|
Составим уравнение по второму закону Кирхгофа для цепи сразу |
||||||||||||||||||||||||
|
после коммутации |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
UR +UС = E |
|
|
|
|
|
П |
, |
|||||||||
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Ri +UС = E . |
|
Н |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dUC |
|
||||
|
|
Запишем значение тока, протекающего через емкостьТкак i = C |
, |
|||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
dt |
|
|
||||
|
тогда последнее уравнение можно переписать в виде: |
Ю |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
RC |
dUC |
|
+UC = E.; |
|
|
|
. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
. |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Э |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
||
|
|
Из теории решения линейных дифференциальных уравнений из- |
||||||||||||||||||||||||
|
вестно что: |
|
|
О |
|
|
|
Н |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
|||||||
|
|
Решение неоднородного уравнения, удовлетворяющее заданным на- |
||||||||||||||||||||||||
|
чальным условиям, всегда следует искать |
|
иде суммы какого-либо ча- |
|||||||||||||||||||||||
|
|
|
|
|
Э |
|
|
|
|
о |
|
|
|
|
|
|
|
|
||||||||
|
стного решения этого неоднородного ура нения и общего решения со- |
|||||||||||||||||||||||||
|
ответствующего однородного ура нения, у которого правая часть |
|||||||||||||||||||||||||
|
|
|
П |
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
равна 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
В нашем случае зависимость uC(t) будет иметь две составляющих: |
|
|
||||||||||||||||||||||
|
Э |
|
|
|
|
|
u |
(t) =U |
|
+U |
C |
; |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
CнC |
|
|
|
|
|
|
|
|
|
||||||||
. |
|
|
|
р |
|
|
|
|
|
|
|
ПР |
|
СВ |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
– принужденное зн чение напряжения. Определяется для момента |
||||||||||||||||||||||||||
ц |
UC |
|
||||||||||||||||||||||||
|
ПР |
|
К |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
времени t = ∞, |
то естьапо окончании переходного процесса. При E = |
||||||||||||||||||||||||
о |
const, UCПР =E. |
|
|
|
|
|
|
|
|
|
|
|
|
UC |
представляет из себя |
|||||||||||
|
Свободная |
составляющая напряжения |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
СВ |
|
|
|
|
|
|
|
|
сумму экспонент типа Ak e |
pkt |
; Для нашего случая (с одним накопителем |
|||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
энергии) это только одна экспонента:
UCСВ = Aept .
Тогда общее решение уравнения будет иметь вид: 112

uC (t) = E + Aept ,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
где А – постоянная интегрирования, определяемая из начальных усло- |
|||||||||||||||||||||||||||||||||
|
вий, p – корень характеристического уравнения. |
|
|
|
П |
, |
||||||||||||||||||||||||||||
|
|
Представим исходное дифференциальное уравнение в виде изобра- |
||||||||||||||||||||||||||||||||
|
жения по Лапласу, заменив |
d |
|
→ p и получим: |
|
|
|
|
|
|
||||||||||||||||||||||||
|
dt |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Н |
|
. |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
RCp +1 = 0 , откуда: p = − |
|
|
1 |
; |
Т |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
RC |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
||||||||||
|
|
Исходя из второго закона коммутации можно записать: |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Н |
|
|
|
|
|
|
|
|
|
|
|
Ю |
|
|
||||||
|
|
|
|
|
|
|
|
|
UC (0−) |
=UC |
(0+ ), |
|
|
|
|
|
|
|
|
. |
|
|
|
|||||||||||
|
|
Пусть емкость C была изначально заряжена до величины U0, тогда |
||||||||||||||||||||||||||||||||
|
для времени t = 0 имеем: |
|
Э. |
вRC |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
О |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
U0 = E + A |
, откуда: |
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
||||||||||||||||
|
|
Э |
A =U0 |
– E |
о |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
Окончательное решение запишем |
|
иде: |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
u(t) = E + (U0 − E)e |
− |
1 |
|
t |
|
, |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
или: |
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
ЭUC |
|
|
а |
н− 1 t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
П |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
u(t) =U |
e |
pC |
+ E(1−e−RC t ). |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ц |
Если |
К |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
(0) = 0, т.е. емкость была не заряжена, решение будет выгля- |
|||||||||||||||||||||||||||||||
.деть следующемроб азом: |
|
|
|
|
|
|
|
|
− 1 t |
).. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
U (t) = E(1−e |
|
RC |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Величина |
RC =τ – |
называется постоянной времени. Принято счи- |
||||||||||||||||||||||||||||||
|
тать, что переходный процесс завершается через время t = (3 ÷5)τ. . |
|
||||||||||||||||||||||||||||||||
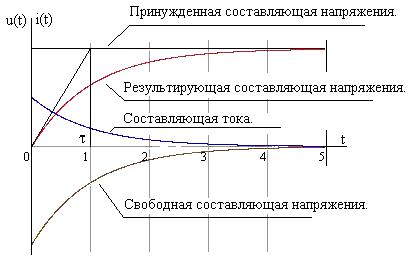
На рис. 6.12 дана графическая интерпретация переходных процессов в схеме.
113
|
|
|
Для того, чтобы определить ток, протекающий через конденсатор |
||||||||||||||||||||
|
необходимо решить уравнение вида: |
|
|
|
|
|
|
|
|
У |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dUC |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
i = C |
. |
|
|
|
П |
, |
|||||||
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Н |
. |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Н |
|
|
|
Ю |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
||||||||
|
|
|
|
|
|
|
О |
Э |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
||||||||||
|
|
|
|
|
Э |
|
|
|
Рис. 6.12. |
|
|
|
|
|
|
|
|||||||
|
|
|
На графике эта зависимость показана, как «ИСоставляющая тока». |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
точки |
|
|
|
|
|
|
|||||
|
|
|
Постоянную времени τ |
|
можно |
пределить графически. Для этого |
|||||||||||||||||
|
|
|
|
П |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
проведем касательную к началу фу кции U(t) до ее пересечения с при- |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
рис |
|
|
|
|
|
|
пересечения на ось времени |
||||||||
|
нужденной составляющей. Проекция |
|
|
|
|
||||||||||||||||||
|
|
Э |
|
|
а |
|
. 6.12). |
|
|
|
|
|
|
|
|
|
|||||||
|
даст численное значение τ |
( |
|
|
|
|
|
|
|
|
|
|
|||||||||||
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ц |
|
Задание к выполнению л бораторной работы |
|
|
|
|
|||||||||||||||||
|
По структу ной схеме (рис. 6.10) и заданным уравлениям изучить |
||||||||||||||||||||||
о |
1 |
|
|||||||||||||||||||||
|
|
принцип функционированияр |
электрической цепи. |
|
|
|
|
||||||||||||||||
|
2. Определить |
входные и |
выходные переменные цепи, как объекта |
||||||||||||||||||||
|
|
|
управленияК. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3. Определить вектора входных, состояния, и выходных переменных |
||||||||||||||||||||||
|
4. |
системы, а также матрицы параметров в пространстве состояний. |
|
||||||||||||||||||||
|
Записать передаточную функцию преобразования сигналов. |
|
|
||||||||||||||||||||
|
5. |
Исследовать построенную систему на устойчивость с помощью кри- |
|||||||||||||||||||||
|
|
|
терия Гурвица и критерия Ляпунова. |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
114 |
|
|
|
|
|
|
|
|
|
|
|
