
Расчет монохроматора
.docCoolReferat.com
1. РАСЧЕТ МОНОХРОМАТОРА
1.1. Габаритный расчет
1.1.1. Исходные данные
Вариант № 1.
Рассчитаем монохроматор для следующих условий:
спектральная
область,
![]() =
(300 - 800) нм,
=
(300 - 800) нм,
обратная
линейная дисперсия,
![]() =
8
нм/мм,
=
8
нм/мм,
фокусные
расстояния сферических зеркал
![]() =
300 мм
=
300 мм
1.1.2. Выбор оптической схемы.
Для обеспечения работы в широком диапазоне длин волн при относительно небольших габаритах прибора выгодно использовать оптическую схему монохроматора, построенную по схеме Эберта-Фасти. В качестве диспергирующего элемента применяем дифракционную решётку.

Рис. 1.1.
![]() и
и
![]() - входная
и выходная щели,
- входная
и выходная щели,
![]() и
и
![]() -
объективы,
-
объективы,
![]() и
и
![]() - поворотные
зеркала,
- поворотные
зеркала,
![]() -
диспергирующий
элемент,
-
диспергирующий
элемент,
![]() -
фильтр.
-
фильтр.
1.1.3. Общие соотношения для дифракционной решетки
Распределение интенсивности света дифрагированного решеткой
определяется выражением [I]
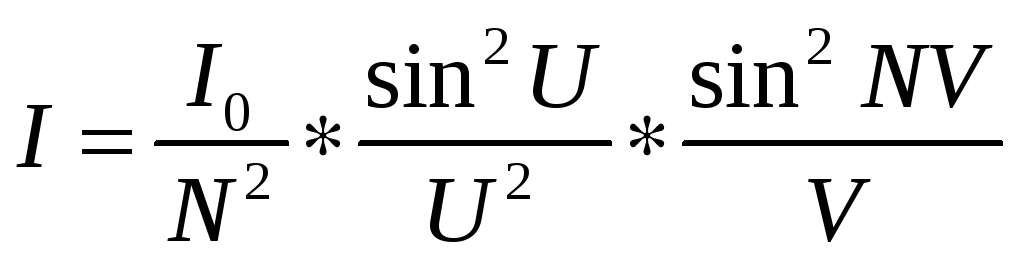 (1.1)
(1.1)
Где ![]() - интенсивность
падающего
света,
- интенсивность
падающего
света,
![]() -
число
штрихов решетки,
-
число
штрихов решетки,
 -
множитель,
определяющий дифракцию от каждого
элемента решётки.
-
множитель,
определяющий дифракцию от каждого
элемента решётки.
При этом
 (1.2)
(1.2)
![]() -
ширина
рабочей грани штриха,
-
ширина
рабочей грани штриха,
![]() -
рабочая
длина волны,
-
рабочая
длина волны,
![]() -
угол
падения,
-
угол
падения,
![]() -
угол
дифракции,
-
угол
дифракции,
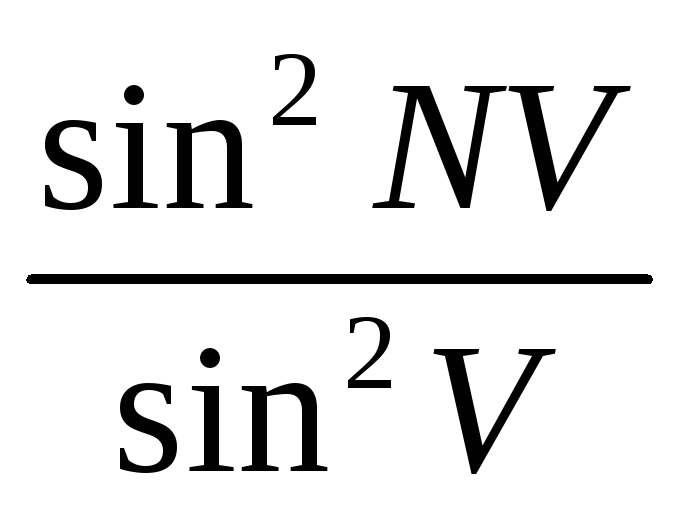 -
множитель,
определяющий положение главных
дифракционных максимумов.
-
множитель,
определяющий положение главных
дифракционных максимумов.
 (1.3)
(1.3)
![]() -
постоянная
решетки.
-
постоянная
решетки.
Интенсивность
![]() = 0, если второй или третий член в формуле
(1.1) равен нулю. Для второго члена (1.2)
минимум будет иметь место при условии
= 0, если второй или третий член в формуле
(1.1) равен нулю. Для второго члена (1.2)
минимум будет иметь место при условии
![]() ,
где
,
где
![]() =
1, 2…
=
1, 2…
т.е.
когда
![]() ,
,
![]()
Так
как "![]() "
очень мало, минимумы, определяемые этим
множителем,
"
очень мало, минимумы, определяемые этим
множителем,
редкие. За счёт третьего множителя (1.3) образуются частые минимумы
вследствие большого количества штрихов N.
Условие минимумов определяется соотношением
![]()
При
этом
![]() - принимает значение целых чисел, кроме
значений кратных N
,
т.е. кроме значений
- принимает значение целых чисел, кроме
значений кратных N
,
т.е. кроме значений
![]() = 0, N
,
2 N
... mN.
= 0, N
,
2 N
... mN.
В
этих случаях
![]() ,
третий множитель принимает значение,
равное
,
третий множитель принимает значение,
равное
![]() и вместо минимумов появляются главные
максимумы, интенсивность которых
определяется соотношением:
и вместо минимумов появляются главные
максимумы, интенсивность которых
определяется соотношением:
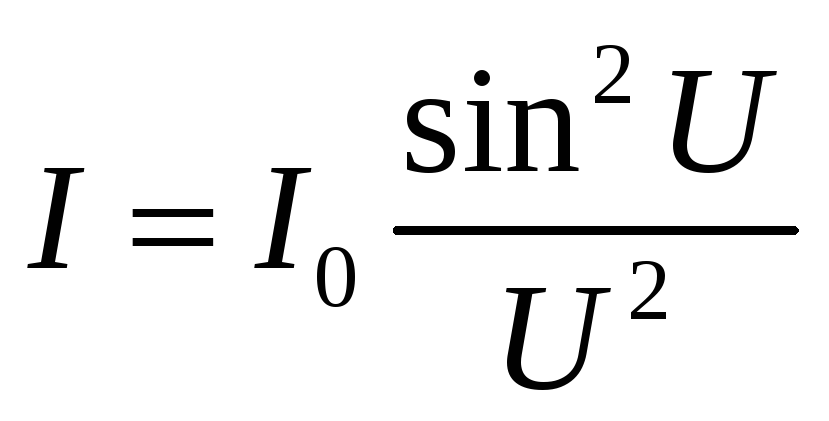 (1.4)
(1.4)
Формула решетки для условия главных дифракционных максимумов определяется выражением:
![]() (1.5)
(1.5)
где
m
=
![]() 1,
2, 3....
1,
2, 3....
Каждому значению m соответствует спектр m-го порядка.
1.1.4. Основные характеристики решетки
Из
формулы (1.5) после дифференцирования по
![]() непосредственно следует выражение
для угловой дисперсии
непосредственно следует выражение
для угловой дисперсии
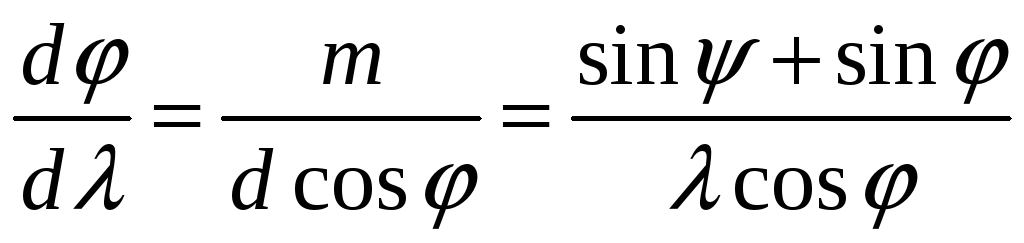 (1.6)
(1.6)
Из
(1.6) видно, что для данной длины волны
угловая дисперсия в основном
определяется углом дифракции
![]() (при условии, что угол падения
(при условии, что угол падения
![]() остается
постоянным).
остается
постоянным).
Свободный
спектральный интервал между налагающимися
длинами волн соседних порядков
определяется при выбранных
![]() и
и
![]() соотношением
соотношением
 (1.7)
(1.7)
Разрешающая способность решетки при заданных углах падения и дифракции, может быть повышена только за счет увеличения размеров решетки. Это следует из соотношения [I]
 (1.8)
(1.8)
где
![]() - полное
сечение дифрагированного пучка.
- полное
сечение дифрагированного пучка.
1.1.5. Выбор параметров основных элементов монохроматора
Так
как заданная дисперсия прибора
относительно невысока выбираем
стандартную решетку-реплику с 600 штр/мм,
работающую в первом левом порядке
[I].
Размеры решетки 50х60
![]() (заштрихованной части), толщина 15 мм,
диаметр заготовки 90 мм. Решетку
устанавливаем в параллельном пучке,
в этом случае она практически не вносит
искажения изображения.
(заштрихованной части), толщина 15 мм,
диаметр заготовки 90 мм. Решетку
устанавливаем в параллельном пучке,
в этом случае она практически не вносит
искажения изображения.
В
качестве объективов выбираем два
сферических зеркала с фокусными
расстояниями в соответствии с заданием
![]() =
300 мм, диаметром
=
300 мм, диаметром
![]() =
60 мм. Фокусное расстояние в значительной
мере определяет значение светосилы
и линейной дисперсии.
=
60 мм. Фокусное расстояние в значительной
мере определяет значение светосилы
и линейной дисперсии.
Выбираем
угол между падающим и отраженным от
зеркального объектива
![]() центральными лучами, идущими от центра
входной щели к центру решетки
центральными лучами, идущими от центра
входной щели к центру решетки
![]() =
15°.
=
15°.
Угол
между центральными падающим и
дифрагированным от решетки лучами
принимаем
![]() =35°.
=35°.
Апертура монохроматора определяется
![]()
Где
![]() -
диаметр сферического зеркала
-
диаметр сферического зеркала

Угол
падения
![]() и
угол дифракции
и
угол дифракции
![]() (рис.
1.2.) связаны соотношением
(1.5)
(рис.
1.2.) связаны соотношением
(1.5)
 (1.9)
(1.9)

Рис. 1.2.
В
монохроматоре при изменении длины волны
углы
![]() и
и
![]() изменяются
одновременно, но их разность
изменяются
одновременно, но их разность
![]() остается постоянной.
остается постоянной.
После преобразования формула (1.9) приводится к виду
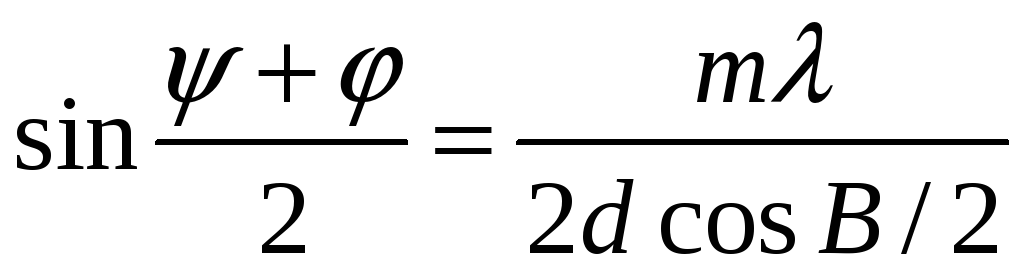 (1.10)
(1.10)
Для определения правильного положения дифракционной решетки произведем расчет для середины рабочего диапазона, а затем для крайних длин волн, что позволит определить угол поворота решетки.
Примем:![]() нм;
нм;
![]() =
300 нм;
=
300 нм;
![]() =800
нм.
=800
нм.
Учитывая,
что
![]() мм;
мм;
![]() ;
;
![]() =
15°;
=
15°;
![]() -
определим углы
-
определим углы
![]() и
и
![]() для
длины
волны
для
длины
волны
![]() нм
нм

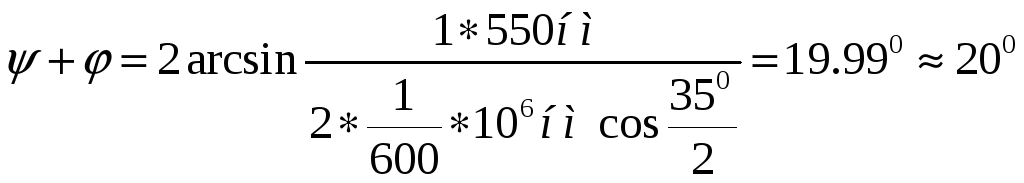
Имеем систему уравнений
![]()
![]()
Из ее решения получим
![]() ;
;
![]()
Меридиональное увеличение будет

и
![]()
Угол
между нормалью к поверхности дифракционной
решетки и оптической осью определяет
угол поворота решетки для различных
длин волн. Угол поворота решетки
![]() от
начального положения определится, из
соотношения
от
начального положения определится, из
соотношения

Для
![]() =
300 hm
=
300 hm

![]()
Для
![]() =
800
hm
=
800
hm

![]()
Для последовательного выведения всего спектра на щель необходимо повернуть решетку на угол
![]()
Считаем,
что входная щель помещена в меридиональном
астигматическом фокусе зеркального
объектива
![]() ,
а выходная в фокальной плоскости
коллиматорного объектива
,
а выходная в фокальной плоскости
коллиматорного объектива
![]() .
.
Тогда,
расстояние входной щели от зеркального
объектива
![]() определится из соотношения
определится из соотношения
 =
300•
0,9914 = 297,42
мм
=
300•
0,9914 = 297,42
мм
А
расстояние от выходной щели до объектива
![]() будет
будет
 =
300
• 0,984 = 295,2
мм
=
300
• 0,984 = 295,2
мм
1.1.6. Расчет характеристик монохроматора
Линейная дисперсия

Обратная линейная дисперсия

Ширина спектра

![]() (800
- 300)
нм = 102
мм
(800
- 300)
нм = 102
мм
Разрешающая способность определяется параметрами дифракционной решетки, расстоянием ее до сферических зеркал и шириной входной щели. Параметры решетки известны. Ширина входной щели определяется соотношением
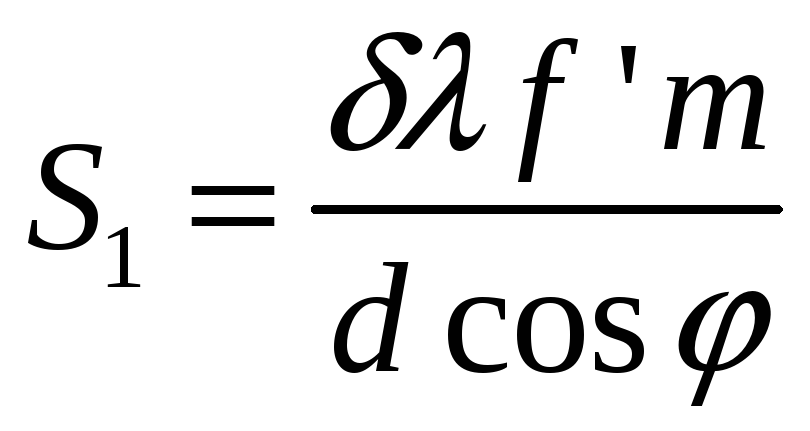
где
![]() -
требуемое
разрешение.
-
требуемое
разрешение.
Рассчитаем
ширину щели, задаваясь
![]() в
пределах от 1 до 8 нм (таблица 1.1.)
в
пределах от 1 до 8 нм (таблица 1.1.)
Таблица 1.1.
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0.2 |
0.4 |
0.6 |
0.8 |
1.01 |
1.21 |
1.42 |
1.62 |
Для ориентировочного определения ширины щели и разрешающей способности проведем приближенный расчет аберрационного пятна, ширина которого "b", зависит от ширины решетки (60 мм) и фокусного расстояния сферического зеркала

Ширина щели должна быть больше аберрационного пятна, т.е. в соответствии с данными таблицы 1.1. можно получить разрешение порядка 1 - 2 нм.
Уточним значение кружка рассеяния, обусловленного сферическими аберрациями.
Обозначим
через
![]() и
и
![]() координаты лучей в плоскости
перпендикулярной дифрагированному
пучку и проходящей через центр решетки
координаты лучей в плоскости
перпендикулярной дифрагированному
пучку и проходящей через центр решетки
f’ - фокусное расстояние зеркала,
L - расстояние точки изображения входной щели от горизонтальной
плоскости симметрии,
![]() и
и
![]() -
углы между падающими и отраженными от
зеркал главными лучами, идущими от
центра входной щели
-
углы между падающими и отраженными от
зеркал главными лучами, идущими от
центра входной щели
![]() к
центру
выходной щели
к
центру
выходной щели
![]() .
.
Составляющие аберраций 3-го порядка в направлении дисперсии определяются выражением
![]() (1.11)
(1.11)
Где
![]() - меридиональное
увеличение решетки,
- меридиональное
увеличение решетки,
![]() и
и
![]() -
координаты лучей в плоскости,
перпендикулярной дифрагированному
пучку и проходящей через центр решетки.
-
координаты лучей в плоскости,
перпендикулярной дифрагированному
пучку и проходящей через центр решетки.
Для сферических зеркал коэффициенты аберраций 3-го порядка равны
![]() ;
;
 ;
;
 ;
;
![]() ;
;
где x -расстояние от решетки до зеркал.
Из
аберраций 3-го порядка в монохроматоре
со сферическими зеркалами наибольшую
роль играет сферическая аберрация,
определяемая коэффициентом
![]() .
Формула
для аберрации децентрировки для случая,
когда входная щель помещена в меридиональном
астигматическом фокусе коллиматорного
объектива
.
Формула
для аберрации децентрировки для случая,
когда входная щель помещена в меридиональном
астигматическом фокусе коллиматорного
объектива
![]() имеет
вид [2].
имеет
вид [2].
 (1.12)
(1.12)
Расчет
![]() и
и
![]() по
формулам (1.11) и (1.12)
позволяет
уточнить полученные ранее значения
разрешения и ширины щели.
по
формулам (1.11) и (1.12)
позволяет
уточнить полученные ранее значения
разрешения и ширины щели.
1.1.7. Устранение наложения спектров
Из соотношения

следует,
что в области спектра от 400 до 600 нм
происходит наложение спектра 2-го
порядка от
![]() =
400нм/2
= 200 нм до
=
400нм/2
= 200 нм до
![]() =600нм/
2= 300 нм.
=600нм/
2= 300 нм.
Для устранения наложения порядков в этой области введем светофильтр БС 10, который не пропускает эту часть спектра.
Для
области 600 - 800 нм наложение спектров
второго порядка будет от
![]() =
600/2
= 300 нм до
=
600/2
= 300 нм до
![]() =
800/2 = 400 нм.
=
800/2 = 400 нм.
Для устранения порядков в этой области используем светофильтр КС 10.
1.1.8. Расчет осветительной системы
При выборе осветителя основное внимание следует уделить подбору источника света и способа освещения щели.
В заданном рабочем диапазоне (300 - 800 нм) можно использовать галогенную лампу КИМ-10-90, обладающую более высокой стабильностью в ультрафиолетовой области спектра по сравнению с ртутными лампами. Окончательный выбор источника света будет проведен на основе энергетического расчета.
Для освещения щели используем конденсор с минимальными хроматическими аберрациями.
Проведем габаритный расчет конденсора.

Рис.1.3.
Из конструктивных соображений принимаем расстояние от нити накала лампы до щели монохроматора равным 120 мм.
Конденсор
обеcпечивает
эффективное действие при увеличении
![]() .
Принимаем
.
Принимаем
![]() .
.
Фокусное расстояние конденсора определяется из решения системы уравнений

![]()
![]() и
учитывая, что - S
+
и
учитывая, что - S
+
![]() = 120
мм, получим
= 120
мм, получим
![]() =
120 мм. Откуда S
= 33,85 мм и
=
120 мм. Откуда S
= 33,85 мм и
![]() =86,15
мм.
=86,15
мм.
Фокусное расстояние конденсора

Для
равномерного освещения щели и согласования
апертур монохроматора и осветителя
выбираем угол охвата конденсора в
диапазоне
![]() =
=
![]()
Пусть
![]() =
40°,
тогда световой диаметр будет равен
=
40°,
тогда световой диаметр будет равен
![]()
Относительное отверстие конденсора
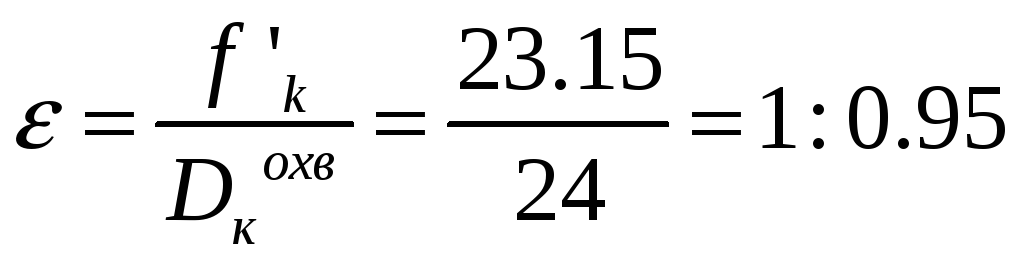
При полученном относительном отверстии, угле охвата, увеличении и фокусном расстоянии хорошее качество изображения дает конденсор, состоящий из двух плосковыпуклых линз.
По
каталогу подбираем двухлинзовый
конденсор из стекла КУ, с фокусным
расстоянием близким к требуемому. Для
конденсора с
![]() =
25,18 м на рис. 1.4 показаны уточнённые
значения геометрических размеров
=
25,18 м на рис. 1.4 показаны уточнённые
значения геометрических размеров
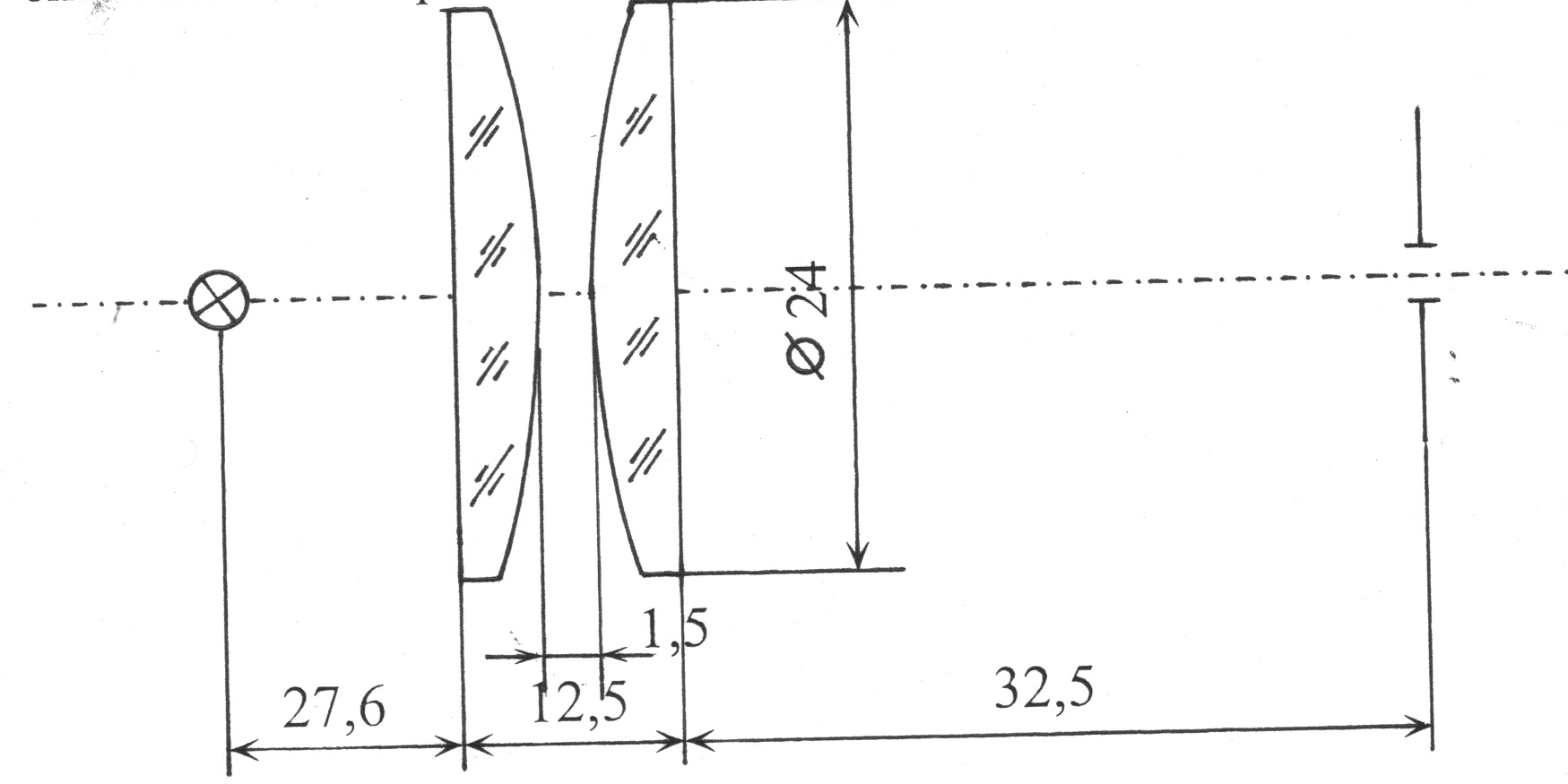
Рис. 1.4.
1.2. Энергетический расчет
1.2.1. Оптическая схема и исходные данные для расчета

Рис. 1.5.
1 - источник света, КИМ-10-90,
2 - конденсор двухлинзовый, стекло КУ, толщина по оси каждой линзы 5,5 мм,
3 - входная щель, в соответствии с габаритным расчетом монохроматора размеры щели 0,3х14м,
4 - отражающие сферические зеркала, выбираем покрытие марки 1И21Е,
5 - отражающие плоские зеркала, выбираем покрытие марки 1И21Е,
6 - дифракционная решетка, параметры ее приведены в разделе 3.1.4.
7
- светофильтр отрезающий, принимаем
коэффициент пропускания
![]() = 0.89
= 0.89
8 - выходная щель, размеры щели 0,3х14 мм.
1.2.2. Расчет светового потока на выходе оптической системы
Для
лампы КИМ-10-90 полный световой поток
![]() равен
1980 лм.
В
приборе используется часть светового
потока
равен
1980 лм.
В
приборе используется часть светового
потока
![]() ,
заключенного внутри телесного угла
,
заключенного внутри телесного угла
![]() опирающегося
на световой диаметр конденсора
опирающегося
на световой диаметр конденсора
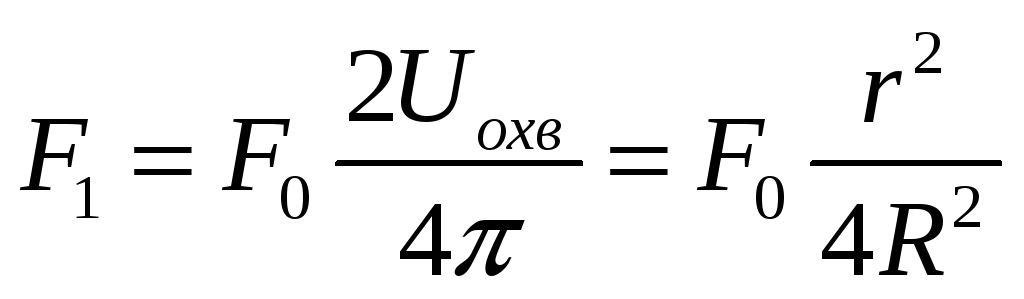 (1.13)
(1.13)
где
![]() -
радиус конденсора,
-
радиус конденсора,
![]() =
12 мм,
=
12 мм,
![]() -
расстояние от источника до конденсора
-
расстояние от источника до конденсора
R
= 27,6
мм![]()

Учитывая
потери в оптической системе
![]() ,
световой поток на выходе оптической
системы определится из соотношения
,
световой поток на выходе оптической
системы определится из соотношения
![]() (1.14)
(1.14)
Потери в данной оптической системе определяются:
а) Потерями на отражение от поверхностей деталей на границе воздух-стекло
![]() (1.15)
(1.15)
где
![]() -
число деталей с коэффициентами отражения
-
число деталей с коэффициентами отражения
![]() ,
,![]()
Коэффициент отражения для полированных оптических деталей, не имеющих просветляющих поверхностей, определяется для случая нормального падения из соотношения:
 (1.16)
(1.16)
В общем случае нужно использовать полную формулу Френеля
 (1.17)
(1.17)
где
![]() - показатель
преломления стекла,
- показатель
преломления стекла,
![]() -
углы
падения и преломления,
-
углы
падения и преломления,
![]() определяется
из закона преломления
определяется
из закона преломления
![]()
Линзы
конденсора изготовлены из стекла КУ с
![]() = 1.4584, поэтому
= 1.4584, поэтому
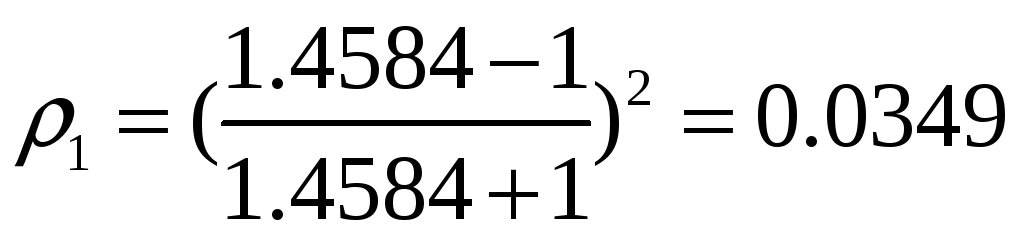
![]()
б) Потерями на поглощение в стекле
![]() (1.18)
(1.18)
где
![]() -
длина
хода луча в средах с коэффициентами
поглощения
-
длина
хода луча в средах с коэффициентами
поглощения
![]()
Коэффициент
поглощения оптических деталей из стекла
КУ равен
![]() =0,002,
длина хода
=0,002,
длина хода
![]() =1,1
см
=1,1
см
![]() 0,99
0,99
