
Высшая математика для 1 и 2 курса
.pdf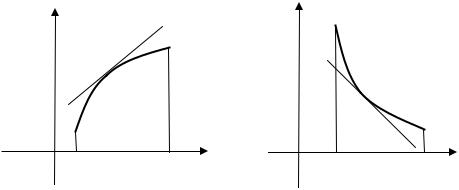
|
|
|
|
|
|
|
|
|
2 |
|
|
− |
2 |
|
+ |
1 |
|
||||||
|
f (x) |
|
x2 − 2x + |
|
|
|
x |
|
1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
k = lim |
= lim |
1 |
= lim |
|
|
|
|
|
|
|
x |
|
|
|
x2 |
|
= 1; |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x→±∞ x |
x→±∞ x(x − 2) |
|
x→±∞ |
|
|
2 |
|
|
− |
2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
b = lim( f (x) - k × x) = lim |
x2 |
- 2x + 1 |
- x = lim |
|
1 |
|
= 0 , |
||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
x→±∞ |
|
x→±∞ |
x - 2 |
|
|
|
|
x→±∞ x - 2 |
|||||||||||||||
то наклонной асимптотой будет прямая y = x .
4.5. Выпуклость и вогнутость графика функции
Определение. График дифференцируемой функции y = f (x) называется выпуклым в интервале (a; b) , если он расположен ниже лю-
бой своей касательной на этом интервале (рис. 4.2 а).
Определение. График дифференцируемой функции y = f (x) называется вогнутым в интервале (a; b) , если он расположен выше любой своей касательной на этом интервале (рис. 4.2 б).
y |
y |
|
O a b x O a b x
a |
б |
|
Рис. 4.2 |
||
|
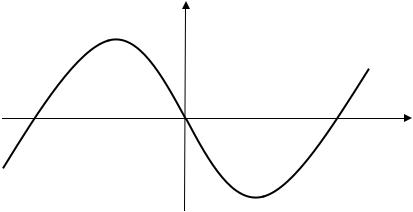
График функции в одних интервалах может быть выпуклым, в других – вогнутым. Например, график функции y = sin x , рассматри-
ваемый в интервале от 0 до 2π , выпуклый в интервале (0; π) и вогнутый в интервале (π; 2π) .
Рассмотрим теперь достаточный признак, позволяющий установить, является ли график функции в данном интервале выпуклым или вогнутым.
61
Теорема. Пусть функция y = f (x) имеет вторую производную f ′′(x) во всех точках интервала (a; b) . Если во всех точках этого интервала f ′′(x) < 0 , то график функции в этом интервале выпуклый, если же f ′′(x) > 0 – вогнутый.
Точка графика непрерывной функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба. В этих точках изменяется направление вогнутости графика функции.
В точке перегиба M 0 (x0 ; y0 ) вторая производная f ′′(x0 ) равна нулю или не существует.
Задача 4. Исследовать на выпуклость и вогнутость функцию f (x) = x3 − 3x .
Решение. |
Находим |
вторую |
производную: |
f ′(x) = 3x2 − 3, |
||
f ′′(x) = 6x . Приравниваем |
f ′′(x) к нулю: |
6x = 0 , откуда x = 0 . Видим, |
||||
что если |
x < 0 , |
то f ′′(x) = 6x < 0 , а если |
x > 0 , то |
f ′′(x) = 6x > 0 , за- |
||
ключаем, что в интервале (−∞,0 ) |
график выпуклый, а в интервале |
|||||
(0, + ∞ ) – |
вогнутый. При x = 0 |
функция имеет |
точку перегиба |
|||
(рис. 4.3). |
|
|
|
|
|
|
y
O |
x |
Рис. 4.3
4.6. Общая схема исследования функции и построения графика
При исследовании функций и построении их графиков полезно придерживаться следующей схемы:
62
1) найти область определения функции и интервалы непрерывно-
сти;
2)если есть точки разрыва, найти односторонние пределы функции в этих точках и изобразить на чертеже поведение функции в каждой точке разрыва;
3)исследовать функцию на четность и нечетность, периодич-
ность;
4)найти вертикальные, горизонтальные и наклонные асимптоты, если они есть;
5)найти интервалы монотонности функции и точки экстремума;
6)найти интервалы выпуклости и вогнутости графика функции, точки перегиба;
7)найти точки пересечения графика функции с координатными осями (если это возможно) и построить график, с учетом полученных результатов.
Задача 5. Исследовать функцию |
y = |
x2 |
и построить ее график. |
|
x2 −1 |
|
|||
Решение
1)Функция не определена при x1 = −1 и x2 = 1, поэтому область определения функции D(y) = (− ∞, − 1) U (− 1, 1) U (1, + ∞).
2)Т. к. в точках x1 = 1 и x2 = −1 функция не определена, то это
точки разрыва функции. Исследуем поведение функции в окрестности этих точек. Для этого вычислим односторонние пределы:
y(1 + 0) = lim |
x2 |
|
= lim |
x2 |
|
= |
|
1 |
|
|
= |
1 |
|
|
= +∞ . |
|
|
− 1 |
(x + 1)(x − 1) |
|
+ 0 |
− 1) |
2(+ |
0) |
|||||||||
x→1+0 x2 |
x→ 1+0 |
2(1 |
|
|
||||||||||||
Вычисленный односторонний предел оказался бесконечным, поэтому прямая x = 1 будет вертикальной асимптотой графика функции.
y(1 − 0) = lim |
x2 |
|
= |
|
1 |
|
|
= |
1 |
|
|
= −∞. |
(x + 1)(x − 1) |
|
− 0 |
− 1) |
2(− |
0) |
|||||||
x→1−0 |
2(1 |
|
|
|||||||||
Вычислим односторонние пределы функции в точке x2 = −1:
y(−1 + 0) = lim |
x2 |
|
= |
1 |
|
= |
1 |
|
= −∞ ; |
|
(x + 1)(x − 1) |
− 2(− 1 + 0 + 1) |
− 2(+ 0) |
||||||||
x→−1+0 |
|
|
|
|||||||
63

y(-1 - 0) = lim |
x2 |
|
= |
1 |
= |
1 |
= +¥ . |
|
(x + 1) (x -1) |
- 2(-1 - 0 + 1) |
- 2(- 0) |
||||||
x→−1−0 |
|
|
|
|||||
Односторонние пределы и в точке x = −1 оказались бесконечными, поэтому прямая x = −1 будет вертикальной асимптотой графика функции.
3) Поскольку y(- x) = |
(- x)2 |
= |
x2 |
|
= y(x), то функция четная. |
|
|
||||
|
(- x)2 -1 x2 -1 |
|
|||
4) Т. к. односторонние пределы функции в точках x1 = −1 и x2 = 1, то прямые x1 = −1 и x2 = 1 будут вертикальными асимптотами графика
функции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = k x + b |
|
|
|||||||
Для нахождения наклонной асимптоты (4.1) |
|
|
|
графика |
|||||||||||||||||||||||||||||||||||||||||
функции |
вычислим |
|
два |
|
предела (4.3): |
|
|
|
|
|
k = lim |
f (x) |
и |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
b = lim ( f (x) − k x): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→ ∞ |
x |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
¥ |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||
|
k = lim |
|
|
|
|
|
|
|
|
|
= |
|
|
= lim |
|
|
|
|
|
|
|
= |
|
|
|
|
= 0 ; |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
x→∞ x(x2 -1) |
|
¥ |
|
|
|
|
x→∞ x(1 - |
) |
|
|
¥ |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
|
|
|
- 0 |
= lim |
|
2 |
|
|
= lim |
|
|
|
1 = |
|
|
|
|
=1. |
|
|||||||||||||||||||||
b = lim |
|
|
|
|
|
× x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
x→ ∞ x |
|
|
- |
1 |
|
|
|
|
x→∞ x |
|
|
-1 |
|
x→∞ 1 |
- |
|
|
|
|
1 - |
0 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
x2 |
|
|
|
||||||||||||||||||||||||||||||||||
Значит, |
прямая |
|
|
y = 0 × x + 1, |
|
т. |
|
е. |
y = 1 |
|
– |
|
|
это |
|
|
горизонтальная |
||||||||||||||||||||||||||||
асимптота графика функции и при х®+¥, и при х® – |
|
|
¥. |
|
|
|
|||||||||||||||||||||||||||||||||||||||
5) Вычислим |
производную, найдем критические точки, |
интерва- |
|||||||||||||||||||||||||||||||||||||||||||
лы монотонности и точки экстремума: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
x |
2 |
|
|
|
= 2x(x |
2 |
-1)- x |
2 |
× 2x = - 2x |
|
; |
|
|
|
||||||||||||||||||||||||||||
|
y¢ = |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
(x2 -1)2 |
|
|
|
|
|
|
(x2 -1)2 |
|
|
|
|
|
|||||||||||||||||||||||
|
|
x2 -1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
y¢ = |
− 2x |
|
= 0, x = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
(x2 -1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
В точках x1 = −1 и x2 = 1 производная не существует.
64
Составим таблицу изменений знака производной y′ (табл. 4.1).
Таблица 4.1
|
x |
(– ∞; –1) |
|
–1 |
(–1; 0) |
|
0 |
|
(0; 1) |
|
1 |
(1; + ∞) |
|
y′ |
+ |
|
не сущ. |
+ |
|
0 |
|
– |
|
не сущ. |
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
возр. |
|
экстр. |
возр. |
|
макс. |
убыв. |
|
экстр. |
убыв. |
|
|
|
нет |
|
ymin |
= 0 |
|
нет |
|||||
|
|
|
|
|
|
|
|
|
||||
|
Т. к. y′ > 0 при x (− ∞; − 1) U (− 1;0), то на этих интервалах функ- |
|||||||||||
ция возрастает. |
При x (0; 1) U (1; + ∞) |
производная |
y′ < 0 , следова- |
|||||||||
тельно, на этих интервалах функция убывает. |
|
|
|
|
||||||||
|
Поскольку |
′ |
|
= 0 – единственная критическая точка |
||||||||
|
y (0) = 0 , то x |
|||||||||||
функции, а т. к. y′ меняет знак в точке 0 с «+» на «–», |
то x = 0 – точ- |
|||||||||||
ка максимума функции, причем y(0) = 0 . |
|
|
|
|
||||||||
y
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
− 2 −1 |
|
0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
− 4 |
− 3 |
1 |
2 |
3 |
4 |
x |
||||||||||
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
− 2 |
|
|
|
|
||||||
Рис. 4.4
6) Интервалы выпуклости и вогнутости найдем по знаку производной второго порядка y′′ . Найдем вторую производную и возмож-
ные точки перегиба:
|
- 2x |
′ |
|
1× (x2 -1)2 - x × 2(x2 -1)2x |
|
2(1 + 3x2 ) |
|||
y¢¢ = |
|
|
= -2 |
|
|
= |
|
|
. |
2 |
4 |
(x2 |
3 |
||||||
|
(x2 -1) |
|
|
|
(x2 -1) |
|
-1) |
|
|
65
В точках x1 = −1 и x2 = 1 вторая производная не существует. Составим таблицу изменений знака y′′ (табл. 4.2).
|
|
|
|
|
|
Таблица 4.2 |
х |
(– ¥; –1) |
–1 |
|
(–1; 1) |
1 |
(1; + ¥) |
y′′ |
+ |
не сущ. |
|
– |
не сущ. |
+ |
у |
È (вогн.) |
не сущ. |
|
Ç (выпукл.) |
не сущ. |
È (вогн.) |
Итак, на интервалах (– ∞; –1) |
и (1; +∞) график функции вогнутый, |
|||||
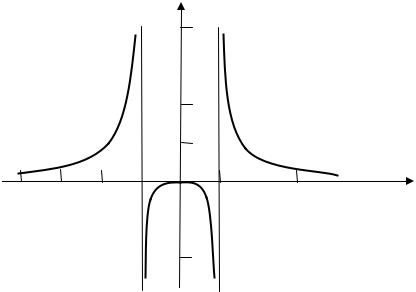
ана интервале (–1; 1) – выпуклый. Точек перегиба нет.
7)Учитывая, что y(0) = 0, строим график (рис. 4.4).
Задача 6. Исследовать функцию y = xe− x и построить ее график.
Решение
1)Область определения функции – вся числовая прямая, т. е.
D( y) = R .
2)Данная функция является элементарной функцией, определенной на всей числовой оси, значит, точек разрыва, а следовательно и вертикальных асимптот нет.
3)Т. к. y(- x) ¹ y(x) и y(- x) ¹ -y(x), то y(x) – ни четная, ни
нечетная функция.
4) Исследуем наличие наклонной асимптоты при x → +∞ . Т. к.
k = lim |
f (x) |
= lim |
xe− x |
= lim |
1 |
= |
1 |
= 0 : |
|||||
|
|
|
|
|
|
||||||||
x |
→ + ∞ x |
x |
→ + ∞ x |
x |
→ + ∞ e |
x |
|
|
|
||||
|
|
|
|
|
+ ∞ |
|
|||||||
b = lim ( f (x) − k x) = lim |
x |
= ∞ |
= lim |
x′ |
= lim |
1 |
= |
1 |
|
= 0 , |
||||
|
(e x )′ |
|
|
|
||||||||||
|
|
e |
x |
∞ |
|
|
e |
x |
+ ∞ |
|
||||
x→+ ∞ |
x→+ ∞ |
|
|
x→+ ∞ |
|
x→+ ∞ |
|
|
|
|
||||
|
|
|
|
|
|
|||||||||
то прямая у = 0 – горизонтальная асимптота графика функции при
x → +∞ (являющаяся |
частным |
случаем |
наклонной асимптоты при |
|||||
x → +∞ ). |
|
|
|
|
|
|
|
|
Исследуем наличие наклонной асимптоты при x → −∞ . Т. к. |
||||||||
k = lim |
f (x) |
= lim |
xe− x |
= lim |
1 |
= e+∞ = +∞ , |
||
|
|
|
|
|
||||
|
x |
x |
|
|||||
x→ − ∞ |
x→ − ∞ |
x→ − ∞ e x |
|
|||||
то при x → −∞ наклонной асимптоты нет.
66

5) Вычислим производную, найдем критические точки, интервалы монотонности и точки экстремума:
y¢ = (xe−x )′ =1×e−x - x ×e−x = (1- x)e−x : y′ = (1 − x)e− x = 0 x = 1.
Составим таблицу изменений знака производной y′ (табл. 4.3).
|
|
|
|
|
|
|
|
Таблица 4.3 |
x |
|
(– ∞; –1) |
|
|
|
1 |
|
(1; +∞) |
y′ |
|
+ |
|
|
|
0 |
|
– |
|
|
|
|
|
|
|
||
|
|
|
|
максимум |
|
|
||
y |
|
возрастает |
|
y |
|
= e−1 |
|
убывает |
|
|
|
|
max |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Т. к. |
y′ > 0 при x < 1 и y′ < 0 при x > 1, то функция при x < 1 |
|||||||
возрастает, а при x > 1 убывает. Т. к. |
y′(1) = 0 , то x = 1 – |
единственная |
||||||
критическая точка функции. Поскольку в критической точке функция меняет знак с «+» на «–», то x = 1 – точка максимума функции и
y(1) = e−1 = 1 . e
6) Интервалы выпуклости и вогнутости найдем по знаку производной второго порядка y′′ . Найдем вторую производную и возмож-
ные точки перегиба:
y′′ = ((1− x) e−x )′ = −e−x − (1− x) e−x = (x − 2) e−x ; y′′ = (x − 2) = 0 x = 2 .
Составим таблицу изменений знака y′′ (табл. 4.4).
|
|
|
|
|
|
Таблица 4.4 |
|
х |
(– ¥; 2) |
|
2 |
|
(2; + ¥) |
|
y′′ |
– |
|
0 |
|
+ |
|
у |
Ç (выпукл.) |
|
2 × e−2 |
|
È (вогн.) |
|
Т. к. y′′ > 0 при x > 2 и y′′ < 0 при x < 2 , то при x > 2 график |
|||||
функции вогнутый, а при x < 0 – |
выпуклый. |
Т. к. в точке x = 2 y′′ |
||||
меняет знак, то точка M (2; 2a−2 ) – |
точка перегиба графика функции. |
|||||
67
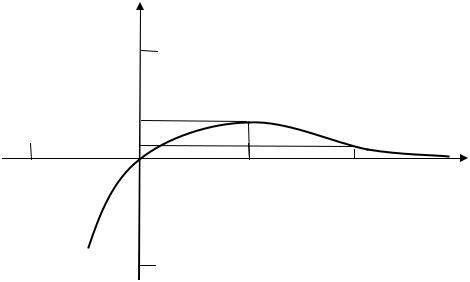
7) Учитывая, что y(0) = 0 , строим график функции (рис. 4.5).
y
e−1 |
M |
|
e−2 |
||
|
− 0 2 x
−
Рис. 4.5
68
Тема 5. Неопределенный интеграл
5.1. Первообразная и неопределенный интеграл
Определение. Функция F (x) называется первообразной для за-
′ |
|
данной функции f (x), если F (x) = f (x). |
|
Определение. Множество всех первообразных для функции f (x) |
|
называется неопределенным интегралом от функции |
f (x) и обозна- |
чается ∫ f (x)dx . |
|
Итак, если F ′(x) = f (x) , то |
|
∫ f (x) dx = F(x) + C . |
(5.1) |
При вычислении неопределенных интегралов используют свойства интегралов, таблицу неопределенных интегралов, различные методы интегрирования, а также тождественные преобразования подынтегральной функции.
Свойства неопределенных интегралов.
1.∫ dF (x) = F (x) + C.
2.∫( f ( x) ± g ( x)) dx = ∫ f ( x) dx ± ∫ g ( x) dx.
3. |
∫ kf (x)dx = k ∫ f (x)dx, где k = const. |
||
4. |
∫ f (ax + b)dx = |
1 |
F (ax + b) + C . |
|
|||
|
|
a |
|
Таблица неопределенных интегралов.
α+1
1. ∫ xα dx = αx + 1 + C, (n ¹ -1).
2. ∫ dxx = ln x + C. 3. ∫ ex dx = ex + C.
4. ∫ a x dx = a x + C. lna
69

5.∫sin xdx = −cos x + C.
6.∫ cos xdx = sin x + C.
7. ∫ |
|
|
|
|
dx |
|
|
= tgx + C. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
cos |
2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
8. ∫ |
|
|
|
|
dx |
|
|
= −ctgx + C. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
sin |
2 |
x |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
9. ∫ |
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
= arcsin |
|
x |
|
+ C. |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
a |
2 |
− x |
2 |
a |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
10 ∫ |
|
|
|
|
|
dx |
|
|
|
= |
1 |
arctg |
x |
+ C. |
|
|
|
|
|||||||||||||||||||
a |
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
+ x |
|
|
|
|
|
|
a |
|
|
a |
|
|
|
|
|
|
|
|
|
|||||||||||||
11. ∫ |
|
|
|
dx |
|
|
|
|
|
= |
|
1 |
|
|
|
x − a |
|
+ C. |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ln |
|
|
|
|
|||||||||||||||||||||||
x |
2 |
|
|
2 |
|
|
|
x + a |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
− a |
|
|
|
|
|
|
|
2a |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
12. ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ln |
|
x + |
|
|
x 2 ± a 2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
x 2 |
± a 2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Задача |
|
1. Вычислить ∫ 4x3 |
- |
||||||||||||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||||
+ C.
|
|
2 |
|
|
|
1 |
|
|
|
+ |
|
|
- |
|
|
|
|
||
|
|
|
|
|
|
|
|||
|
+ x |
2 |
|
25 + x |
2 |
|
dx . |
||
9 |
|
|
|
|
|
|
|||
Решение. Используя свойства и таблицу неопределенных интегралов, получим:
|
|
3 |
|
1 |
|
2 |
|
|
|
1 |
|
|
|
|
4x |
- |
+ |
|
- |
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||
∫ |
|
x |
2 |
9 + x |
2 |
|
25 + x |
2 |
dx = |
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
= 4∫ x3 dx −∫ x−2 dx +2∫ |
|
dx |
|
− ∫ |
|
|
dx |
|
|
|
|
= |
|||||||||||||||||||||
|
|
2 |
+ x |
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
3 |
5 |
2 |
+ x |
2 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
x3+1 |
|
- 2 + 1 |
|
2 |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= 4 × |
|
- |
+ |
arctg |
|
|
- ln |
x + |
25 + x |
2 |
|
|
+ C = |
|||||||||||||||||||||
|
|
|
|
x−2+1 |
|
|
|
|
|
|
|
|||||||||||||||||||||||
3 + 1 |
3 |
3 |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
= x4 |
+ |
1 |
+ |
2 |
|
x |
− ln |
|
x + |
|
|
|
|
+ C . |
||||||||||||||||||
|
|
arctg |
|
|
25 + x2 |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
70
