
Механика материалов для з.о._Дорожко.2010
.pdf
|
|
|
|
|
|
|
|
|
|
|
Таблица 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Номер |
|
Схема по |
Уголок равнобокий b×b×δ |
|
|
|
|
|
|
||
|
|
|
№ швеллера |
№ двутавра |
||||||||
|
|
|
|
|
|
|
|
|
||||
|
строки |
|
рис. 4 |
b, мм |
|
δ, мм |
|
|
|
|
|
|
|
|
10 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
1 |
40 |
|
4 |
|
10 |
|
||||
2 |
|
2 |
50 |
|
3 |
12 |
|
12 |
|
|||
3 |
|
3 |
70 |
|
6 |
14 |
|
14 |
|
|||
4 |
|
4 |
80 |
|
7 |
|
14а |
16 |
|
|||
5 |
|
5 |
90 |
|
9 |
16 |
|
18 |
|
|||
6 |
|
6 |
100 |
|
12 |
|
16а |
|
18а |
|||
7 |
|
7 |
110 |
|
8 |
18 |
|
20 |
|
|||
8 |
|
8 |
125 |
|
10 |
|
18а |
|
20а |
|||
9 |
|
9 |
125 |
|
16 |
20 |
|
22 |
|
|||
0 |
|
10 |
140 |
|
12 |
|
20а |
|
22а |
|||
|
|
|
а |
|
б |
|
|
в |
|
а |
||
Задача 5. Перемещения при изгибе
На рис. 5 показана консольная балка, имеющая постоянную жесткость EI.
Требуется:
1)записатьвобщем виде(вдолях1 / EI) прогиббалкивточкахВиС;
2)построить эпюру прогибов балки в долях 1 / EI по трем точкам
всечениях А, В и С.
Данные взять из табл. 6.
Таблица 6
Номер |
Схема |
a, м |
b, м |
q, |
F1, кН |
F2, кН |
M1, |
M2, |
строки |
по рис. 5 |
|
|
кН/м |
|
|
кНм |
кНм |
1 |
1 |
1,1 |
1,1 |
11 |
– |
11 |
11 |
– |
2 |
2 |
1,2 |
1,2 |
12 |
12 |
– |
– |
12 |
3 |
3 |
1,3 |
1,3 |
13 |
– |
13 |
13 |
– |
4 |
4 |
1,4 |
1,4 |
4 |
4 |
– |
– |
4 |
5 |
5 |
1,5 |
1,5 |
5 |
– |
5 |
15 |
– |
6 |
6 |
1,6 |
1,6 |
6 |
6 |
– |
– |
6 |
7 |
7 |
1,7 |
1,7 |
7 |
– |
7 |
7 |
– |
8 |
8 |
1,8 |
1,8 |
8 |
8 |
– |
– |
8 |
9 |
9 |
1,9 |
1,9 |
9 |
– |
9 |
9 |
– |
0 |
10 |
2,0 |
2,0 |
10 |
10 |
– |
– |
10 |
|
а |
б |
в |
г |
б |
б |
в |
в |
21
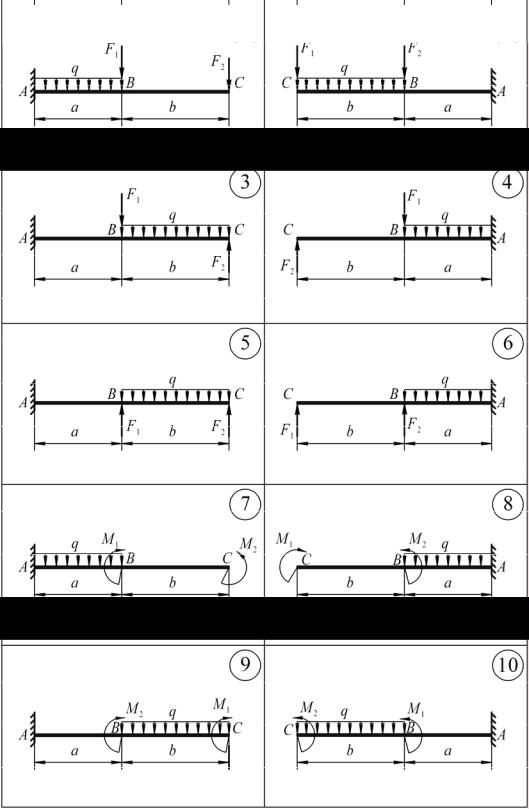
Рис. 5. Расчетные схемы к задачам 5 и 6 (перемещения при изгибе. Косой изгиб)
22
Указание: для расчета прогиба предпочтительно использовать метод начальных параметров, т. к. угол поворота сечения и прогиб балки в заделке известен.
Задача 6. Косой изгиб
Консольная балка прямоугольного поперечного сечения с продольной осью х нагружена в двух плоскостях.
Нагрузки, действующие на балку в вертикальной плоскости xy, показаны на рис. 5.
В горизонтальной плоскости xz на балку действует сила F1, приложенная в точке В, или сила F2, приложенная в точке С (в зависимости от варианта). Направление этих сил совпадает с направлением оси z.
Плоскость действия всех нагрузок совпадает с осями симметрии z, y прямоугольного поперечного сечения балки.
Требуется: из условия прочности подобрать сечение балки, если соотношение сторон прямоугольника α = h / b . Данные взять из табл. 7.
Таблица 7
Номер |
Схема по |
a, м |
b, м |
q, |
F1, |
F2, |
M1, |
M2, |
α |
строки |
рис. 5 |
|
|
кН/м |
кН |
кН |
кНм |
кНм |
|
1 |
1 |
1,1 |
1,1 |
11 |
– |
11 |
11 |
– |
2,1 |
2 |
2 |
1,2 |
1,2 |
12 |
12 |
– |
– |
12 |
2,2 |
3 |
3 |
1,3 |
1,3 |
13 |
– |
13 |
13 |
– |
2,3 |
4 |
4 |
1,4 |
1,4 |
4 |
4 |
– |
– |
4 |
2,4 |
5 |
5 |
1,5 |
1,5 |
5 |
– |
5 |
15 |
– |
2,5 |
6 |
6 |
1,6 |
1,6 |
6 |
6 |
– |
– |
6 |
2,6 |
7 |
7 |
1,7 |
1,7 |
7 |
– |
7 |
7 |
– |
2,7 |
8 |
8 |
1,8 |
1,8 |
8 |
8 |
– |
– |
8 |
2,8 |
9 |
9 |
1,9 |
1,9 |
9 |
– |
9 |
9 |
– |
2,9 |
0 |
10 |
2,0 |
2,0 |
10 |
10 |
– |
– |
10 |
3,0 |
|
а |
б |
в |
г |
б |
б |
в |
в |
в |
Указания:
1. На расчетной схеме, размещенной целиком на одной странице (как показано в примере на рис. 6), следует:
а) показать нагрузки, действующие на балку в вертикальной плоскостиxy ипостроитьэпюрыпоперечныхсилQy иизгибающихмоментовMz; б) показать нагрузки, действующие на балку в горизонтальной плоскостиxz, ипостроитьэпюрыпоперечныхсилQz иизгибающихмоментовMy;
23
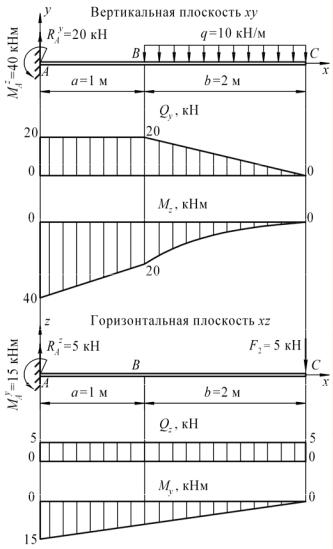
Рис. 6. Пример к задаче 6
в) обозначить сечения с максимальными изгибающими моментами, действующими в вертикальной и в горизонтальной плоскостях.
2.Осевые моменты сопротивления Wy и Wz выразить через один из размеров сечения на основании соотношения α.
3.Положение опасного сечения определить по наибольшему напряжению, действующему в балке. Для его нахождения следует выразить и сравнить максимальные напряжения в сечениях с наибольшими изгибающими моментами, действующими или в одной из плоскостей, или в двух плоскостях одновременно, в зависимости от конфигурации эпюр.
4.Размер сечения вычислить из условия прочности балки при неплоском (косом) изгибе.
24
Задача 7. Внецентренное сжатие
Короткий чугунный стержень, поперечное сечение которого показано на рис. 7, сжимается продольными силами F1 или F2, приложенными в точках В и D соответственно.
Требуется:
1)определить геометрические характеристики поперечного сечения стержня;
2)построить нейтральную линию и определить положение опасных точек;
3)вычислить наибольшие растягивающие и сжимающие напряжения, возникающие в стержне;
4)дать заключение о прочности стержня, если допускаемое на-
пряжение на сжатие [σс] = 100 МПа, допускаемое напряжение на растяжение [σр] = 40 МПа.
Указания:
1.Для решения задачи следует вычертить сечение в масштабе 1:1, обозначить на нем все необходимые для расчета размеры и точки по аналогии с задачей 4;
2.Поскольку все варианты сечений имеют ось симметрии, она будет одной из главных центральных осей инерции, что упрощает расчет геометрических характеристик. В связи с этим достаточно вычислить только одну координату центра тяжести. Кроме того, нет необходимости рассчитывать центробежный момент инерции сечения и направление главных центральных осей инерции (см. п. 6–7 задачи 4).
Данные взять из табл. 8.
|
|
|
|
|
Таблица 8 |
|
|
|
|
|
|
Номер строки |
Схема по |
а, см |
b, см |
F1, кН |
F2, кН |
рис. 6 |
|
||||
|
|
|
|
|
|
1 |
1 |
2,1 |
2,1 |
10 |
– |
2 |
2 |
2,2 |
2,2 |
– |
20 |
3 |
3 |
2,3 |
2,3 |
30 |
– |
4 |
4 |
2,4 |
2,4 |
– |
40 |
5 |
5 |
2,5 |
2,5 |
50 |
– |
6 |
6 |
3,6 |
3,6 |
– |
60 |
7 |
7 |
3,7 |
3,7 |
70 |
– |
8 |
8 |
3,8 |
3,8 |
– |
80 |
9 |
9 |
3,9 |
3,9 |
90 |
– |
0 |
10 |
4,0 |
4,0 |
– |
100 |
|
а |
б |
в |
б |
б |
25
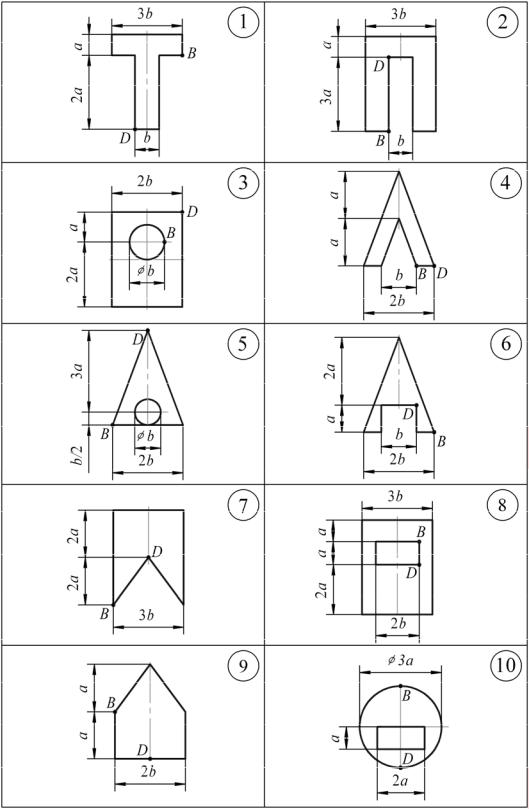
Рис. 7. Расчетные схемы к задаче 7 (внецентренное сжатие)
26

Задача 8. Совместное действие изгиба и кручения
На трансмиссионном валу закреплен шкив ременной передачи и зубчатое колесо (рис. 8а, 8б). Вал передает мощность N, кВт, при частоте вращения ω, с–1.
В ременной передаче ветви ремня параллельны. Его ведущая ветвь натянута в η раз больше ведомой. Положение ветвей определяется углом α.
Усилие, действующее в зубчатом зацеплении, разложено на окружную Ft и радиальную составляющие Fr. Между собой они связаны соотношением: Fr = 0,4 Ft. Направление окружного усилия Ft задано углом β.
Требуется:
1)определить крутящие моменты, приложенные к шкиву и зубчатому колесу по заданным N и ω;
2)составить расчетную схему вала для расчета на кручение и построить эпюру крутящих моментов Мк;
3)определить окружные усилия в передачах через передаваемый ими крутящий момент (для ременной передачи с учетом разности натяжения ветвей).
Радиальное усилие Fr в зубчатой передаче вычисляется через соотношение с окружным Ft;
4)определить вертикальные Vi и горизонтальные усилия Hi, действующие на вал в местах установки шкива и зубчатого колеса;
5)составить расчетные схемы вала в двух плоскостях: вертикальной V горизонтальной H.
Для этого вал представляют в виде балки на двух опорах. Затем
поочередно нагружают его вертикальными Vi и горизонтальными Hi усилиями;
6)построить эпюры изгибающих моментов от вертикальных сил МV и от горизонтальных сил МH;
7) построить эпюру суммарного изгибающего момента
Mc =  MV2 + M H2 ;
MV2 + M H2 ;
8)из анализа эпюр Мк и Мс определить положение опасного сечения и вычислить наибольший эквивалентный момент Мэкв, используя для этого энергетическую (четвертую) теорию прочности;
9)подобрать диаметр вала d при [σ] = 100 МПа и округлить его значение (см. задачу 2).
27
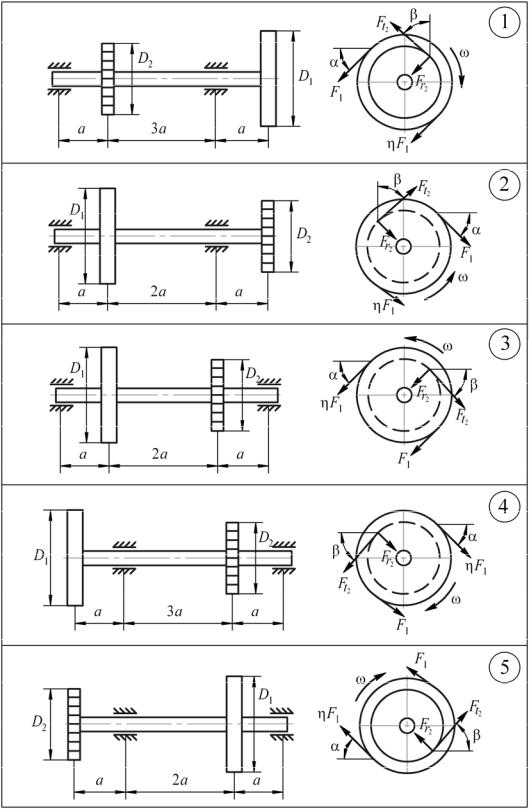
Рис. 8а. Расчетные схемы 1–5 к задаче 8 (совместное действие изгиба и кручения)
28
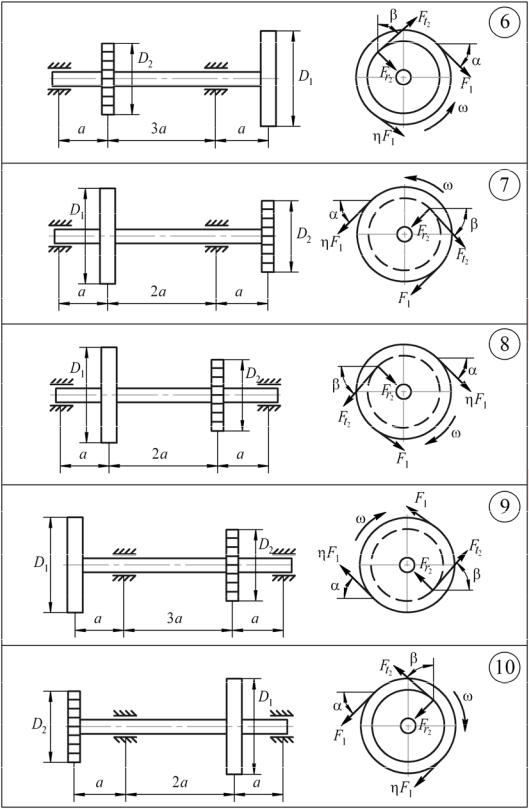
Рис. 8б. Расчетные схемы 6–10 к задаче 8 (совместное действие изгиба и кручения)
29

Данные для решения этих задач взять из табл. 9.
|
|
|
|
|
|
|
|
|
Таблица 9 |
|
|
|
|
|
|
|
|
|
|
|
|
Номер |
Схема |
a, м |
D1, м |
D2, м |
ω, с–1 |
α, ° |
β, ° |
η |
|
N, |
строки |
по рис. 7 |
|
|
|
|
|
|
|
|
кВт |
1 |
1 |
0,21 |
0,31 |
0,21 |
25 |
0 |
45 |
2,1 |
|
21 |
2 |
2 |
0,22 |
0,32 |
0,22 |
30 |
30 |
60 |
2,2 |
|
22 |
3 |
3 |
0,23 |
0,33 |
0,23 |
35 |
45 |
90 |
2,3 |
|
33 |
4 |
4 |
0,24 |
0,34 |
0,24 |
40 |
60 |
0 |
2,4 |
|
44 |
5 |
5 |
0,25 |
0,35 |
0,25 |
45 |
90 |
30 |
2,5 |
|
55 |
6 |
6 |
0,26 |
0,46 |
0,26 |
50 |
0 |
45 |
2,6 |
|
16 |
7 |
7 |
0,27 |
0,47 |
0,27 |
55 |
30 |
60 |
2,7 |
|
27 |
8 |
8 |
0,28 |
0,48 |
0,28 |
60 |
45 |
90 |
2,8 |
|
28 |
9 |
9 |
0,29 |
0,49 |
0,29 |
65 |
60 |
0 |
2,9 |
|
39 |
0 |
10 |
0,30 |
0,50 |
0,30 |
70 |
90 |
30 |
3,0 |
|
40 |
|
а |
б |
в |
г |
а |
б |
в |
г |
|
а |
Задача 9. Устойчивость сжатых стержней
Стержень с известными размерами, изготовленный из стали Ст. 3, сжимается силой F (рис. 9). Схема закрепления стержня показана на левой стороне рис. 9, а поперечное сечение на правой.
Требуется:
1) рассчитать допускаемое значение силы Fдоп, если [σ] =
=160 МПа;
2)определить коэффициент запаса устойчивости n. Данные взять из табл. 10.
|
|
|
Таблица 10 |
|
|
|
|
l, м |
|
Номер строки |
Схема по рис. 8а, 8б |
а, см |
|
|
1 |
1 |
2,1 |
1,1 |
|
2 |
2 |
2,2 |
1,2 |
|
3 |
3 |
2,3 |
1,3 |
|
4 |
4 |
2,4 |
1,4 |
|
5 |
5 |
5,4 |
1,5 |
|
6 |
6 |
2,6 |
1,6 |
|
7 |
7 |
2,7 |
1,7 |
|
8 |
8 |
2,8 |
1,8 |
|
9 |
9 |
2,9 |
1,9 |
|
0 |
10 |
3,0 |
2,0 |
|
|
а |
б |
в |
|
30
