54. Признаки сходимости рядов с положительными членами. Признаки сравнения.

Признак сравнения 1.

Пусть даны два ряда с положительными членами ,, причем каждый член рядане превосходит соответствующего члена ряда..

Тогда если сходится ряд , то сходится и ряд; если расходится ряд, то расходится и ряд.

Признак сравнения 2, или признак сравнения в предельной форме.

Пусть даны два ряда с положительными членами ии пусть существует конечный и не равный нулю. Тогда оба ряда сходятся или расходятся одновременно.

55. Признаки сходимости рядов с положительными членами. Признак Даламбера

Признак Даламбера. Если для положительного ряда существует конечный предел

 ^,

то этот ряд сходится при L<1 и расходится при L>1.

56. Признаки сходимости рядов с положительными членами. Интегральный признак Коши. Степенной признак сравнения

Интегральный признак. Если при– непрерывная, положительная и монотонно убывающая функция, то ряд, где, сходится или расходится в зависимости от того, сходится или расходится интеграл

57.Знакочередующиеся ряды. Признак Лейбница.

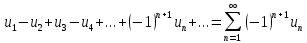
Где , для всехn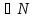 (т.е. ряд, положительные и отрицательные члены которого следуют друг за другом поочередно)

Признак Лейбница

Если для рядавыполняются условия:то этот ряд сходится, причем его сумма удовлетворяет неравенствам

58. Общий достаточный признак сходимости знакопеременных рядов. Абсолютная и условная сходимости числовых рядов. Свойства абсолютно сходящихся рядов.

 Пусть дан знакопеременный ряд

.

Если сходится ряд

,

составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд.

Абсолютная и условная сходимость

Ряд называетсяабсолютно сходящимся, если ряд также сходится.  Если рядсходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение неверно.  Рядназываетсяусловно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.

Свойства:

1. Если ряд абсолютно сходится и имеет сумму S, то ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму S, что и исходный ряд.(теорема Дирихле)

2. Абсолютно сходящиеся ряды с суммами 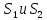, можно пчленно складывать(вычитать). В результате получается абсолютно сходящийся ряд, сумма которого равна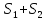,(или соотв-о,)

3. Под произведением двух рядов 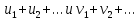понимают ряд вида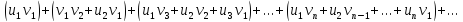

Произведение двух абсолютно сходящихся рядов с суммами есть абсолютно сходящийся ряд, сумма кот.равна

59. Функциональные ряды. Основные понятия

Ряд , члены которого являются функциями от переменной, называется функциональным.

При различных значениях из функционального ряда получаются различные числовые ряды, которые могут быть сходящимися или расходящимися.

Если ряд сходится то -наз. точкой сходимости

Если расходится то -наз. Точкой расходимости.

Совокупность числовых значений аргумента , при которых функциональный ряд сходится, наз. Его областью сходимости.

Очевидно, что в области сходимости функционального ряда его сумма является функцией от . Будем ее обозначать.