12. Интегралы с переменным верхним пределом.

Работа переменной силы F, величина которой есть непрерывная ф-я F=F(x), действующей на отрезке [a;b], равна определённому интегралу от величины F(x) силы, взятому по отрезку [a;b].

13. Формула Ньютона-Лейбница.

Если ф-я y=f(x) непрерывна на отрезке [a;b] и F(x) —какая-либо её первообразная на [a;b] (F^’(x)=f(x)), то имеет место формула

13. Замена переменной в ОИ.

Если: 1) ф-я x=φ(t) и её производная x^’=φ^’(t) непрерывна при t Є [α;β];

2) множеством значений ф-ии x=φ(t) при t Є [α;β] является отрезок [a;b];

3) φ(α)=α и φ(β)=b,то

13. Интегрир. по частям в ОИ.

Если ф-ии u=u(x) и v=v(x) имеют непрерывные производные на отрезке [a;b], то имеет место формула:

13. Несобст. интегралы по бесконечному промежутку.

несобственный инт.1-го рода:

если указанного предела не существует или он бесконечен, то говорят, что он расходится.

несобственный инт. с 2-мя бесконечными пределами определяются формулой:

13. Несобственные интегралы от неограниченных ф-ций. Примеры

Пусть функция f(x) определена на полуинтервале (a, b], интегрируема по любому отрезку , и имеет бесконечный предел при

. Несобственным интегралом от f(x) по отрезку [a, b] называется предел

. Если этот предел конечен, говорят, что интеграл сходится; если предел не существует или бесконечен, говорят, что интеграл расходится.

18. Вычисление площадей в декартовой.

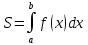или

18. Вычисление площадей в полярной системе.

18. Длина дуги кривой.

Длина дуги AB – предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наиб. звена её стремится к нулю.

18. Вычисление V тел по S поперечных сечений.

18. Вычисление V тел вращений.

18. Вычисление S пов. вращения.

18. Диф. уравнения 1-го порядка.

Это уравнения вида: F(x;y;y^’)=0

Если уравнение можно записать относительно , то его записывают:

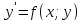
Если в этом уравнении ф-я f(x;y) и её частная производная непрерывны в некоторой обл.D, содержащей т. (x₀;y_0­­), то сущ. единственное решение y=φ(x) этого уравнения, удовлетворяющее начальному условию.

Геометрический смысл теоремы состоит в том, что при выполнении её условий существует единственная интегральная кривая ДУ, проходящая через т. (x₀;y_0­­)

18. Диф. уравн. с раздел. переем.

Наиб. простым ДУ является уравн. вида:

P(x)∙dx+Q(y)∙dy=0

его общий интеграл:

18. Линейные диф. уравнения.

Уравнение наз. линейным, если его можно записать в виде: y^’+p(x)∙y=g(x)

Для их решения используются 2 метода: Бернулли и Лагранжа.

18. Диф. уравн., допускающие понижение степени.

Одним из методов интегрирования ДУ высших порядков является метод понижения порядка. Суть метода состоит в том, что с помощью замены переменной( подстановки) данное ДУ сводится к уравнению, порядок которого ниже.

1 тип: y^’’=f(x)

2 тип: y^’’=f(x;y^’)

3 тип: y^’’=f(y;y^’)

18. Диф. уравнения 2-го порядка.

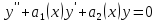
Если ф-ии y₁=y₁(x) и y₂=y₂(x) являются частными решениями уравнения, то решением этого уравнения является также ф-я

y=c₁y₁(x)+c₂y₂(x)

Если диф-мые ф-ии y_1­(x) и y₂(x) линейно зависимы на (a;b), то определитель Вронского на этом интервале тождественно = 0

Если ф-ии y_1­(x) и y₂(x) – линейно независимые решения уравнения на (a;b), то определитель Вронского на этом интервале никогда не обращается в нуль.

Если 2 частных решения y₁=y₁(x) и y₂=y₂(x) ЛОДУ образуют на интервале (a;b) фундаментальную систему, то общим решением этого уравнения является ф-я y=c₁y₁+c₂y_2.

18. Линейные диф-е уравн. n-го порядка.

Частным случаем линейных однородных диф-ых уравн. являются ЛОДУ с постоянными коэф.

Пусть дано ЛОДУ 2-го порядка: y^’’+p∙y^’+q∙y=0

Для нахождения общего решения уравнения достаточно найти 2 его частных решения, образующих фундаментальную систему.

Будем искать частные решения уравнения в виде y=e^kx. Диф-уя эту ф-ю 2 раза и подставляя выражения для ,в уравнеия, получим:k²∙e^kx+p∙k∙e^kx+q∙e^kx=0

Получившееся ураснение наз. характеристическим ДУ.

18. Неоднородные линейные диф. уравнения 2-го порядка.

Общим решением y уравнения является сумма его произвольного частного решения y^* и общего решения ŷ=c₁y₁+c₂y₂ соответствующего однородного уравнения

y=y^*+ ŷ

18. Метод Лагранжа…

y=y^*+ ŷ

Частное решение y^*уравнения можно найти, если известно общее решение ŷ соответствующего однородного уравнения, методом вариации произвольных постоянных.

18. Система линейных диф. уравнений…

Системой ДУ наз. совокупность ДУ, каждое из которых содержит независимую переменную, искомые ф-ии и их производные. Решением системы наз. совокупность из n ф-ий y₁, y₂,…, y_n, удовлетворяющих каждому из уравнений этой системы.

Если в системе все ф-ии

f_i(x; y₁; …, y_n) непрерывны вместе со всеми своими частными производными по y_i в некот. обл. D ((n+1)-мерного пространства), то в каждой т. M₀(этой области сущ., и при том единственное, решениеy₁=φ₁(x), y₂=φ₂(x), …, y_n=φ_n(x) системы, удовлетворяющее начальным условиям.