45.Приложение кри-1 рода

Длина кривой:

Площадь цилиндрической поверхности:

Масса кривой:

Статические моменты:

46.Условия независимости кри-2 от пути интегрирования. Потенциал

Для того чтобы криволинейныйинт. не зависел от пути интегрирования в односвязной областиD, в которой функции непрерывны вместе со своими частными производными, необходимо и достаточно, чтобы в каждой точке этой области выполнялось условие:

47. Приложения кри II рода

Площадь плоской фигуры: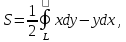

При этом кривая L обходится против часовой стрелки:

48. Основные понятия теории поля. Потенциальные векторные поля. Циркуляция

Полем называется область V пространства, в каждой точке которой определено значение некоторой величины. Если каждой точке М этой области соотв. Опред. Число U=U(M). Говорят, что в области определено (задано) скалярное поле(или функция точки).Если же каждой точке каждой точке М области пространства соотв. Некоторый вектор то говорят, что задано векторное поле(или векторная функция точки).если скалярное поле не зависит от времени- стационарное. Если меняется с течение времени –нестационарное.

Вектор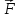определяющий векторно поле, можно рассм. как векторную функцию трех скалярных аргументовx,y,z:

Векторной линией поля наз. Линия, касательная к кот.в точке в каждой точке М имеет направление соотв-его ей вектора

Векторные линии поля:

Описываются системой дифференциальных уравнений вида:

=

Криволинейный интеграл по замкнутому контуру L наз. Циркуляцией поля вдольL

49. Ротор и дивергенция векторного поля, их физ.Смысл и вычисление.

Ротором векторного поля наз. Вектор, обозначаемый rot и определяется формулой или

Характеризует наличие вихрей. Если ротор везде =0, то поле потенциальное

Формула для нахождения u

Где (-произв.точка обычно (0;0;0)

Физ.смысл.

Найдем ротор поля линейный скоростей твердого тела, вращающегося вокруг оси Oz с пост.угловой скоростью , т.е. ротор вектора

По определению ротора

Дивергенция характеризует наличие стоков или источников в точке

Если то т.M –источник

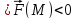то т. М- сток

50.Формула Грина и ее физич.смысл

Предположим,что в плоской области D задано векторное поле с F(с черт.)=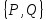причем ф.P и Q =(x,y)непрерывна по совокупности переменных +частных производных,тогда

L-контур,огр.D + выбрано направл.так,чтобы при движении по кот.область оставалась слева

51. Формула Остроградского и её физ.смысл.

dxdydz заменить на dv.S без плюса

Физ. Смысл:

поток векторного поля S через замкнутую поверхность в сторону внешней нормали равен тройному интегралу по области, ограниченной этой поверхностью, от дивергенции векторного поля S.

52. Формула Стокса и её физ.смысл

 циркуляция векторного поля S вдоль замкнутого контура равна потоку ротора векторного поля S через поверхность, натянутую на этот контур.

53. Общие понятия теории рядов. Свойства рядов. Необходимый признак сходимости числового ряда.

Где действительные или комплексные числа, называемые членами ряда,- общим членом ряда.

Ряд считается заданным, если известен общий член ряда 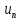, выраженный как функция его номера

Сумма первых членов ряда--й

Если последовательность частичных сумм данного ряда имеет предел S т.е.

,

то ряд сходится и S – его сумма. Записывается это следующим образом:a1 + a2 + a3 + … + a_n + … = S, или = S.(a=u)

если не существует или равен бесконечности называют расходящимся.

1. Если ряд сходится и его сумма равна S то рядгде с произвольное число, также сходится и его сумма равна сS. Если же ряд расходится и с≠0 то и ряд расходится.

2. Если сходится ряд 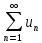и сходится ряда их суммы равнысоответственно то сходятся и ряды, причем сумма каждого равна соответственно

3. Если к ряду прибавить( или отбросить) конечное число членов, то полученный ряд и изначальный ряд сходятся или расходятся одновременно.

Необх. Признак сходимости:Если ряд сходится то его общий член

Дост. Условие расходимости если или этот предел не сущ. То ряд расходится.