3. Проверочный расчет ригеля на жесткость общую и местную устойчивость, выносливость, прочность

3.1 Расчет ригеля на жесткость

Проверку балки на жесткость ведем с помощью интеграла Мора. Считаем, что балка находится в Р — состоянии. Это состояние называют грузовым (рисунок 3.1).

Рисунок 3.1

Определяем моменты, которые возникают между точками А и В от действия силы Р на расстояниях х₁ и х₂:

(3.1)

(3.2)

где F – действующая нагрузка на балку, Н; l – пролет балки, м; x₁ и х₂ – расстояние отрезков на балке, м.

0 < х₁ < 0,8 м;

0,8 < х ₂ < 1,6м;

Рассмотрим туже балку в единичном состоянии. Теперь с балки сняты все заданные нагрузки, но в точке С приложена единичная сила F = 1 (рисунок. 3.2).

Рисунок. 3.2

Определим моменты, возникающие в результате действия единичной силы:

(3.3)

(3.4)

0 < х₁ < 0.8 м;

0.8< х₂ < 1.6 м;

Интеграл Мора имеет вид:

(3.5)

где М₁ и М_F – моменты от единичной и грузовой сил соответственно, Н∙м; ЕJ_z – жесткость балки, ЕJ_z = const.

(3.6)

где k – коэффициент, характеризующий произведение эпюр моментов, k = k₁+k₂ (т.к. два участка с различными функциями момента).

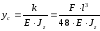(3.9)

Условие жесткости для балки имеет вид:

(3.10)

Т.е. условие жесткости выполняется.

3.2. Расчет ригеля на общую устойчивость

При нагружении балки, работающей на изгиб в плоскости наибольшей жесткости, может возникнуть явление потери общей устойчивости (рисунок 3.2).Сжатый пояс балки выпучивается в боковом направлении, и возникает кручение. Потеря общей устойчивости ригелем сопровождается возникновением значительных нормальных напряжений в сечении ригеля (визуально - изгиб).

Расчет производим по методике представленной в [1]

Рисунок 3.3.

Проверку общей устойчивости для балки производим с помощью формулы:

(3.11)

где - коэффициент снижения напряжений при потере устойчивости.

Для балок с двутавровым сечением:

(3.12)

где J_x и J_y – моменты инерции сечения балки по X и Y, м⁴ ; ψ – справочный коэффициент, для стали СтЗ ψ = 3,06-7,79; h – полная длинна балки, м.

Т.е. условие общей устойчивости выполняется.

3.3. Расчет ригеля на местную устойчивость

Потеря местной устойчивости ригелем сопровождается возникновением значительных касательных напряжений (визуально – кручение).

Потеря двутавровым ригелем местной устойчивости

Рисунок 3.4.

Проверку на местную устойчивость производим по условию:

(3.13)

где n – коэффициент запаса прочности, n = 2,4; n₀ – коэффициент запаса местной устойчивости.

(3.14)

где Q – вес перемещаемого, груза, Н; τ

h_c – высота балки, м

s_c – толщина стенки двутавровой балки, м.

Напряжения τ_кр вычисляются по следующей формуле:

(3.15)

где σТ - предел текучести, для стали ВСтЗсп = 240 МПа.

Тогда коэффициент запаса местной устойчивости составит:

Т.е. условие местной устойчивости выполняется.

Двутавр из стали СтЗ можно не укреплять ребрами жесткости, т.к. стенка под нагрузкой достигнет текучести от касательных напряжений раньше, чем потеряет устойчивость при h_c/δ_c < 90, h_c/δ_c = 120/5 = 24 < 90. Потеря местной устойчивости может происходить только у стенок и поясов. Критическими значениями гибкости для поясов балок из СтЗ является:

(3.16)

где b – ширина полки, b = 74 мм;

t – средняя толщина полки балки, t = 8.4 мм.

Т.е. условие выполняется.