23. Основы теории гидродинамического подобия. Виды подобия и основные критерии.

Геометрическое подобие, как известно из геометрии, предполагает пропорциональность сходственных размеров и равенство соответствующих углов. В гидравлике под геометрическим подобием понимается подобие тех поверхностей, которые ограничивают потоки, то есть подобие русел или каналов. При этом подобными должны быть не только русла в пределах изучаемого участка, но и непосредственноперед и за ними, так как они будут оказывать влияние на характер течения жидкости на изучаемом участке. Отношение двух сходственных размеров подобных русел назовем линейным масштабом и обозначим черезkL. Эта величина одинакова (idem) для подобных русел I и II:

.

Кинематическое подобие означает пропорциональность местных скоростей в сходственных точках и равенство углов, характеризующих направление этих скоростей:

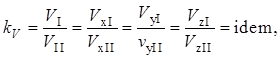
где kV – масштаб скоростей, одинаковый при кинематическом подобии.

Так как

где T – время, kT – масштаб времени.

Очевидно, что для кинематического подобия необходимо геометрическое подобие русел.

Динамическое подобие – это пропорциональность сил, действующих на сходственные объемы в кинематически подобных потоках и равенство углов, характеризующих направление этих сил.

В потоках жидкости обычно действуют разные силы: силы давления, вязкости, тяжести и др. Соблюдение этих пропорциональностей означает полное гидродинамическое подобие. Осуществить полное подобие на практике удается далеко не всегда, поэтому часто имеют дело с частичным (неполным) подобием, при котором пропорциональны только лишь основные, главные силы.

Для напорных течений в закрытых руслах, то есть для потоков в трубах, в гидромашинах и т. п., такими силами являются силы давления, вязкости и инерции. На жидкость действует также сила тяжести, но в напорных потоках ее действие проявляется через давление: pпр = p + grh, то есть она учитывается.

Силы инерции определяются произведением массы на ускорение F = ma, а их отношение в подобных потоках равно масштабу сил:

где kr – масштаб плотностей.

Таким образом, силы инерции пропорциональны плотности, квадрату скорости и размеру L во второй степени, то есть площади S:

Силы инерции примем за основу и другие силы будем сравнивать с инерционными, то есть с 

Таким образом, для гидродинамического подобия потоков необходимо, чтобы

Это отношение называют числом Ньютона и обозначают Ne.

24.Основы теории ламинарного движения(распределение касательных напряжения и скоростей, определение потерь напора)

Ламинарное движение является строго упорядоченным, слоистым течением без перемешивания жидкости.

Рис. 1.6.1. Слоистый характер потока при ламинарном течении жидкости

Так как в этом случае перемещение частиц жидкости происходит только в осевом направлении, а поперечные составляющие скорости отсутствуют, то схематически ламинарный поток можно представить в виде бесконечно большого числа бесконечно тонких, концентрично расположенных цилиндрических слоев, параллельных оси трубопровода и движущихся один внутри другого с различными скоростями, увеличивающимися в направлении от стенок к оси трубы (рис. 1.6.1).

Слои жидкости, движущиеся быстрее, увлекают за собой слои, движущиеся медленнее, и наоборот, слои, движущиеся медленнее, тормозят слои жидкости, движущиеся быстрее. Происходит как бы скольжение цилиндрического слоя, движущегося с большей скоростью, по слою, движущемуся с меньшей скоростью. При этом из-за наличия сцепления частиц жидкости друг с другом и со стенками трубы на соприкасающихся поверхностях слоев жидкости возникают силы трения, направленные параллельно оси трубы, навстречу потоку.