ЛАБОРАТОРНАЯ РАБОТА № 3

Элементы математической статистики.

1. Теоретические сведения

Математическая статистика — раздел математики, в котором изучаются методы сбора, систематизации и обработки результатов наблюдений массовых, однородных случайных явлений для выявления сущест­вующих закономерностей.

Пусть требуется изучить данную совокупность объектов отно­сительно некоторого признака.

Совокупность всех подлежащих изучению объектов или воз­можных результатов всех мыслимых наблюдений, производимых в неизменных условиях над одним объектом, называется генеральной совокупностью.

Выборочной совокупностью (выборкой) называется совокуп­ность объектов, отобранных случайным образом из генеральной сово­купности. Более строго: выборка — это последовательность незави­симых одинаково распределенных случайных величин, распределение каждой из которых совпадает с распределением генеральной случай­ной величины.

Число объектов (наблюдений) в совокупности называется ее объемом.

Пусть изучается некоторая С.В. . С этой целью над С.В.про­изводится ряд независимых опытов (наблюдений). В каждом из этих опытов величинапринимает то или иное значение.

Пусть она приняла раз значение,раз — значение, …,раз — значение. При этом— объем выборки. Значенияназываетсявариантами С.В. .

Размах выборки W − разность между максимальным и мини­мальным значениями элементов выборки: .

Операция расположения значений случайной величины (при­знака) по неубыванию называется ранжированием статистических данных. Полученная таким образом последовательность значений С.В.и, …, называется вариационным рядом.

Числа , показывающие, сколько раз встречаются вариантыв ряде наблюдений, называются частотами, а отношение их к объему выборки —относительными частотами, т.е. ,,.

Перечень вариант и соответствующих им частот или относительных частот называется статистическим распределением выборки или статистическим рядом.

Обычно, статистический ряд записывают в виде таблицы (табл.1).

Таблица 1

xi	x1	x2	...	xk
ni	n1	n2	...	nk
			...

В случае, когда число значений признака (С.В. ) велико или признак является непрерывным (т.е. когда С.В. можетпринимать любое значение в некотором интервале), составляют интервальный статистический ряд (таблица 2). Для этого весь диапазон значений С.В. отдоразбивают наинтервалов (обычно от 5 до 20) одинаковой длины, подсчитывают частоты значений выборки, попавших в интервалы. Для определения количества интервалов обычно применяется формула.

Таблица 2

Интервал			...
Середина интервала			...
Частота	n1	n2	...	nk
Относительная частота			...

Одним из способов обработки вариационного ряда является построение эмпирической функции распределения. Эмпирической (статистической) функцией распределения называется функция , определяющая для каждого значениячастость события:. Для нахождения значений эмпирической функции удобнозаписать в виде

, (1)

где — объем выборки,— число наблюдений, меньших().

Полигоном частот называют ломаную, отрезки которой соединяют точки с координатами ,,…,; полигоном относительных частот — с координатами,,…,.

Гистограммой частот (относительных частот) называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины , а высоты равны отношению— плотность частоты (— плотность относительной частоты). Площадь гистограммы частот равна объему выборки, а площадь гистограммы относительных частот равна единице.

Пусть статистическое распределение выборки объема имеет вид:

	…
	…

Выборочным средним называется среднее арифметическое всех значений выборки:

. (2)

В случае интервального статистического ряда в качестве берут середины его интервалов, а — соответствующие им частоты.

Выборочной дисперсией называется среднее арифметическое квадратов отклонений значений выборки от выборочной средней, (3)

Выборочное среднее квадратичное отклонение выборки определяется формулой .

Исправленная выборочная дисперсия — величина, определяемая по формуле

, . (4)

Величина называетсяисправленным выборочным средним квадратичным отклонением.

Статистической оценкой (или просто —оценкой )параметра теоретического распределения генеральной совокупности называют его приближенное значение, найденное по выборке. Оценка есть значение некоторой функции результатов наблюдений над случайной величиной.

Функцию результатов наблюдений (т.е. функцию выборки) называют статистикой.

К оценке любого параметра предъявляется ряд требований, которым она должна удовлетворять, чтобы быть «близкой» к истинному значению параметра.

Оценки должны удовлетворять определенным требованиям.

Несмещенной называется статистическая оценка , математическое ожидание которой равно оцениваемому параметрупри любом объёме выборки, т.е.. Если, то оценканазываетсясмещенной. Если , то оценканазываетсяасимптотически несмещенной.

Эффективной называется статистическая оценка, которая (при данном объеме выборки) имеет минимально возможную дисперсию.

Состоятельной называется статистическая оценка, которая при стремится по вероятности к оцениваемому параметру, т.е..

Статистические оценки делятся на два класса: точечные и интервальные.

Точечной называют статистическую оценку, которая определяется одним числом. Например, выборочное среднее , выборочная дисперсия и т. д.

Выборочное среднее —несмещенная и состоятельная оценка математического ожидания.

Выборочная дисперсия являетсясмещенной оценкой дисперсии.

Исправленная выборочная дисперсия —несмещенная и состоятельная оценка дисперсии.

Эмпирическая функция распределения выборки являетсянесмещенной состоятельной оценкой функции распределения случайной величины.

Точечные оценки неизвестного параметра хороши в качестве первоначальных результатов обработки наблюдений. Недостатком является то, что неизвестно с какой точностью они дают оцениваемый параметр.

Оценка неизвестного параметра называется интервальной, если она определяется двумя числами — концами интервала, покрывающего оцениваемый параметр.

Доверительным интервалом для параметра называется интервал, который покрывает неизвестный параметрс заданной надежностью, т.е.. Числоназываетсядоверительной вероятностью, а значение − уровнем значимости. На практике обычно используют уровни значимости: 0.1, 0.05, 0.01.

Доверительный интервал для математического ожидания нормально распределенной случайной величины при данном уровне значимостии известной дисперсииимеет вид

, (5)

где определяется из условия, илии

−функция Лапласа.

При неизвестной дисперсии генеральной совокупности используется формула

, (6)

где определяется с помощью таблицы значений распределения Стьюдента по данному числу степеней свободыи уровню значимости.− оценка среднего квадратического отклонения. Отметим, что при объеме выборкивместо распределения Стьюдента можно пользоваться нормальным распределением.

Под статистической гипотезой (или просто гипотезой) понимают всякое высказывание (предположение) о генеральной совокупности, проверяемое по выборке.

Статистические гипотезы делятся на гипотезы о параметрах распределения известного вида (параметрические гипотезы) и гипотезы о виде неизвестного распределения (непараметрические гипотезы).

Одну из гипотез выделяют в качестве основной (или нулевой) , а другую, являющуюся логическим отрицанием— в качествеконкурирующей (или альтернативной) гипотезы.

Процедура проверки соответствия высказанного предположения (гипотезы) с выборочными данными называется проверкой гипотезы.

Правило, по которому принимается решение принять или отклонить гипотезу , называетсястатистическим критерием (или просто критерием) проверки гипотезы .

Критерием согласия называют статистический критерий проверки гипотезы о предполагаемом законе неизвестного распределения.

Одним наиболее распространённым критерием проверки непараметрических гипотез о виде функции распределения изучаемой случайной величины является критерий(Пирсона). Данный критерий проверяет гипотезу о возможном законе распределения и применяется для разных распределений.

Схема применения критерия для проверки гипотезыН о законе распределения изучаемой случайной величины заключается в следующем:

1. Рассматриваем гипотезу Н₀ о законе распределения случайной величины (дискретной или непрерывной);

2. По выборке находим оценки инеизвестных параметров предполагаемого закона распределения;

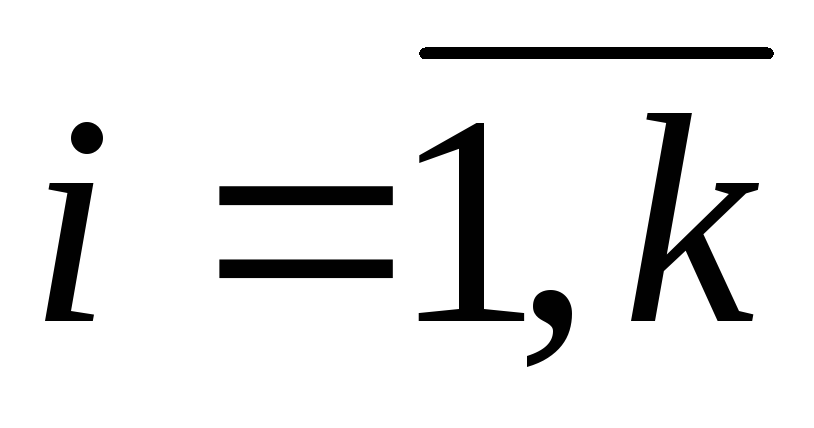3. Определяем частоты ,, с которыми встречаются в выборке каждое значение дискретной случайной величины или элементы выборки непрерывной случайной величины принадлежащие каждому из заданных интервалов;

4. Находим теоретические вероятности − для дискретной,− для непрерывной случайной величины. Для нормального закона распределения имеем

; (7)

5. Вычисляем наблюдаемое значение критерия :

; (8)

5. Контроль вычислений осуществляется равенством

. (9)

7) Принимаем статистическое решение: гипотеза Н₀ не противоречит выборке наблюдений на данном уровне значимости , если, где− число степеней свободы, а− число параметров распределения.

Если же , то гипотезаН₀ отклоняется и может быть выдвинута другая гипотеза Н₁, которая проверяется по той же схеме.